ブラックホールはなぜ見えないのか
相対性理論の計算 ブラックホールはなぜ見えないのか
ブラックホールは見えない。だがブラックホールに落下していく物体がその途中で電磁波を放射することがあるので、それを見ることでブラックホールの存在を推定することができる(ブラックホールの観測方法は他にもある)。
ところで、なぜブラックホールは見えないのだろうか。それはたいてい、ブラックホールの重力がとても強いので光もブラックホールに引かれて外に出られないからだ、といったように説明される。確かに重力のせいでブラックホールからは光もまったく出てこないし、光が出てこなければ見えないのは当たり前なので、そこは間違っていない。しかしこの説明だけでは状況を正しく思い浮かべることは難しく、誤解を招くようにも思える。
ブラックホールはもともと一般相対性理論から予言されたものである。現実のブラックホールが本当にその理論どおりになっているかはまだよくわからないが、ここでは一般相対性理論で説明されるブラックホールがどういう構造になっているから見えないのかを簡単に述べる。
1. 「見える」とはどういうことか
「なぜ見えないのか」を考える前に、「見える」とはどういうことなのかをはっきりさせておこう。
1.1 太陽の場合
例えば地球から太陽が見える場合を考えると、図1
図1 . 太陽から地球に届く光(空間的な図)
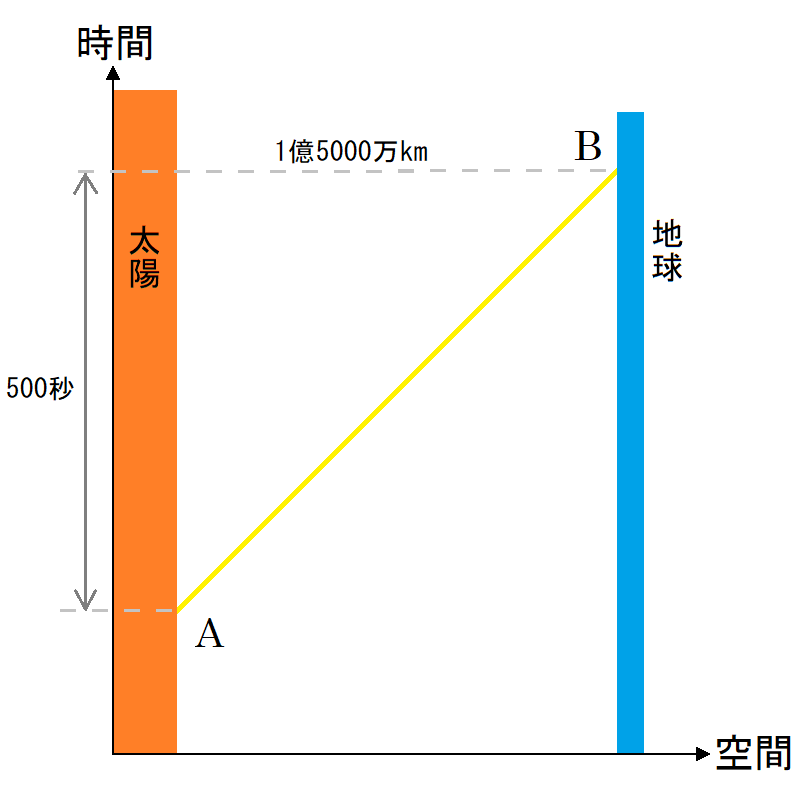
時間を意識してこの様子を描いたグラフが図2
図2 . 太陽から地球に届く光
図2
1.2 高密度の天体の場合
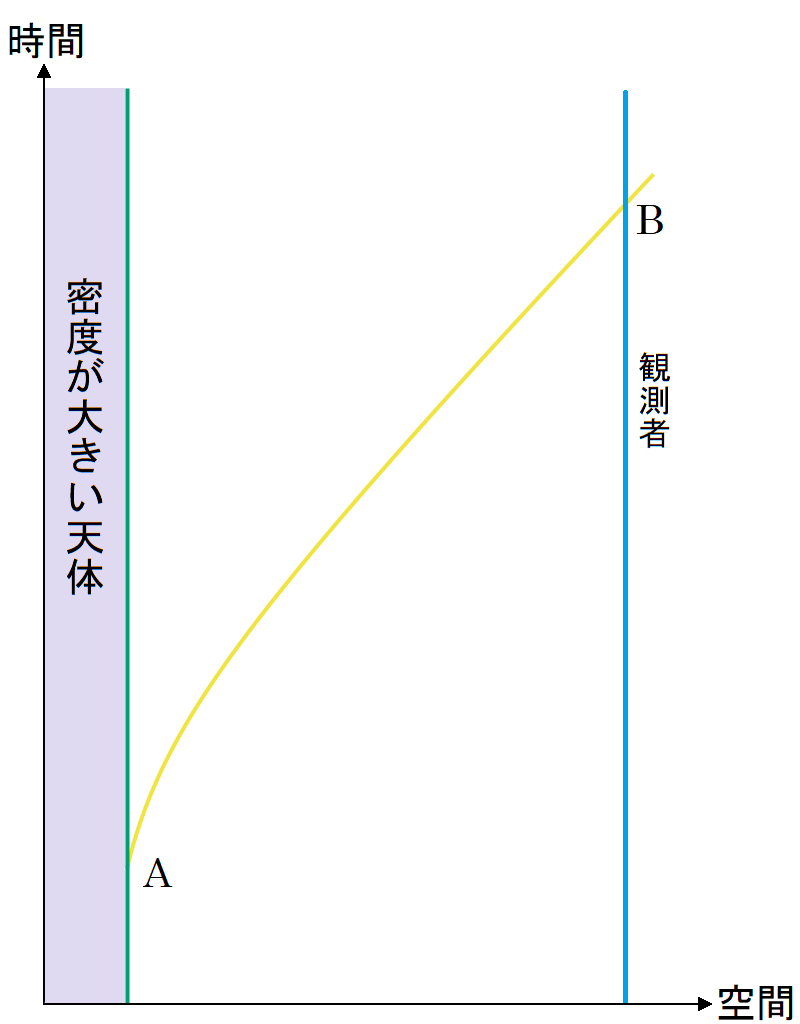
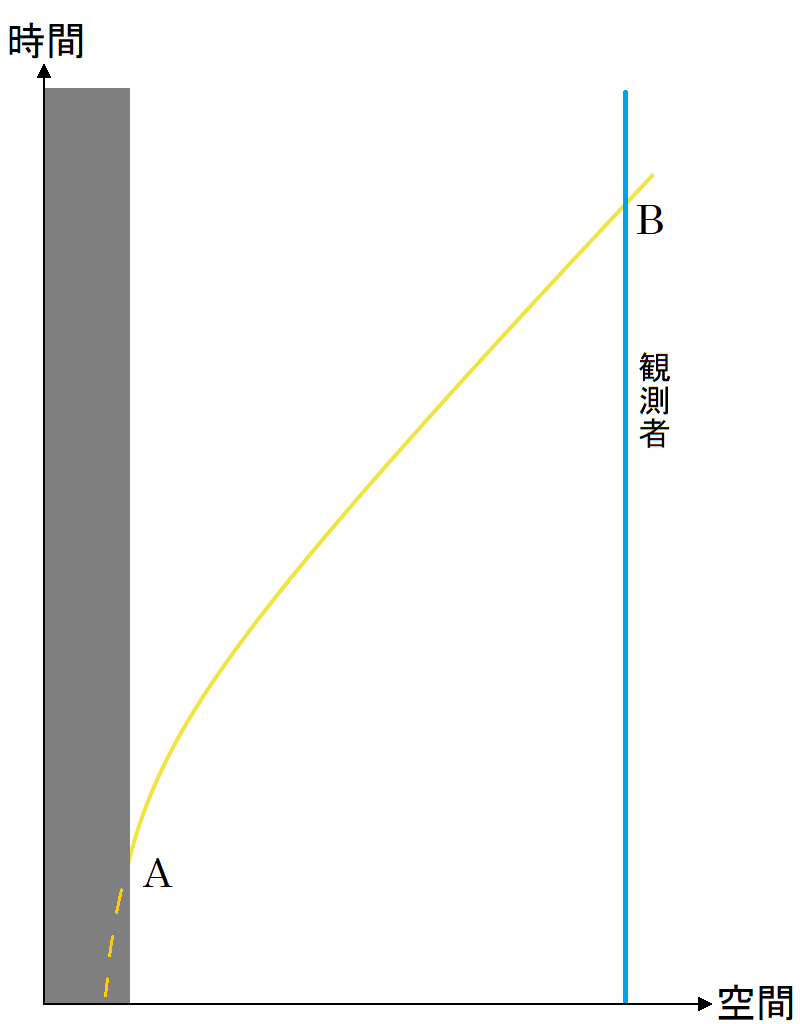
ブラックホールではないが密度がとても大きい天体(例えば中性子星)を観測する場合について、図2 図3
図3 . 高密度の天体から観測者に届く光
図3
いずれにしても、「A」で示した時刻・場所で放射された光が「B」で示した時刻・場所で観測される点は、前節の太陽の場合と同じである。
前節の図2
ではこれらが太陽や中性子星ではなくブラックホールだったらどうなるのだろうか。
2. もっとも単純な仮想的なブラックホールの場合
この節では理論的にもっとも単純な構造にモデル化されたブラックホールを考える。それは球対称・定常のブラックホールである。ここで言っている「定常」とは無限の過去から無限の未来までまったく姿を変えずに存在し続けているという意味である。現実の宇宙は138億年前にできたという説が優勢で、そうであれば無限の過去はないので、このような定常ブラックホールは現実には存在しないはずだ。しかし最初から現実的なややこしい条件を付けて考えるのは大変なので、まず単純なモデルから考えるのである。
図4 . 見えない物体(?)と観測者
さて、「光が出てこないから見えない。」と聞くと図4
そうではない。
ブラックホールに関して同様の図を描くと図5
図5 . ブラックホールと光の世界線
これを見ると、「今のところまだブラックホールの手前にある場所からの光しか届いていない」と考えることもできる。その状態が永久に続くからブラックホールは見えないのである。
(この線が事象の地平線の外側で無限に過去に伸びているように見えるのは、実は座標系の張り方が原因であって、本当はうまく座標系を張れば有限の範囲に収めることができる。その話にはホワイトホールも関係してくるが、そこまで説明すると大変なので今は触れないことにする。)
3. より現実的なブラックホールの場合
前節で考えた単純なブラックホールは無限の過去から存在するモデルであった。現実の恒星質量ブラックホールは恒星がその最期に重力崩壊して作られると考えられている。
重力崩壊の様子はおおまかに図6
図6 . 重力崩壊する星(落下する座標系)
ただしこの図は、重力崩壊する星の粒子とともに(あるいは後からそれを追って)星の中心に向かって落下していく観測者にとっての時間を基準にした図である。黄色い線は星の表面から外側に向かって放射された光の世界線である。これらの光は外部で静止している観測者に時間的に等間隔で届くようなものを描いているが、放射する側から見れば等間隔ではない。
ここで、特殊相対性理論の最初の方で勉強したことを思い出してほしい。離れた場所における「同時刻」は観測者によって異なるのであった。ここでも、落下していく観測者と外部で静止している観測者とでは同時刻が異なる。そこで図6
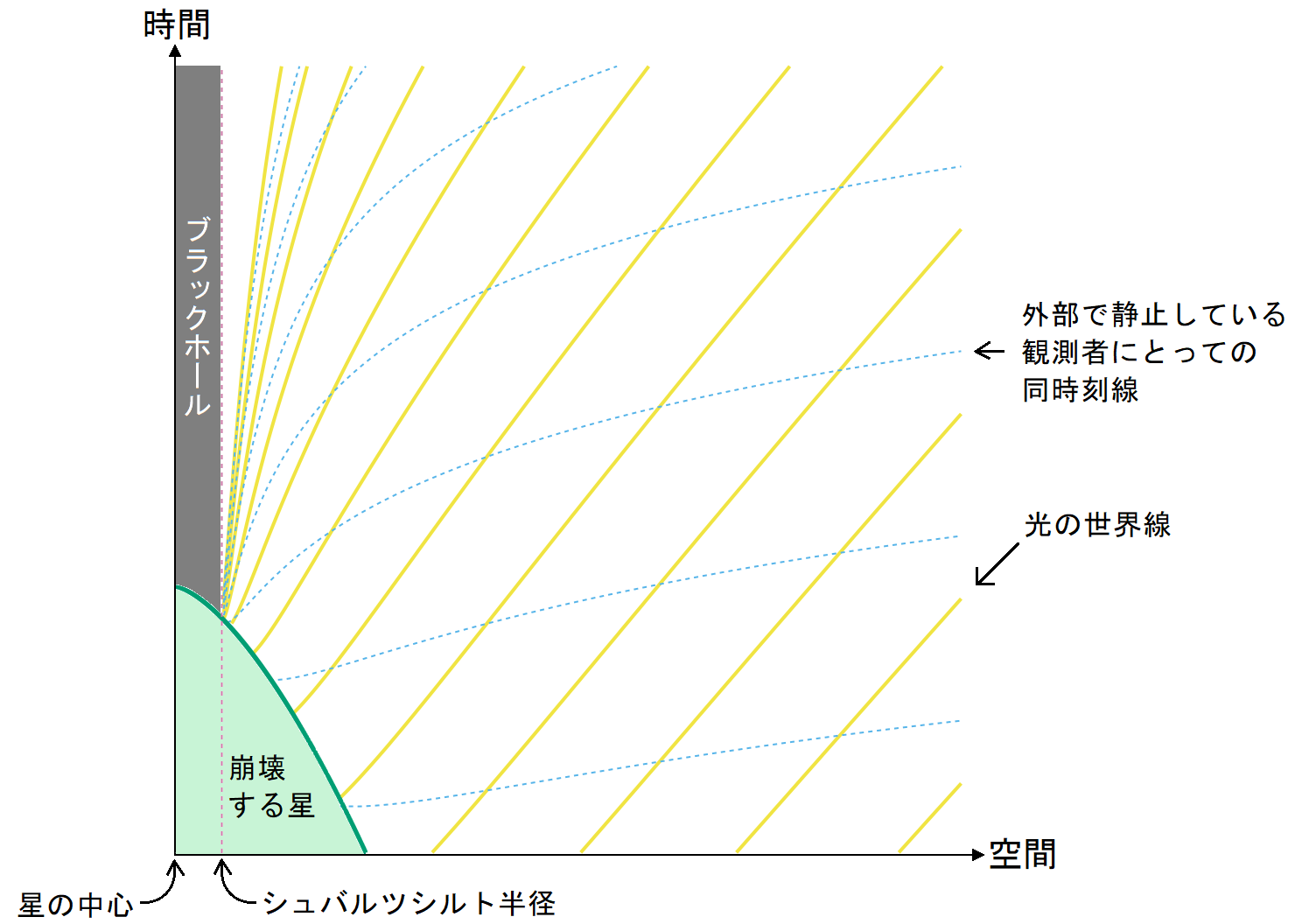
今考えたいことは、外部からこの星がどのように見える(見えない)か、であった。そこで図6 図7
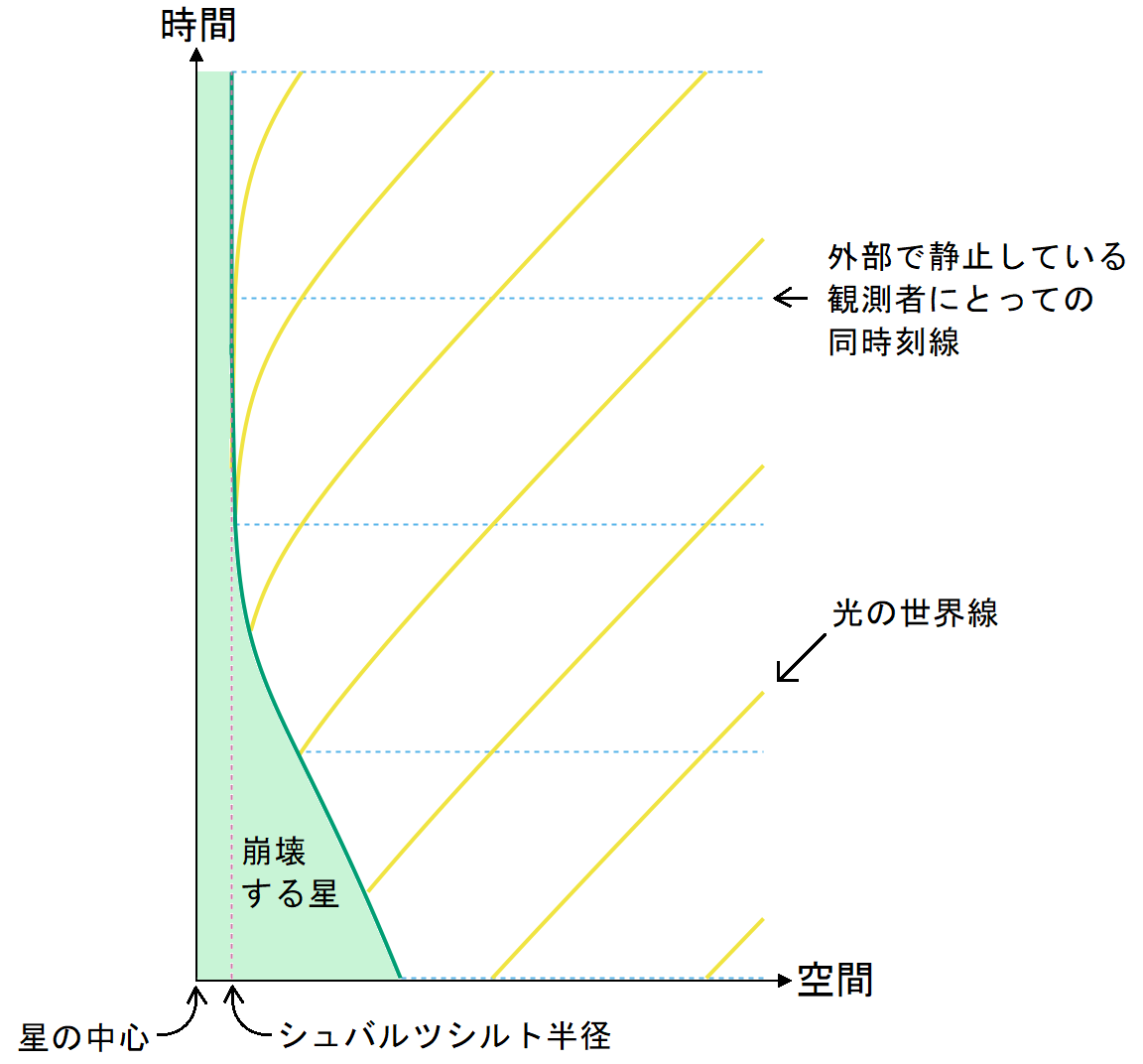
図7 . 重力崩壊する星(静止した座標系)
この座標系で考えると、星の表面はいつまで待ってもシュバルツシルト半径の内部に落ち込まず、その直前でほぼ止まってしまうのだ。図では星の表面の緑色の線とシュバルツシルト半径のピンクの破線が重なるように見えるが、厳密には緑色の線の方がほんのわずかに外側にある。その差は時間とともに指数関数的に小さくなっていくのでほとんどゼロであるが、厳密に正かゼロか負かと言われれば永久に正である。
これを外部で静止している観測者から見れば、ずっと星の表面が見え続ける……と思いたくなるかもしれないが、そうではなく無限に赤方偏移して(波長が伸ばされて)いずれ暗すぎて見えなくなってしまう。例えば星の表面の粒子が事象の地平線の内部に落ち込む直前の最後の1µ秒(100万分の1秒)間に500THzのオレンジ色の光を発したとして、外部で静止している観測者にその1µ秒分の光全体が届くには無限の時間がかかることになる。しかしその光波の山や谷は5億個しかないのだから、電磁場が5億回振動したら終わりである。その後はもう何も見えないのだ。
このように、実は外部の観測者から見ると、「ブラック」ではあるが「ホール」は永久に顔を出さない。しかし通常はこんなことをいちいち説明するのはめんどくさいから、この状態になったら一般に「ブラックホールができた。」と言っているのである。
最後に補足しておくと、ここで考えたモデルは球対称のブラックホールである。現実には重力崩壊する星は形も球対称ではないだろうし自転もしているはずなのでもっと複雑であるが、定性的な結論はたぶんそれほど大きく変わらないだろう。
4. 終わりに
2節 ・3節 でブラックホールが見えない本当の理由を説明した。
2節 のような無限の過去から(または138億年前の宇宙誕生当初から)存在する仮想的なブラックホールの場合なら、「光も出られないから見えない。」と思ってもいいだろう。しかし3節 のような星が重力崩壊してできる現実的なブラックホールの場合、まだシュバルツシルト半径の外側に星の表面が残っているがそこから来る光が無限に暗くなって見えなくなるのである。ということは事象の地平線の内側から光が外に出てこないことと、この天体が見えないこととは、直接的には関係ない。だから「光も出られないから見えない。」というのは、あまり厳密でない説明における方便なのである。
ここで1つウェブサイトを紹介しよう。コロラド大学の Andrew J. S. Hamilton 先生という人の「Falling Into a Black Hole 」というウェブサイトがある。そこではブラックホールに接近および落下していく観測者がどの方向に何を見るかをきちんと計算して、静止画および動画も使って解説されている。興味があれば見てみるといいだろう。