1. 光のドップラー効果の導出

導出は簡単である。やり方はいろいろあるが、ここでは最も直感的にわかりやすいと思われる方法を述べる。

まず場面を定義する。図1のように、観測者に固定した座標系（慣性系）を 𝐾 系とする。 𝐾 系で光速は 𝑐 である。 𝐾 系で測った光源の速度の大きさを 𝑉 とし、 𝐾 系で測った光源の速度の方向と光源から観測者に向かう方向のなす角を 𝜃 とする。また、 𝐾 系で測った光源の周期を 𝑇 とする。この 𝑇 は、 𝐾 系で時間 𝑇 が経過するごとに光源が光波の1つの山を発信するという意味だ。

光源の速度は一定とは限らないし、仮に光源が等速直線運動をしていると仮定しても 𝑉 は一定だが 𝜃 の値は刻々と変わっていく。しかしここではそのような 𝑉 や 𝜃 の変化が無視できるような短い時間について考えることとする。 𝑉 と 𝜃 は、光が観測者に到着したときの値ではなく、光が光源を出発したときの値である。

このような場面で生じるドップラー効果を2つの要因に分けて説明する。この用語に関しては4.1節で補足する。

2. 速度ベクトルとドップラー効果との関係

(3)式より、 $$\frac{{𝜆}_{𝑟}}{{𝜆}_{𝑠}}=\frac{1-\frac{𝑉\cos 𝜃}{𝑐}}{\sqrt{1-{\left(\frac{𝑉}{𝑐}\right)}^2}}=𝑎\text{(5)}$$ とおく。観測者が観測する波長は光源が発信した波長の 𝑎 倍になる、という意味である。 𝑎 が1より大きければ波長が伸び、 𝑎 が1より小さければ波長が縮む。振動数は $\frac{1}{𝑎}$ 倍になる。

一般に赤方偏移の話をするときは $\frac{{𝜆}_{𝑟}}{{𝜆}_{𝑠}}$ ではなく $𝑧=\frac{{𝜆}_{𝑟}-{𝜆}_{𝑠}}{{𝜆}_{𝑠}}$ を使うことが多い。しかしここでは 𝑧 だと後の話で式がややこしくなるので(5)式の 𝑎 ( = 𝑧 + 1) を使って話を進める。

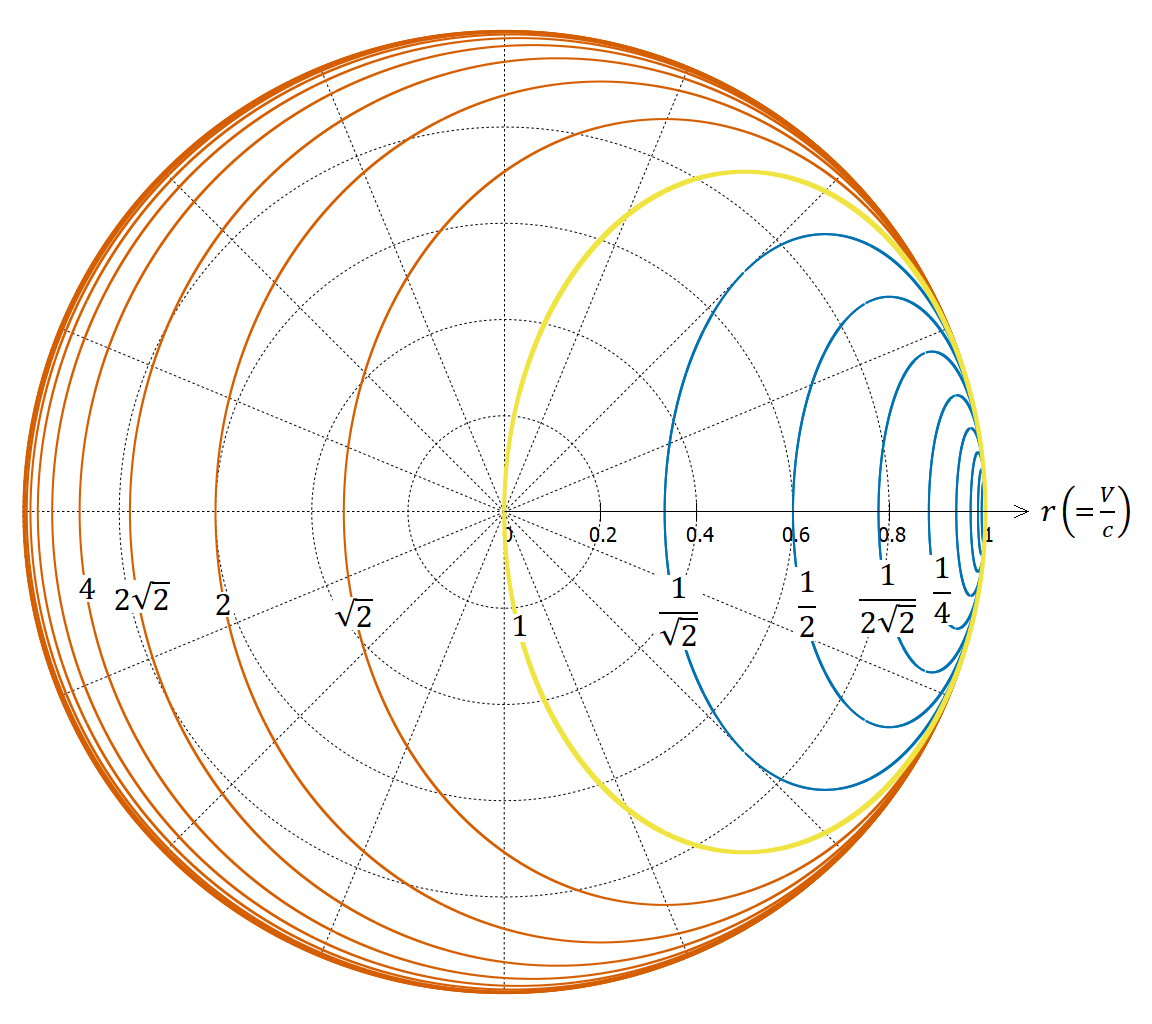
光源の速度（大きさと角度）に対応する 𝑎 の値を示したものが図2である。

動径座標は $𝑟=\frac{𝑉}{𝑐}$ 、角度座標は 𝜃 である。赤・黄・青の曲線は 𝑎 が一定となる曲線であり、 𝑎 の値が $\sqrt{2}$倍になるごとに線を引いてある。 𝑟 軸が描いてある右向きが観測者に近づく方向である。図の右半分は光源が近づく場合、左半分は光源が遠ざかる場合である。

光源の速度ベクトルが黄色い太い曲線で囲まれた部分の内側にあれば青方偏移（波長が縮んで観測されること）し、外側にあれば赤方偏移する。ちょうど黄色い線上のどこかに重なるような速度の場合は波長が変わらない。このように、近づく場合でも速度が大きくなると赤方偏移することになる。逆に言うと、大きく赤方偏移するためには方向はあまり気にせず速くなるべく遠ざかればいいが、大きく青方偏移するためには速く近づく際にしっかり方向をそろえる必要がある。

𝜃 を固定したとき 𝑟 に応じて 𝑎 がどう変化するかを調べるため、 𝑎 を 𝑟 で微分してみると、 $$\begin{array}{lll}\hfill \frac{\mathrm{\partial 𝑎}}{\mathrm{\partial 𝑟}}& =& \frac{\partial }{\mathrm{\partial 𝑟}}\frac{1-\frac{𝑉\cos 𝜃}{𝑐}}{\sqrt{1-{\left(\frac{𝑉}{𝑐}\right)}^2}}\\ & =& \frac{\partial }{\mathrm{\partial 𝑟}}\frac{1-𝑟\cos 𝜃}{\sqrt{1-{𝑟}^2}}\\ & =& (1-𝑟\cos 𝜃)\frac{\partial }{\mathrm{\partial 𝑟}}\frac{1}{\sqrt{1-{𝑟}^2}}+\frac{1}{\sqrt{1-{𝑟}^2}}\frac{\partial }{\mathrm{\partial 𝑟}}(1-𝑟\cos 𝜃)\\ & =& (1-𝑟\cos 𝜃)\frac{𝑟}{{(1-{𝑟}^2)}^{\frac{3}{2}}}+\frac{1}{{(1-{𝑟}^2)}^{\frac{1}{2}}}(-\cos 𝜃)\\ & =& \frac{(1-𝑟\cos 𝜃)𝑟+(-\cos 𝜃)(1-{𝑟}^2)}{{(1-{𝑟}^2)}^{\frac{3}{2}}}\\ & =& \frac{𝑟-{𝑟}^2\cos 𝜃-\cos 𝜃+{𝑟}^2\cos 𝜃}{{(1-{𝑟}^2)}^{\frac{3}{2}}}\\ & =& \frac{𝑟-\cos 𝜃}{{(1-{𝑟}^2)}^{\frac{3}{2}}}\end{array}$$ のようになる。これにもとづいた増減表が表1だ。

光源が観測者に近づいてくる cos 𝜃 > 0 の場合を考えると、 𝑟 = cos 𝜃 のときに 𝑎 が最小（青方偏移が最大）になり、そのときの 𝑎 の値は |sin 𝜃| である。

例えば $𝜃=\frac{𝜋}{4}$ の場合（光源が観測者に向かう方向から45°ずれた方向に運動する場合）は、 $𝑟=\frac{1}{\sqrt{2}}$ すなわち $𝑉=\frac{1}{\sqrt{2}}𝑐$ のときに 𝑎 が最小値 $\frac{1}{\sqrt{2}}$ となる。赤方偏移パラメータ 𝑧 で言えば $𝑧=\frac{1}{\sqrt{2}}-1\approx -0.29$ である。速度がこれより大きくなっても、波長がさらに短くなることはない。

図2の曲線は愚直に(5)式を $\frac{𝑉}{𝑐}(=𝑟)$ について解いて 𝜃 の関数として表したものを 𝑎 の値を変えながらグラフ描画ソフトで極座標で表示したものである。数値的には図のとおりだが、この曲線は何なのか、その計算はこうだ。

𝑎 や 𝜃 の値に応じて、 𝑟 の妥当な解の個数が0個〜2個に変化する。 𝑎 を固定して 𝜃 を動かしたらどうなるかを手動でこの式から考えるのは面倒である。次に 𝜃 について解いてみると、(6)式より $$\begin{array}{lll}\hfill 1-𝑟\cos 𝜃& =& 𝑎\sqrt{1-{𝑟}^2}\\ \hfill -𝑟\cos 𝜃& =& -1+𝑎\sqrt{1-{𝑟}^2}\\ \hfill \cos 𝜃& =& \frac{1-𝑎\sqrt{1-{𝑟}^2}}{𝑟}\\ \hfill 𝜃& =& \arccos \frac{1-𝑎\sqrt{1-{𝑟}^2}}{𝑟}\end{array}$$ となって、これもややこしい。ところでこれらをデカルト座標 (𝑥,𝑦) で表すことを考えてみる。(𝑥,𝑦) と (𝑟,𝜃) との関係は $$\{\begin{array}{l}𝑥=𝑟\cos 𝜃\\ 𝑦=𝑟\sin 𝜃\end{array}\text{(7)}$$ であり、また $${𝑟}^2={𝑥}^2+{𝑦}^2\text{(8)}$$ であるから、(6)式より、 $$\begin{array}{llll}\hfill 1-𝑟\cos 𝜃& =& 𝑎\sqrt{1-{𝑟}^2}& \text{←}\text{(6)式}\\ \hfill 1-𝑥& =& 𝑎\sqrt{1-({𝑥}^2+{𝑦}^2)}& \text{←}\text{(7)}\text{・}\text{(8)式}\text{を代入した。}\\ \hfill {(1-𝑥)}^2& =& {𝑎}^2(1-{𝑥}^2-{𝑦}^2)\text{かつ}1-𝑥\geqq 0\\ \hfill 1-2𝑥+{𝑥}^2& =& {𝑎}^2-{𝑎}^2{𝑥}^2-{𝑎}^2{𝑦}^2\text{かつ}𝑥\leqq 1\text{、以下同じなので省略}\\ \hfill ({𝑎}^2+1){𝑥}^2-2𝑥+{𝑎}^2{𝑦}^2& =& {𝑎}^2-1\\ \hfill {𝑥}^2-\frac{2}{{𝑎}^2+1}𝑥+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& \frac{{𝑎}^2-1}{{𝑎}^2+1}\\ \hfill {𝑥}^2-\frac{2}{{𝑎}^2+1}𝑥+\frac{1}{{({𝑎}^2+1)}^2}+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& \frac{{𝑎}^2-1}{{𝑎}^2+1}+\frac{1}{{({𝑎}^2+1)}^2}\\ \hfill {(𝑥-\frac{1}{{𝑎}^2+1})}^2+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& \frac{({𝑎}^2-1)({𝑎}^2+1)}{{({𝑎}^2+1)}^2}+\frac{1}{{({𝑎}^2+1)}^2}\\ \hfill {(𝑥-\frac{1}{{𝑎}^2+1})}^2+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& \frac{{𝑎}^4-1}{{({𝑎}^2+1)}^2}+\frac{1}{{({𝑎}^2+1)}^2}\\ \hfill {(𝑥-\frac{1}{{𝑎}^2+1})}^2+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& \frac{{𝑎}^4}{{({𝑎}^2+1)}^2}\\ \hfill {(𝑥-\frac{1}{{𝑎}^2+1})}^2+\frac{{𝑎}^2}{{𝑎}^2+1}{𝑦}^2& =& {\left(\frac{{𝑎}^2}{{𝑎}^2+1}\right)}^2\\ \hfill \frac{{(𝑥-\frac{1}{{𝑎}^2+1})}^2}{{\left(\frac{{𝑎}^2}{{𝑎}^2+1}\right)}^2}+\frac{{𝑦}^2}{\left(\frac{{𝑎}^2}{{𝑎}^2+1}\right)}& =& 1\end{array}$$ のようになる。見てわかるようにこれは楕円の方程式である。図2の赤・黄・青の曲線は楕円だったのだ。この図は2次元で描いているので楕円だが、現実の3次元空間では回転楕円体となる。

3. 運動量ベクトルとドップラー効果との関係

図2からわかるように、光源との相対速度が光速に近いときは速度がわずかに変わるだけでドップラー効果が大きく変わる。一方、特殊相対性理論によれば速度が光速に近いときは速度がわずかに変わるためにも運動量が大きく変わらなければならないのだった。それなら光源の運動量とドップラー効果との対応はどうなっているのだろうか。

と言っても、光源の質量（静止時に測った質量。以下同じ。）はドップラー効果と関係ないので、ここで影響するのは正しくは運動量を質量で割った4元速度の空間成分である。質量で割るのは最後にやることにして、とりあえず運動量のまま計算を進める。

特殊相対性理論によれば、光源の質量を 𝑚 とすると、光源の運動量 𝑝 は $$𝑝=\frac{𝑚𝑉}{\sqrt{1-{\left(\frac{𝑉}{𝑐}\right)}^2}}$$ である。これを $\frac{𝑉}{𝑐}$ について解くと $$\begin{array}{lll}\hfill 𝑝& =& \frac{𝑚𝑉}{\sqrt{1-{\left(\frac{𝑉}{𝑐}\right)}^2}}\\ \hfill 𝑝\sqrt{1-{\left(\frac{𝑉}{𝑐}\right)}^2}& =& 𝑚𝑉\\ \hfill {𝑝}^2(1-\frac{{𝑉}^2}{{𝑐}^2})& =& {𝑚}^2{𝑉}^2\\ \hfill (-{𝑚}^2-\frac{{𝑝}^2}{{𝑐}^2}){𝑉}^2& =& -{𝑝}^2\\ \hfill -\frac{{𝑚}^2{𝑐}^2+{𝑝}^2}{{𝑐}^2}{𝑉}^2& =& -{𝑝}^2\\ \hfill \frac{{𝑉}^2}{{𝑐}^2}& =& \frac{{𝑝}^2}{{𝑚}^2{𝑐}^2+{𝑝}^2}\\ \hfill \frac{𝑉}{𝑐}& =& \frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\end{array}$$ である。 𝑝 と 𝑉 の符号が同じだから最後の行では正の平方根を採用した。これを(5)式に代入すると、 $$\begin{array}{lll}\hfill 𝑎& =& \frac{1-\frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\cos 𝜃}{\sqrt{1-{\left(\frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\right)}^2}}\\ & =& \frac{1-\frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\cos 𝜃}{\sqrt{1-\frac{{𝑝}^2}{{𝑚}^2{𝑐}^2+{𝑝}^2}}}\\ & =& \frac{1-\frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\cos 𝜃}{\sqrt{\frac{{𝑚}^2{𝑐}^2+{𝑝}^2-{𝑝}^2}{{𝑚}^2{𝑐}^2+{𝑝}^2}}}\\ & =& \frac{1-\frac{𝑝}{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}}\cos 𝜃}{\sqrt{\frac{{𝑚}^2{𝑐}^2}{{𝑚}^2{𝑐}^2+{𝑝}^2}}}\\ & =& \frac{\sqrt{{𝑚}^2{𝑐}^2+{𝑝}^2}-𝑝\cos 𝜃}{\sqrt{{𝑚}^2{𝑐}^2}}\\ & =& \sqrt{1+{\left(\frac{𝑝}{𝑚𝑐}\right)}^2}-\frac{𝑝}{𝑚𝑐}\cos 𝜃& \text{(9)}\end{array}$$ 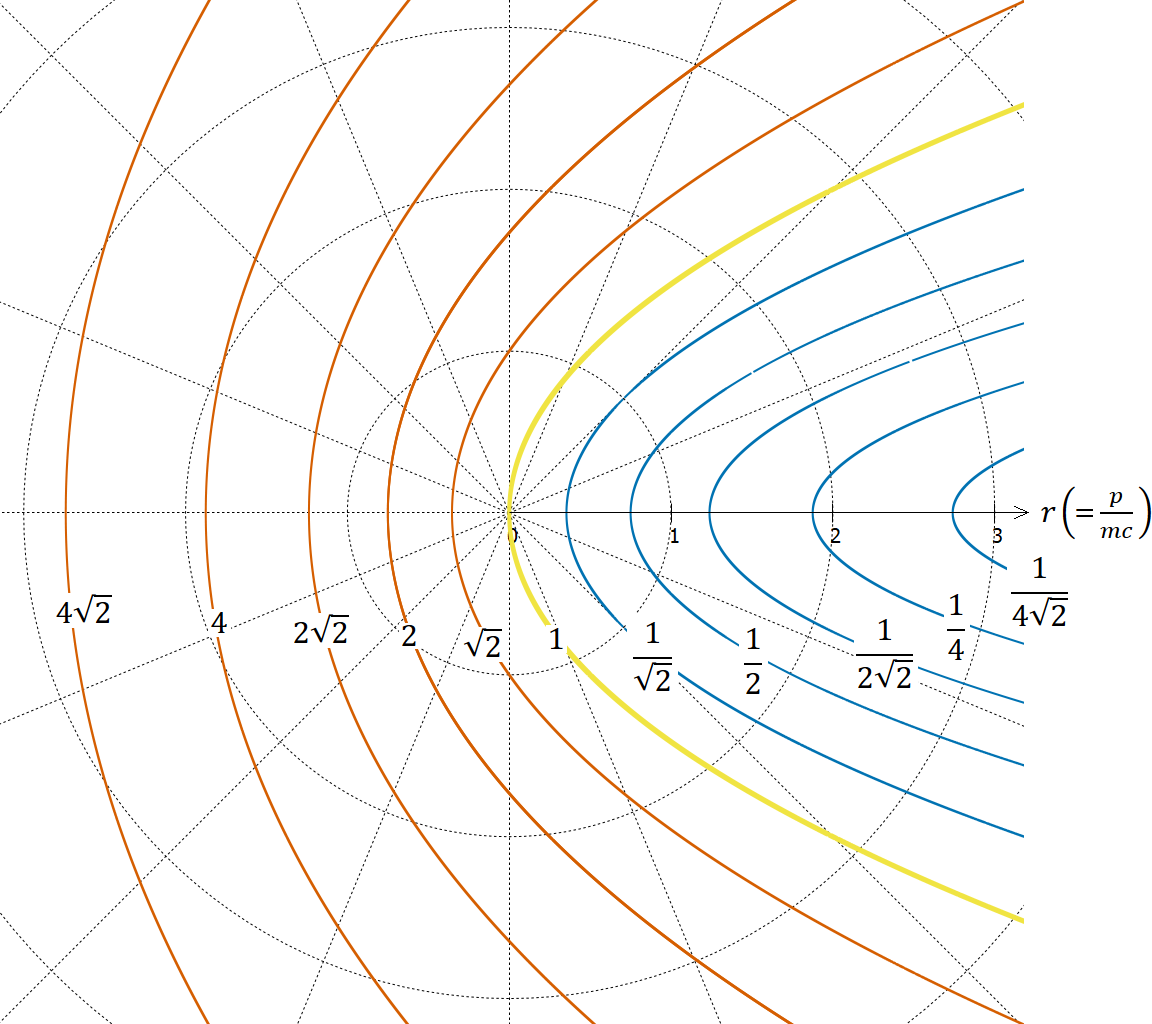のようになる。この 𝑎 の値を図示したものが図3である。

動径座標は $𝑟=\frac{𝑝}{𝑚𝑐}$ 、角度座標は 𝜃 である。 𝑟 座標の値を 𝑐 倍したもの（𝑐 倍しない流儀もある）が4元速度の空間成分、 𝑚𝑐 倍したものが運動量である。図2と同様に、赤・黄・青の曲線は 𝑎 が一定となる曲線であり、 𝑎 の値が $\sqrt{2}$倍になるごとに線を引いてある。 𝑟 軸が描いてある右向きが観測者に近づく方向である。図の右半分は光源が近づく場合、左半分は光源が遠ざかる場合である。

3次元的な速度には上限があるから図2は円内にすべての可能な状態が収まっていたが、運動量や4元速度の成分には原理的に上限がないから図3はすべての状態を表示することができない。可能な状態は図の外に無限に広がっている。 𝑝 が 𝑚𝑐 に比べてとても大きくなったときは、(9)式は次のように近似できる。

つまり方向 𝜃 が一定の場合、 𝑎 は $\frac{𝑝}{𝑚𝑐}$ にほぼ比例するようになる。ただし 𝜃 = 0 のときは第1項が0になるので第2項が効いて 𝑎 は $\frac{𝑝}{𝑚𝑐}$ にほぼ反比例するようになる。この近似が役に立つような現象が現実に存在するかどうかは知らない。

図3の曲線は愚直に(9)式を $\frac{𝑝}{𝑚𝑐}(=𝑟)$ について解いて 𝜃 の関数として表したものを 𝑎 の値を変えながらグラフ描画ソフトで極座標で表示したものである。数値的には図のとおりだが、この曲線は何なのか、その計算はこうだ。

これは sin 𝜃 が0のときは1次方程式、0でないときは2次方程式である。そこで −𝜋 ≦ 𝜃 ≦ 𝜋 とすれば、 $$\begin{array}{llll}𝜃=0\text{\hspace{0.17em}のとき}& \hfill -2𝑎𝑟-({𝑎}^2-1)& =& 0\\ & \hfill -2𝑎𝑟& =& {𝑎}^2-1\\ & \hfill 𝑟& =& -\frac{{𝑎}^2-1}{2𝑎}\\ 𝜃=\pm \mathrm{𝜋}\text{\hspace{0.17em}のとき}& \hfill 2𝑎𝑟-({𝑎}^2-1)& =& 0\\ & \hfill 2𝑎𝑟& =& {𝑎}^2-1\\ & \hfill 𝑟& =& \frac{{𝑎}^2-1}{2𝑎}\\ 0<\left|𝜃\right|<𝜋\text{\hspace{0.17em}のとき}& \hfill 𝑟& =& \frac{𝑎\cos 𝜃\pm \sqrt{{\left(𝑎\cos 𝜃\right)}^2+{\sin }^2𝜃({𝑎}^2-1)}}{{\sin }^2𝜃}\\ & \hfill & =& \frac{𝑎\cos 𝜃\pm \sqrt{{𝑎}^2{\cos }^2𝜃+{𝑎}^2{\sin }^2𝜃-{\sin }^2𝜃}}{{\sin }^2𝜃}\\ & \hfill & =& \frac{𝑎\cos 𝜃\pm \sqrt{{𝑎}^2-{\sin }^2𝜃}}{{\sin }^2𝜃}\end{array}$$ である。𝑎 や 𝜃 の値に応じて、 𝑟 の妥当な解の個数が0個〜2個に変化する。 𝑎 を固定して 𝜃 を動かしたらどうなるかを手動でこの式から考えるのは面倒である。次に 𝜃 について解いてみると、(10)式より $$\begin{array}{lll}\hfill 𝑟\cos 𝜃+𝑎& =& \sqrt{1+{𝑟}^2}\\ \hfill 𝑟\cos 𝜃& =& \sqrt{1+{𝑟}^2}-𝑎\\ \hfill \cos 𝜃& =& \frac{\sqrt{1+{𝑟}^2}-𝑎}{𝑟}\\ \hfill 𝜃& =& \arccos \frac{\sqrt{1+{𝑟}^2}-𝑎}{𝑟}\end{array}$$ となって、これもややこしい。ところでこれらをデカルト座標 (𝑥,𝑦) で表すことを考えてみる。(𝑥,𝑦) と (𝑟,𝜃) との関係は(7)・(8)式であるから、(10)式より、 $$\begin{array}{llll}\hfill 𝑟\cos 𝜃+𝑎& =& \sqrt{1+{𝑟}^2}& \text{←}\text{(10)式}\\ \hfill 𝑥+𝑎& =& \sqrt{1+{𝑥}^2+{𝑦}^2}& \text{←}\text{(7)}\text{・}\text{(8)式}\text{を代入した。}\\ \hfill {𝑥}^2+2𝑎𝑥+{𝑎}^2& =& 1+{𝑥}^2+{𝑦}^2\text{かつ}𝑥+𝑎\geqq 0\\ \hfill 2𝑎𝑥& =& {𝑦}^2-{𝑎}^2+1\text{かつ}𝑥\geqq -𝑎\text{、以下同じなので省略}\\ \hfill 𝑥& =& \frac{{𝑦}^2}{2𝑎}-\frac{{𝑎}^2-1}{2𝑎}\end{array}$$ のようになる。見てわかるようにこれは放物線の方程式である。図3の赤・黄・青の曲線は放物線だったのだ。

4. 用語について