5. 紛らわしい例
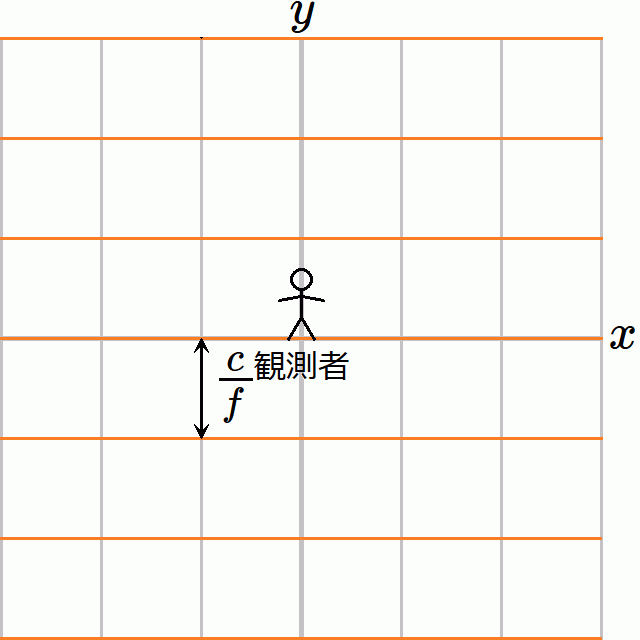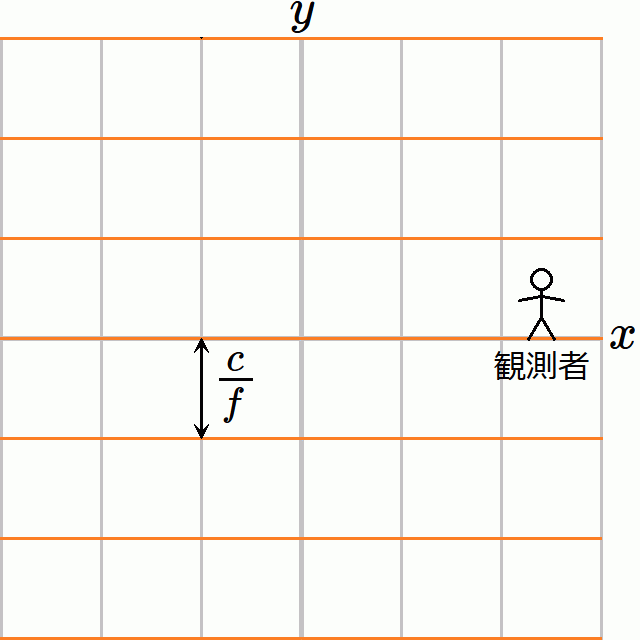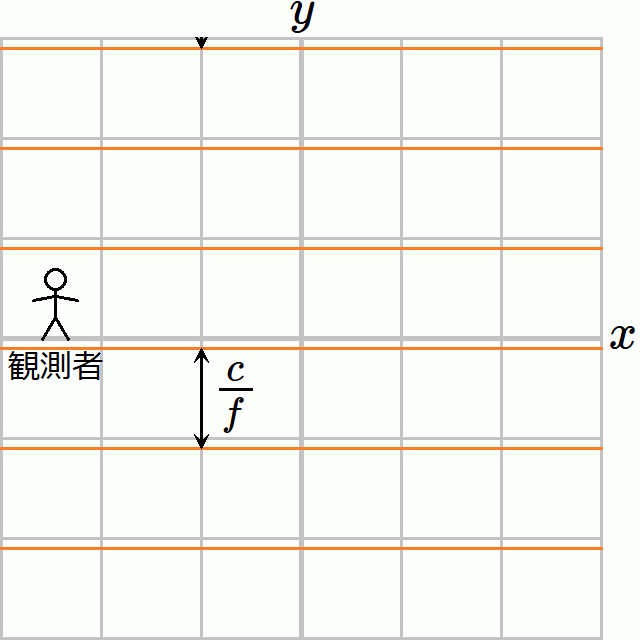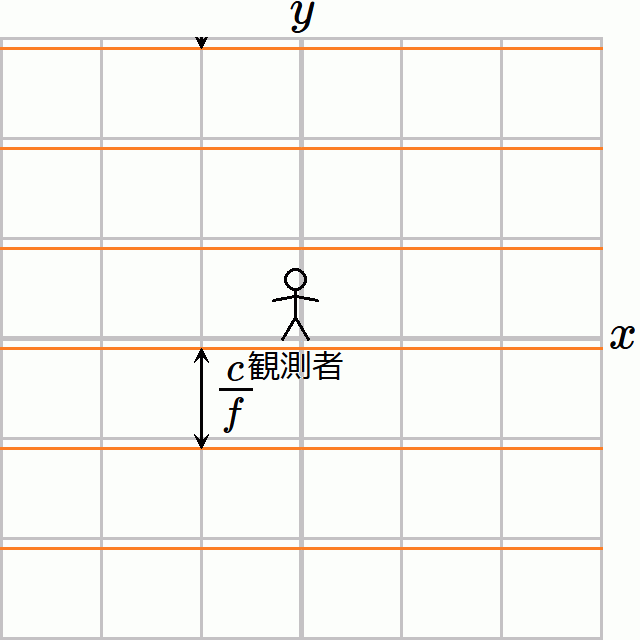
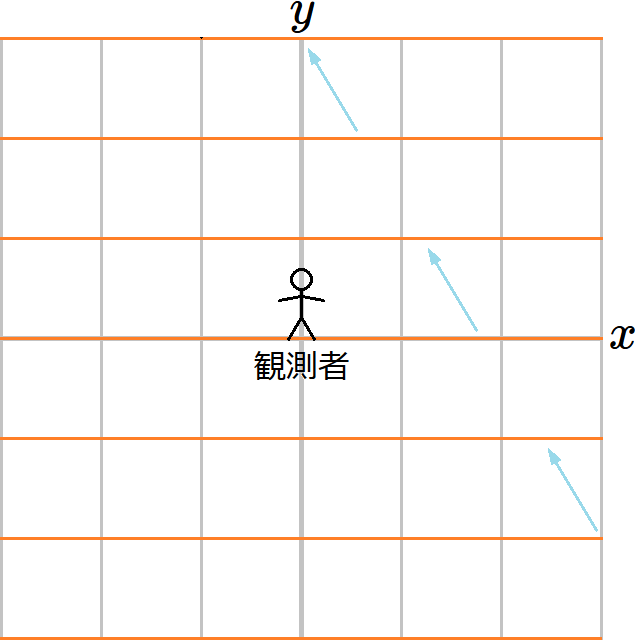
図4のような状況を想定しよう。
時空は平坦だとする。慣性系である 𝐾₁ 系で、真空中を振動数 𝑓 の光の平面波が 𝑦 軸正方向に進んでいる。したがって波長は である。図のオレンジ色の線が波面である。光源はこの図では見えないが、図の下の方の十分離れたところで静止しているものとする。
観測者は 𝑥 軸上を正方向に一定の速度 𝑉 で移動している。これは光の進行方向に対して直交する方向である。このとき観測者が観測する光の振動数はいくつか。
5.1 基本に立ち返った計算
𝐾₁ 系で見ている限り、時間 が経過するごとに観測者が1波長を観測するように見える。しかし観測者は動いているので時間が遅れる。𝐾₁ 系で時間 𝑇 が経過したとき、観測者にとってはより短い時間 しか経過していない。だから観測者が観測する振動数 𝑓′ は である。これは元の振動数 𝑓 より大きい。すなわち青方偏移する。以上でこの例の計算は終わりである。
ところで前のページの1.2節で算出した(2)・(4)式では、真横に動くとき、横ドップラー効果により振動数が 倍になって赤方偏移するのであった。それとの関係はどうなっているのだろう。
これは慣れないと間違えそうになるが、前のページでは観測者は静止していた(図1)。そのような座標系で光源の運動方向と光の進行方向のなす角が 𝜃 なのであった。そしてそこでは のことを「真横」と言った。それに対して今の図4の例では、光源が静止している座標系 𝐾₁ 系で観測者の運動方向と光の進行方向が直交しているのである。ではこの状況を(4)式に当てはめると 𝜃 がどうなるのか、ちゃんとつじつまが合っているのかを確認しよう。
そのためには、まず観測者が静止する座標系に座標変換することを考える。
5.2 (寄り道)ガリレイ変換
ここで寄り道して、非相対論的にガリレイ変換ではどうなるかを考えてみると、図5のようになる。
変換自体は何も難しいことはなく、等位相面の見た目は変換前とまったく変わらないし振動数も変わらない。ただし“エーテル”が 𝑥 方向に速度 −𝑉 で動いていることになるので光の進行方向が水色矢印のように斜めになっており(光行差)、等位相面に垂直でない方向に速度 で進行している。この状況をこの座標系で説明しようとすると面倒であるので、ここでは眺めるだけにとどめる。
𝑉 が 𝑐 に比べて十分に小さければガリレイ変換でも良いが、𝑉 が 𝑐 に対して無視できない大きさになると、ガリレイ変換は現実とのずれが大きくなるはずである。
寄り道は終了。
5.3 ローレンツ変換
今から相対論的にローレンツ変換を考える。
この先同じ式を何度も何度も書くのはめんどくさいので、 、 と置く。
観測者に固定した座標系を 𝐾₁′ 系とする。 𝐾₁′ 系の変数は ′ をつけて表すことにする。この場合のローレンツ変換は であり、逆変換は である。
さて、これから2つの方法で 𝐾₁′ 系における光の進行方向を求める。電磁場をローレンツ変換する方法と光子をローレンツ変換する方法である。当然ながらどちらを使っても結果は一致する。
問題の光の方程式をまず 𝐾₁ 系で記述する。簡単のため、静電場・静磁場は存在しないこととし、電場は 𝑥 成分のみの正弦波とし、 𝑧 成分は0とする。光は 𝑦 方向に進んでいるから電磁場の 𝑦 成分はもともと0である。そうすると磁場は 𝑧 成分のみが0でないことになる。したがって電場 𝑬 と磁場 𝑩 の成分は、
のように表される。 𝐸₀ は電場の振幅でありここでは定数である。(14)式は、振動数が 𝑓 (角振動数が 2𝜋𝑓)であり 𝑦 = 一定 の面が等位相面であるような波を表している。ポインティングベクトル 𝑺 を計算してみると
であり、確かに 𝑦 の正方向を向いている。ただし 𝐞𝑥, 𝐞𝑦, 𝐞𝑧 はそれぞれ 𝑥, 𝑦, 𝑧 方向の単位ベクトルであり 𝜇₀ は真空の透磁率である。 では 𝐾₁′ 系から見たらどうなるのだろうか。それを知りたければ単に(14)式をローレンツ変換すればよい。電磁場のローレンツ変換については「電磁場のローレンツ変換を幾何学的に理解する。」の記事で軽く説明してある。今、 𝐾₁ 系に対する 𝐾₁′ 系の相対速度は 𝑥 方向に 𝑉 だから、変換式は
である。 𝑥 成分は変わらず、 𝑦 成分・ 𝑧 成分は電場と磁場が入り混じる。また、(15)式にはあからさまに書いていないが位相を表す式の中の座標の表現が 𝐾₁′ 系のものに変わる。この変換はドップラー効果に限らず基本的な電磁場のローレンツ変換の変換式である。 そこで(15)式に(14)式を代入し、さらに位相のところに(13)式を代入すると、
のようになる。これらの式は、振動数が 𝛾𝑓 (角振動数が 2𝜋𝛾𝑓)であり
の面が等位相面であるような波を表している。5.1節で計算したのと同じく振動数が 𝛾 倍になった。ポインティングベクトルは
である。以上より光の進行方向は
であり、等位相面と直交していることがわかる。 𝐾₁ 系で、個々の光子がいつどこを飛んでいるか私はよく知らないが、ここでは 𝑦 軸上を正方向に進み時刻 𝑡 = 0 に原点を通る光子を考える。その運動は
で表される。 𝐾₁′ 系にローレンツ変換するため、(13)式を代入すると、
のようになる。これらを𝑥′, 𝑦′, 𝑧′ について解き、
を使うと、
となる。ここから光子が進む方向が
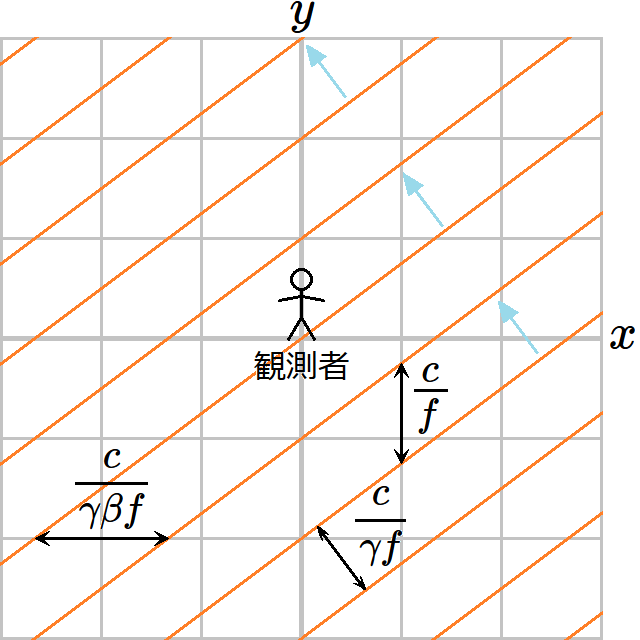
であることがわかる。今は空間は一様であるから、いつでもどこでも方向はこれと同じである。 ローレンツ変換した 𝐾₁′ 系の状況が図6である。2つの方法で求めた光の進行方向はいずれも
である。この方向を水色矢印で図示した。この矢印と等位相面は直交する。波長は
である。 𝑦 方向に平行移動したときに位相が1周する距離(位相が2𝜋変わる距離)は 𝐾₁ 系での値と同じで
である。 5.2節のガリレイ変換と異なり、電磁波の進行方向と等位相面が直交しているので、ややこしいことを考えなくて済む。ローレンツ変換は電磁波の媒質としての電磁場が誰から見ても静止して見える変換なのだから当たり前だ。電磁場のローレンツ変換
光子のローレンツ変換
ローレンツ変換の結果
5.4 計算式の比較
(4)式および図1では光源の運動方向と光の進行方向のなす角が 𝜃 であった。今、光源は 𝐾₁ 系で静止しているので、 𝐾₁′ 系から見た光源の速度は 𝑥 の負方向に 𝑉 である。光の進行方向は 𝐾₁′ 系で である。
ここで の大きさを計算してみると、 であり、その 𝑥 成分が −𝛽 であることから、 cos 𝜃 = 𝛽 がわかる。これを(4)式に代入してみると、 となって、(11)式と同じ意味の式になる(使っている記号が少し異なるが)。以上でつじつまが合っていることが確認できた。