第2章 電磁場のローレンツ変換の幾何学的モデル
ここでは電磁場のローレンツ変換を扱うが、大前提としてここで扱う電磁場は一様・定常であることとする。もし一様・定常でない電磁場を扱いたいときは、すごく狭い場所のすごく短い時間だけを考えればほぼ一様・定常と近似することができるので、そのようにして時空間を細かく区切って考えることにすればよい。
2.1 よくある3次元的なモデル
電磁場のローレンツ変換を表す(14)〜(17)式をもう一度書いておく。 𝐾 系に対する 𝐾′ 系の相対速度を 𝒗 とする。 𝐾 系における電場・磁場を 𝑬, 𝑩 、 𝐾′ 系における電場・磁場を 𝑬′, 𝑩′ とし、 𝒗 に平行なベクトルを 、垂直なベクトルを で表すと、 である。
この状況はしばしば次のような3次元的なモデルで説明される。すなわち、 𝒗 に垂直な電気力線どうしはローレンツ収縮によって間隔が 倍になる(狭くなる)ため電気力線の密度が大きくなるので 𝒗 に垂直な電場の大きさは 倍に大きくなり、 𝒗 に平行な電気力線はローレンツ収縮しても間隔は変わらないから密度も変わらず 𝒗 に平行な電場の大きさは変わらない、というものである。磁場についても同様だ。このようにして(15)・(17)式の右辺の分子の第1項および(14)・(16)式を説明することができる。
それはそれで結構なのだが、(15)・(17)式の右辺の分子の第2項、すなわち 𝑩⟂ が 𝑬′⟂ に混じったり 𝑬⟂ が 𝑩′⟂ に混じったりする現象が表現できないのが不満である。そこで次節ではそのような現象にも対応できるモデルを作ってみよう。
2.2 ポテンシャルを使った4次元的なモデル
電場と磁場は(3)式のように1つの2階のテンソルの成分になっている。2階のテンソルは1つの成分を指定するために2つの方向を定めなければならない。そのようなややこしいものを図形的に簡単に表すのは無理がある。だが4元ポテンシャル 𝐴𝜇 であればベクトル(1階のテンソル)なので、まだなんとかなりそうであるから、以下では 𝐴𝜇 に基づいた図を使って電磁場を表現してみる。
電磁場テンソルの空間‐空間成分と4元ポテンシャルとの関係は、当たり前だが3次元的な電磁気学で出てきた と同じで、例えば磁場の 𝑧 成分なら である。この右辺は4元ポテンシャル 𝐴𝜇 の渦の 𝑥‐𝑦 平面に関する成分を表している。そこで磁場の 𝑧 成分を表すのに 𝑧 方向を向いた矢印(磁束線)ではなく、 𝑥‐𝑦 平面内でループする矢印を使って表したものが図1だ。本当はいたるところにループが存在するのだが無限個のループを描くことはできないので4個だけ描いてある。磁石の運動を考えるような応用的な場面では磁束線が便利であるが、磁荷ではなく運動する荷電粒子を扱うならこの方が合理的である。磁場の 𝑧 成分というのは、 𝑦 軸方向に運動する荷電粒子の電荷×速度とその荷電粒子が 𝑥 軸方向に受ける力との比例係数であるから、関係する方向は 𝑦 と 𝑥 であり、 𝑧 軸方向は関係ないのだ。
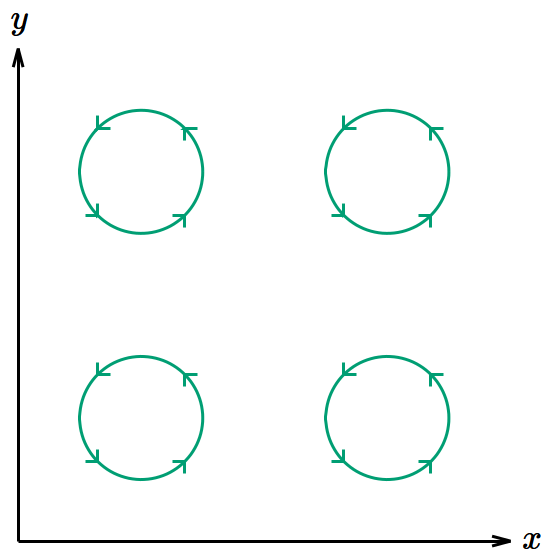
図1は 𝑥‐𝑦 平面上 のみに矢印を描いているが、一様・定常な磁場なら時空内のどこでも同じ状況になっているはずだ。今は3次元空間ではなく4次元時空を考えているから、 𝑧 方向に加えて 𝑐𝑡 方向も考えなければならない。そこで矢印を 𝑧 方向や 𝑐𝑡 方向に平行移動させて、円柱のように表示したのが図2である。これはベクトル解析で出てくる渦管である(4次元のベクトル場でも渦管と呼んでいいのかどうか知らないが)。本当はいたるところに渦管が存在するのだが無限個の渦管を描くことはできないので2個だけ描いてある。この4次元の渦管みたいなものがポテンシャルの渦を表す。そして単位面積当たりに 𝑥‐𝑦 平面と交差する渦管の数が磁場の 𝑧 成分に比例する(あるいは同じことだが、 𝑥‐𝑦 平面によって切り取られる渦管の断面積が磁場の 𝑧 成分に反比例する)ことにしておく。同様に磁場の 𝑥 成分は 𝑦‐𝑧 平面と、 𝑦 成分は 𝑧‐𝑥 平面と交差する渦管で表す。
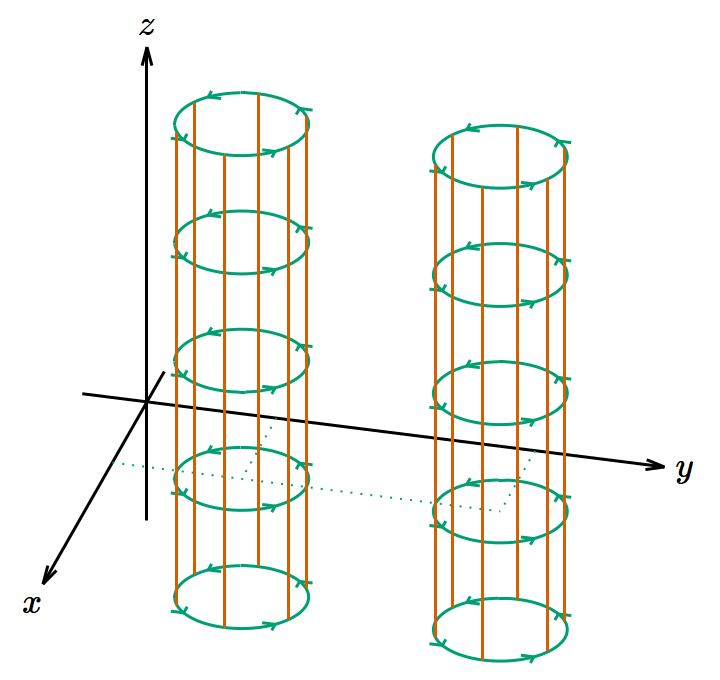
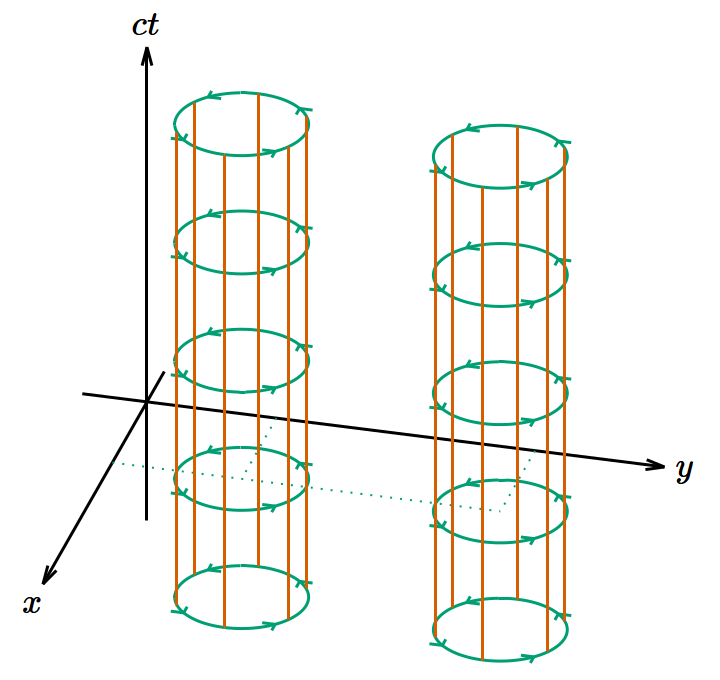
図2. 𝑧 方向の磁場を表す4次元のモデル。2次元の画面に4次元の図はまともに描けないので、第1の図では 𝑐𝑡 軸を省略し、第2の図では 𝑧 軸を省略して、それぞれ3つの次元のみを表示してある。 𝑥‐𝑦 平面内に渦があり、 𝑧‐𝑐𝑡 平面が渦線方向である。
渦の向きと磁場の符号との関係は、次のように理解すればよい。すなわち荷電粒子が空間内を動くと渦管に正面衝突し、その場所における矢印の方向(ただし負電荷の場合は逆方向)に力を受ける、ということにしておくのだ。その際に荷電粒子が渦管の内部に入る状況は考えないこととする。
電場も磁場と同様の考え方でモデルを図示することができる。例えば電場の 𝑧 成分(を光速で割ったもの)は である。磁場のときと同じように考えれば、この右辺は4元ポテンシャル 𝐴𝜇 の渦の 𝑧‐𝑐𝑡 平面に関する成分である。よって渦管のモデルは図3のようになる。同様に電場の 𝑥 成分は 𝑥‐𝑐𝑡 平面と、 𝑦 成分は 𝑦‐𝑐𝑡 平面と交差する渦管で表す。
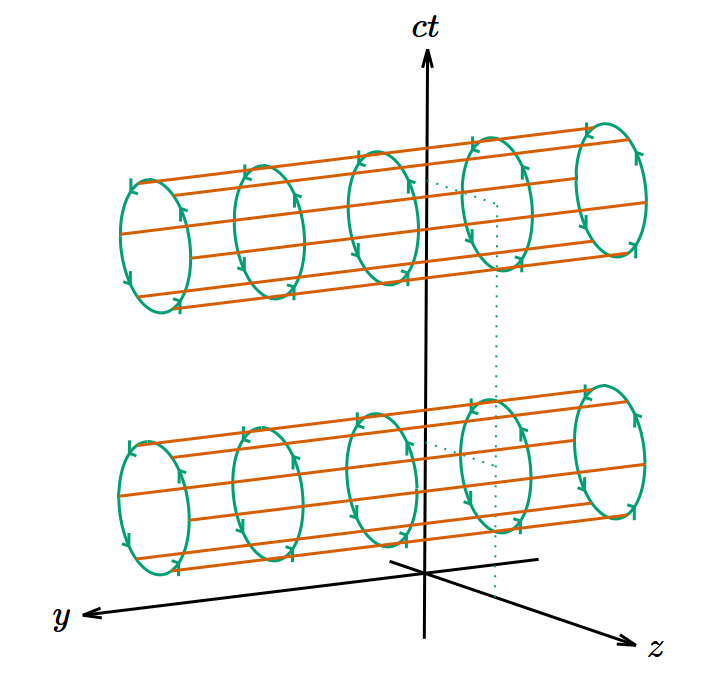
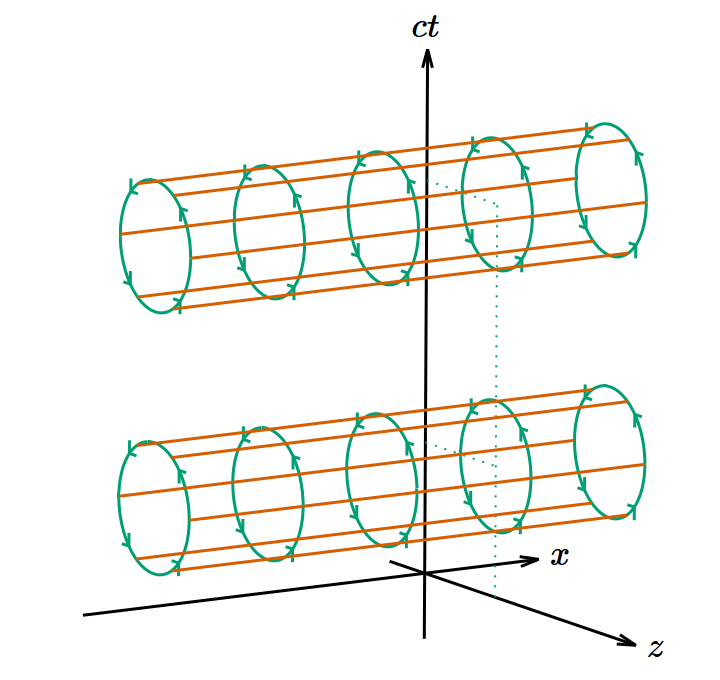
図3. 𝑧 方向の電場を表す4次元のモデル。2次元の画面に4次元の図はまともに描けないので、第1の図では 𝑥 軸を省略し、第2の図では 𝑦 軸を省略して、それぞれ3つの次元のみを表示してある。 𝑧‐𝑐𝑡 平面内に渦があり、 𝑥‐𝑦 平面が渦線方向である。
荷電粒子が受ける力については、3次元的に静止した粒子は4次元時空内を 𝑐𝑡 方向に動いていることになっているから図3の渦管にぶつかると(正電荷なら) 𝑧 軸正方向の力を受けることになり、先ほどの磁場のときの話と整合している。ところで力の 𝑐𝑡 軸方向の成分(仕事率を光速で割ったもの)を同様に考える場合には一点注意が必要だ。それはこのモデルで出てくる力は4元力の(反変成分ではなく)共変成分であるから第0成分(時間成分)の符号が普通の仕事率の符号と逆になってしまうのだ。気になる人は自分でよく考えてみてほしい。気にならない人はそこまで気にしなくてよい。
以上のように磁場と電場はともに4元ポテンシャル 𝐴𝜇 の渦で表すことができる。我々は 𝐴𝜇 の渦成分のうち、時間軸に平行な平面内の成分を電場だと認識し、時間軸に垂直な平面内の成分を磁場だと認識しているわけである。ただし 𝐴𝜇 は4次元のベクトル場だから、3次元のベクトル場の渦のような単純なものではなく、もっと複雑な状況になっていることには気を付けなければならない。
2.3 ポテンシャルを使ったモデルのローレンツ変換
さっきまで気軽に「ローレンツ変換」と言ってきたが、それは厳密には「ローレンツブースト変換」のことである。正式にはローレンツ変換の中に(3次元空間部分の)回転変換も含まれる。この節では回転変換とローレンツブースト変換を合わせた正式な意味でのローレンツ変換を扱う。
2.3.1 回転変換
最初から時間軸に関わる座標変換が登場すると難しいので、先に3次元空間内の回転変換をやって、このモデルに慣れておこう。ここでは例として、K系に対して 𝑥‐𝑦 平面内で角度 𝜃 だけ回転したK″系への変換を扱う。念のために言っておくが、K″系はK系に対してある角度を保って静止しているのであり、ぐるぐると回転運動をしているわけではない。
回転面に平行な磁場
回転面に平行な磁場の例として 𝐵𝑥 > 0, 𝐵𝑦 = 𝐵𝑧 = 0 とする。また、電場は0とする。このときK系とK″系から見たポテンシャルの渦は図4のようになる。
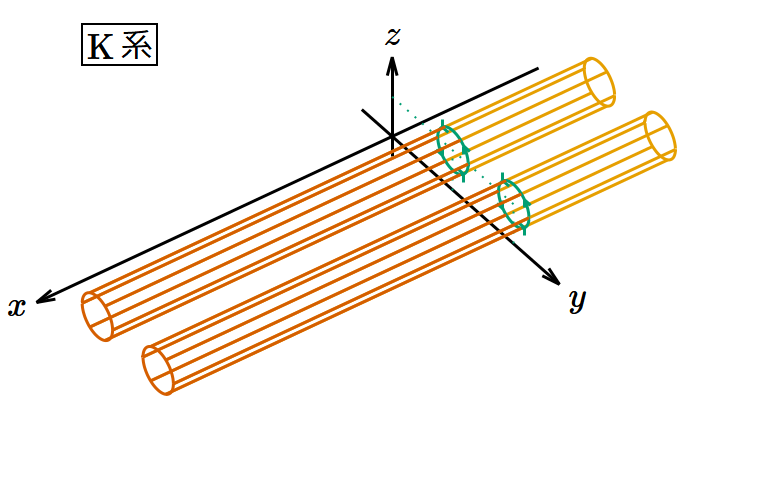
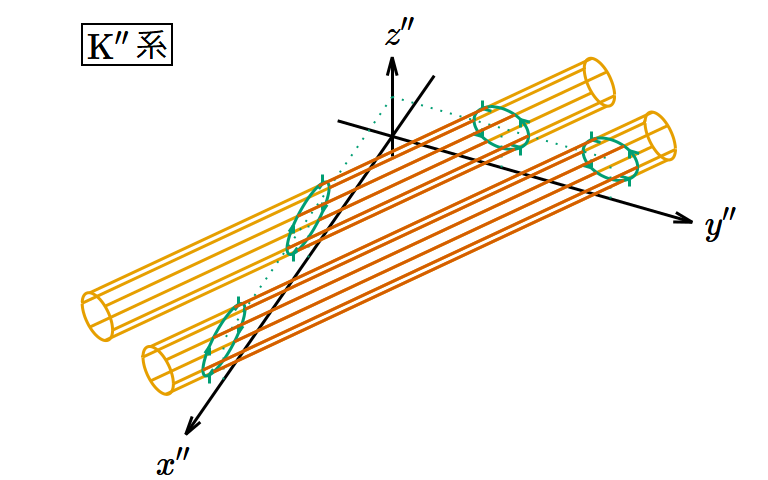
図4. 磁場の回転変換。 𝑐𝑡 軸を省略し、3つの次元のみを表示してある。 𝑐𝑡 方向に平行移動しても状況は同じである。
K系では渦管が 𝑦‐𝑧 平面と垂直に交差しているのに対し、K″系では渦管が 𝑦″‐𝑧″ 平面および 𝑧″‐𝑥″ 平面と斜めに交差している。 𝑦″‐𝑧″ 平面上で見た渦管の密度を考えると、 𝑦″ 方向の間隔は 𝑦 方向の間隔の 倍、 𝑧″ 方向の間隔は 𝑧 方向の間隔と同じだから、密度は 𝑦‐𝑧 平面上の密度の cos 𝜃 倍になる。同様に 𝑧″‐𝑥″ 平面上で見た渦管の密度は 𝑦‐𝑧 平面上の密度の sin 𝜃 倍になるが、よく見ると渦の向きが負になっていることがわかる。周知のように 𝐵″𝑥 = 𝐵𝑥 cos 𝜃 , 𝐵″𝑦 = −𝐵𝑥 sin 𝜃 であるから、これはちゃんとつじつまが合っている。
回転面に平行な電場
回転面に平行な電場の例として 𝐸𝑥 > 0, 𝐸𝑦 = 𝐸𝑧 = 0 とする。また、磁場は0とする。このときK系とK″系から見たポテンシャルの渦は図5のようになる。なぜ渦管を表す円柱の軸が 𝑦 軸なのかと疑問に思うかもしれないが、そうではなく円柱の軸は 𝑦‐𝑧 平面であり、図では 𝑧 軸を省略しているから円柱の軸をなす 𝑦‐𝑧 平面のうち 𝑦 軸の部分だけが見えているのだ。
図5. 電場の回転変換。 𝑧 軸を省略し、3つの次元のみを表示してある。 𝑧 方向に平行移動しても状況は同じである。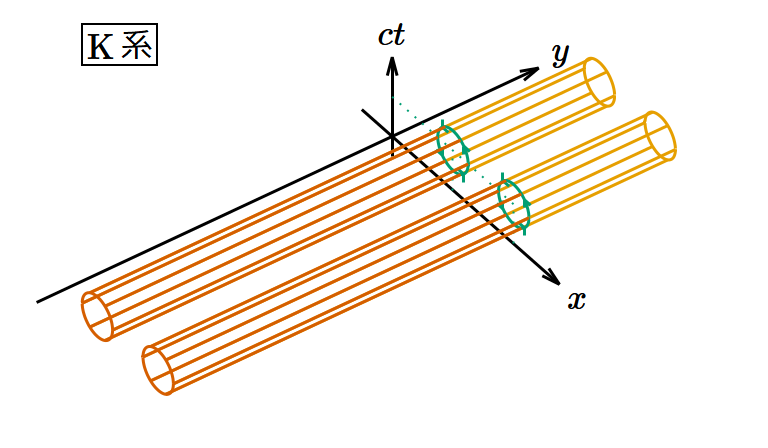
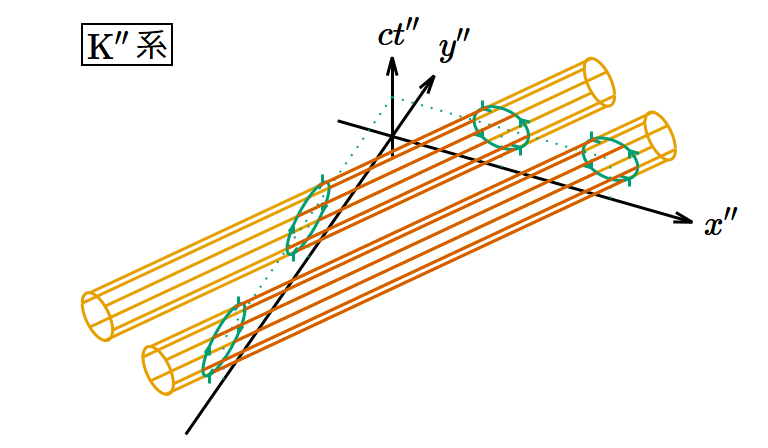
K系では渦管が 𝑥‐𝑐𝑡 平面と垂直に交差しているのに対し、K″系では渦管が 𝑥″‐𝑐𝑡″ 平面および 𝑦″‐𝑐𝑡″ 平面と斜めに交差している。 𝑥″‐𝑐𝑡″ 平面上で見た渦管の密度を考えると、 𝑥″ 方向の間隔は 𝑥 方向の間隔の 倍、 𝑐𝑡″ 方向の間隔は 𝑐𝑡 方向の間隔と同じだから、密度は 𝑥‐𝑐𝑡 平面上の密度の cos 𝜃 倍になる。同様に 𝑦″‐𝑐𝑡″ 平面上で見た渦管の密度は 𝑥‐𝑐𝑡 平面上の密度の sin 𝜃 倍になるが、よく見ると渦の向きが負になっていることがわかる。周知のように 𝐸″𝑥 = 𝐸𝑥 cos 𝜃 , 𝐸″𝑦 = −𝐸𝑥 sin 𝜃 であるから、これはちゃんとつじつまが合っている。
回転面に垂直な磁場
回転面に垂直な磁場とはすなわち 𝑧 成分のみの磁場のことである。これは図2と同じ状況である。ここで回転変換すると 𝑥‐𝑦 平面内で 𝑥 軸と 𝑦 軸が回転して 𝑥″ 軸と 𝑦″ 軸になるだけであり、 𝑥‐𝑦 平面と 𝑥″‐𝑦″ 平面は同一の平面であるから、渦の状況は変わらない(図の上で渦管の位置は変わるかもしれないが、渦管の密度や渦の向きは変わらない)。つまり 𝐵″𝑧 = 𝐵𝑧 であることを表している。
回転面に垂直な電場
回転面に垂直な電場とはすなわち 𝑧 成分のみの電場のことである。これは図3と同じ状況であり 𝑥 軸方向や 𝑦 軸方向に平行移動しても何も変わらない。したがって (𝑥, 𝑦) → (𝑥″, 𝑦″) という座標変換をしても、それらはもともとポテンシャルの渦と関係ない方向であり 𝑧 座標や 𝑐𝑡 座標には影響がないから、渦の状況は変わらない。つまり 𝐸″𝑧 = 𝐸𝑧 であることを表している。
以上のように、ポテンシャルの渦を使ったモデルで電磁場の回転変換を説明することができる。
2.3.2 ローレンツブースト変換
前節でポテンシャルを使ったモデルに慣れたところで、ここからは本題のローレンツブースト変換にこのモデルを当てはめてみる。ここでは例として、K系に対して 𝑥 軸の正方向に速度 𝑣 (> 0) で運動するK′系への変換を扱う。この場合の電場と磁場の各成分の変換を表す(8)〜(13)式を以下にもう一度書いておく。
速度に垂直な磁場
K系の電磁場のうち磁場の 𝑧 成分だけが正で他は0とする。 𝐵𝑥 = 𝐵𝑦 = 0, 𝑬 = 𝟎 を(8)〜(13)式に代入すると となる。このときK系とK′系から見たポテンシャルの渦は図6のようになる。
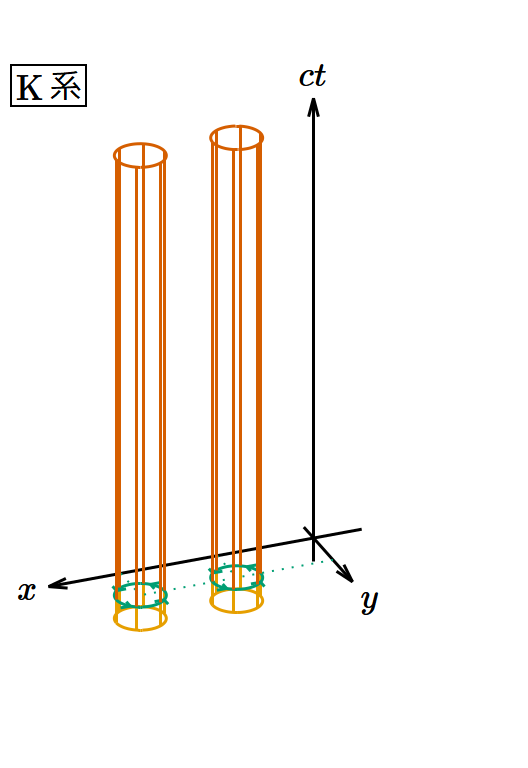
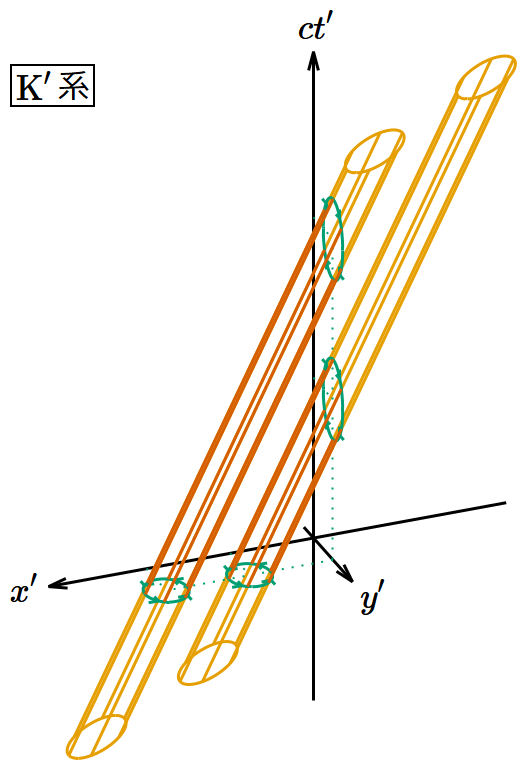
図6. 速度に垂直な磁場のローレンツブースト変換。 𝑧 軸を省略し、3つの次元のみを表示してある。 𝑧 方向に平行移動しても状況は同じである。
K系では渦管が 𝑥‐𝑦 平面と垂直に交差しているのに対し、K′系では渦管が 𝑥′‐𝑦′ 平面および 𝑦′‐𝑐𝑡′ 平面と斜めに交差している。 𝑥′‐𝑦′ 平面上では渦の向きが正なので 𝐵′𝑧 > 0 であり、 𝑦′‐𝑐𝑡′ 平面上では渦の向きが負なので 𝐸′𝑦 < 0 であることになり、符号は(18)・(19)式と整合している。
各平面と交差する渦管の密度を考えるのに図6では見にくいので、これを 𝑥‐𝑐𝑡 平面および 𝑥′‐𝑐𝑡′ 平面に投影した図7で説明しよう。なおK系において渦管の 𝑥 方向の間隔が 𝑎 だとしておく。
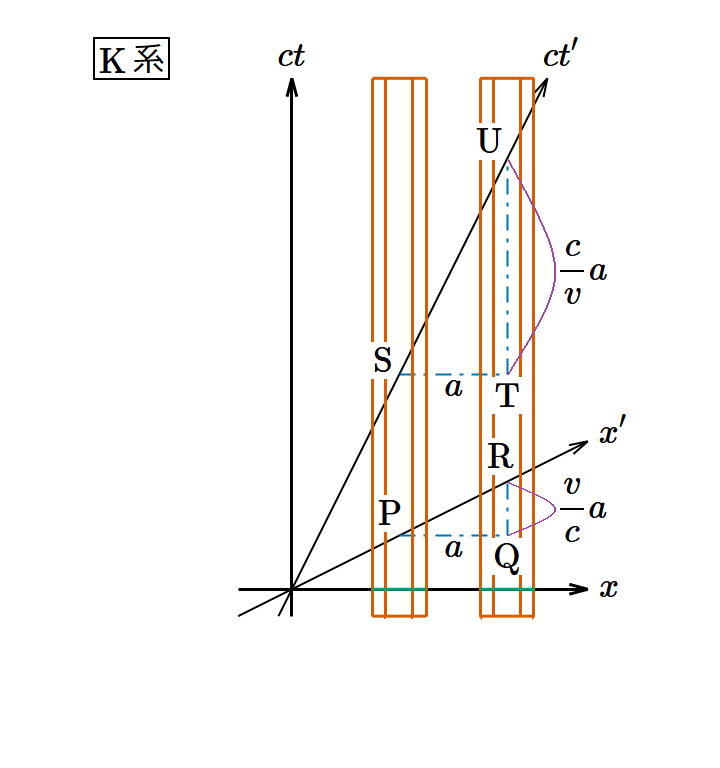
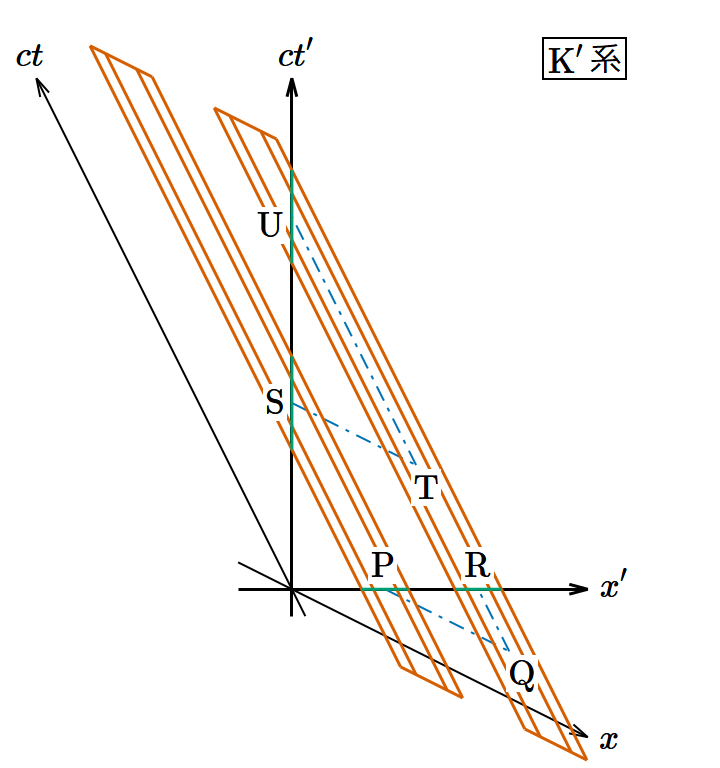
まず 𝑥′‐𝑦′ 平面と交差する渦管の密度すなわち磁場の 𝑧′ 成分の大きさについて計算する。K系でPQの距離は空間的に 𝑎 であり、 𝑥′ 軸の傾きは であるからQRの距離は時間的に になる。したがってPRの4次元的距離 𝛥𝑠 を求めると になる。これは不変量であるからK′系で測ったPRの4次元的距離 𝛥𝑠 も同じなので、K′系でPRの距離は空間的に だということになる。つまり渦管の 𝑥′ 方向の間隔は 𝑥 方向の間隔の 倍であり、 𝑦′ 方向の間隔は 𝑦 方向の間隔と同じだから、渦管の密度は 倍になる。よってこのモデルでは になり、(19)式と整合している。すでに気付いていると思うが今やった計算はまさにローレンツ収縮に他ならない。この部分に限れば磁束線を使った3次元的なモデルと理屈はだいたい同じである。
次に 𝑦′‐𝑐𝑡′ 平面と交差する渦管の密度すなわち電場の 𝑦′ 成分の大きさについて計算する。K系でSTの距離は空間的に 𝑎 であり、 𝑐𝑡′ 軸の傾きは であるからTUの距離は時間的に になる。したがってSUの4次元的距離 𝛥𝑠 を求めると になる。これは不変量であるからK′系で測ったSUの4次元的距離 𝛥𝑠 も同じなので、K′系でSUの距離は時間的に だということになる。つまり渦管の 𝑐𝑡′ 方向の時間的間隔は 𝑥 方向の空間的間隔の 倍であり、 𝑦′ 方向の間隔は 𝑦 方向の間隔と同じだから、渦管の密度は 倍になる。よってこのモデルでは になり、(18)式と整合している。左辺の絶対値の中の分母に 𝑐 がある理由は、電磁場テンソルの電場のところがそうなっているからだ。
このように、4元ポテンシャル 𝐴𝜇 の渦を用いたモデルを使えば 𝑩⟂ が 𝑬′⟂ に混じる現象も説明することができる。
速度に垂直な電場
K系の電磁場のうち電場の 𝑧 成分だけが正で他は0とする。 𝐸𝑥 = 𝐸𝑦 = 0, 𝑩 = 𝟎 を(8)〜(13)式に代入すると となる。このときK系とK′系から見たポテンシャルの渦は図8のようになる。
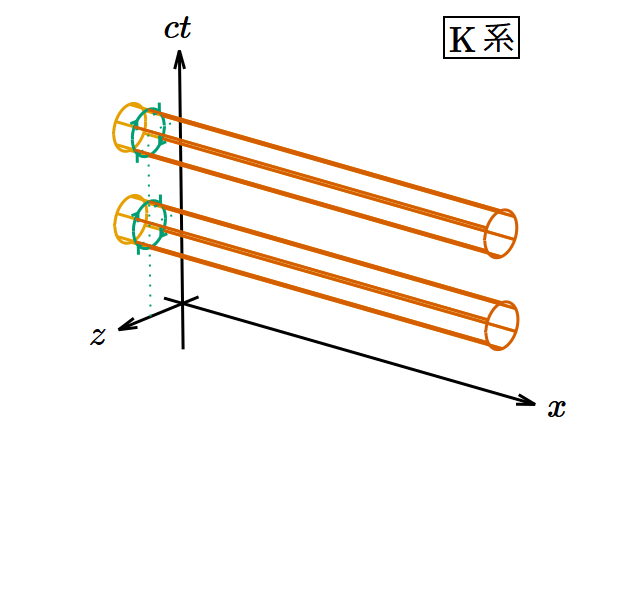
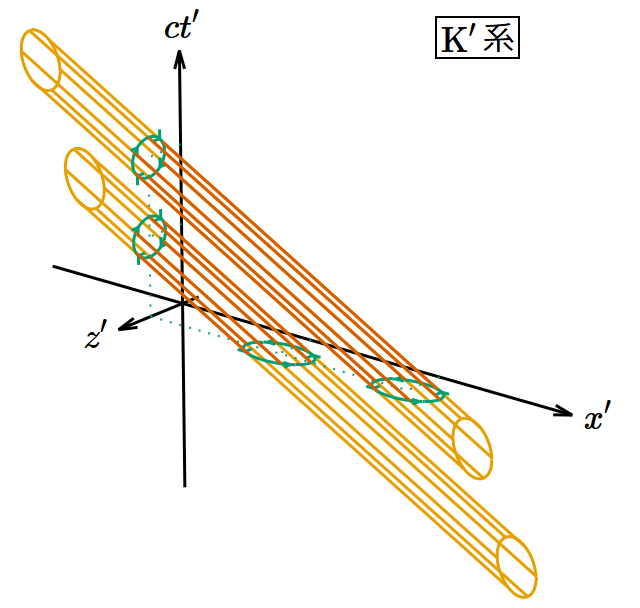
図8. 速度に垂直な電場のローレンツブースト変換。 𝑦 軸を省略し、3つの次元のみを表示してある。 𝑦 方向に平行移動しても状況は同じである。
K系では渦管が 𝑧‐𝑐𝑡 平面と垂直に交差しているのに対し、K′系では渦管が 𝑧′‐𝑐𝑡′ 平面および 𝑧′‐𝑥′ 平面と斜めに交差している。 𝑧′‐𝑐𝑡′ 平面上では渦の向きが正なので 𝐸′𝑧 > 0 であり、 𝑧′‐𝑥′ 平面上では渦の向きが正なので 𝐵′𝑦 > 0 であることになり、符号は(20)・(21)式と整合している。
各平面と交差する渦管の密度は前節の磁場のときと同様に 𝑥‐𝑐𝑡 平面および 𝑥′‐𝑐𝑡′ 平面に投影して考えればよい。よって図や途中の計算は省略し、結果だけを書くと以下のようになる。
まず 𝑧′‐𝑐𝑡′ 平面と交差する渦管の密度すなわち電場の 𝑧′ 成分の大きさに関しては、渦管の 𝑐𝑡′ 方向の間隔は 𝑐𝑡 方向の間隔の 倍であり、 𝑧′ 方向の間隔は 𝑧 方向の間隔と同じだから、渦管の密度は 倍になる。よってこのモデルでは になり、(20)式と整合している。これは動いている観測者の時間は遅れるから単位時間当たりに交差する渦管の数が増えたために電場が大きくなった、ということである。この部分は電気力線を使った3次元的なモデルではローレンツ収縮(電気力線どうしの空間的な間隔が狭くなる)で説明されたので、結果は同じだが途中の理屈が異なる。
次に 𝑧′‐𝑥′ 平面と交差する渦管の密度すなわち磁場の 𝑦′ 成分の大きさに関しては、渦管の 𝑥′ 方向の空間的間隔は 𝑐𝑡 方向の時間的間隔の 倍であり、 𝑧′ 方向の間隔は 𝑧 方向の間隔と同じだから、渦管の密度は 倍になる。よってこのモデルでは になり、(21)式と整合している。右辺の絶対値の中の分母に 𝑐 がある理由は、電磁場テンソルの電場のところがそうなっているからだ。
このように、4元ポテンシャル 𝐴𝜇 の渦を用いたモデルを使えば 𝑬⟂ が 𝑩′⟂ に混じる現象も説明することができる。
速度に平行な磁場
K系の電磁場のうち磁場の 𝑥 成分だけが正で他は0とする。 𝐵𝑦 = 𝐵𝑧 = 0, 𝑬 = 𝟎 を(8)〜(13)式に代入すると となり、何も変わらない。このときK系とK′系から見たポテンシャルの渦は図9のようになる。
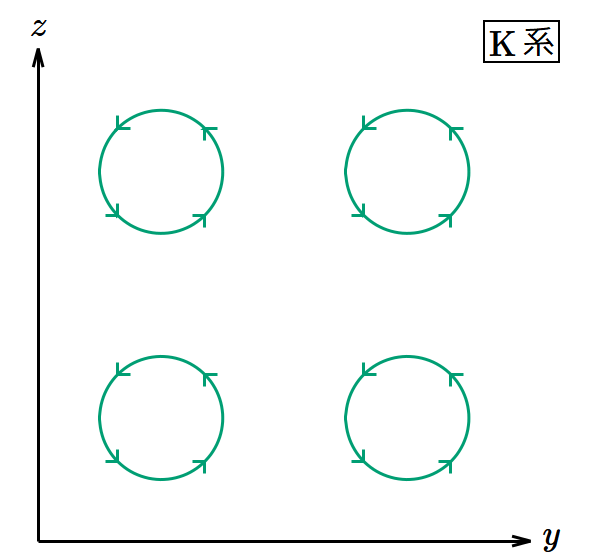
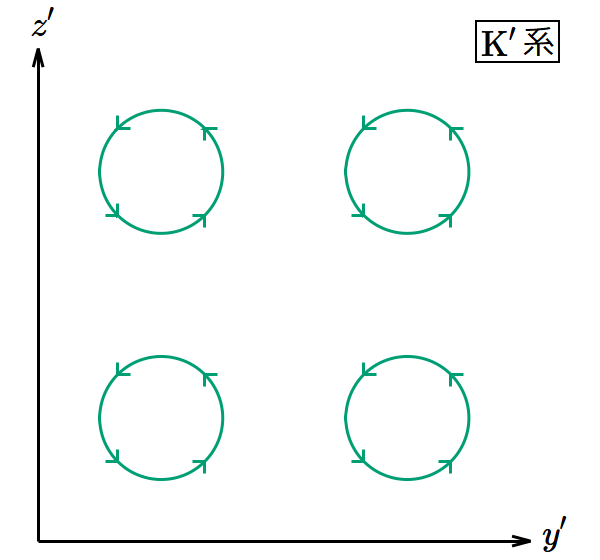
図9. 速度に平行な磁場のローレンツブースト変換。 𝑐𝑡 軸と 𝑥 軸を省略し、2つの次元のみを表示してある。 𝑐𝑡 方向および 𝑥 方向に平行移動しても状況は同じである。
ポテンシャルの渦があるのは 𝑦‐𝑧 平面で、ローレンツブースト変換により座標変換が起きるのは 𝑐𝑡 座標と 𝑥 座標であるから、両者は無関係であり、2つの図は同じである。これは磁場が何も変わらないことを表している。
速度に平行な電場
K系の電磁場のうち電場の 𝑥 成分だけが正で他は0とする。 𝐸𝑦 = 𝐸𝑧 = 0, 𝑩 = 𝟎 を(8)〜(13)式に代入すると となり、何も変わらない。このときK系とK′系から見たポテンシャルの渦は図10のようになる。
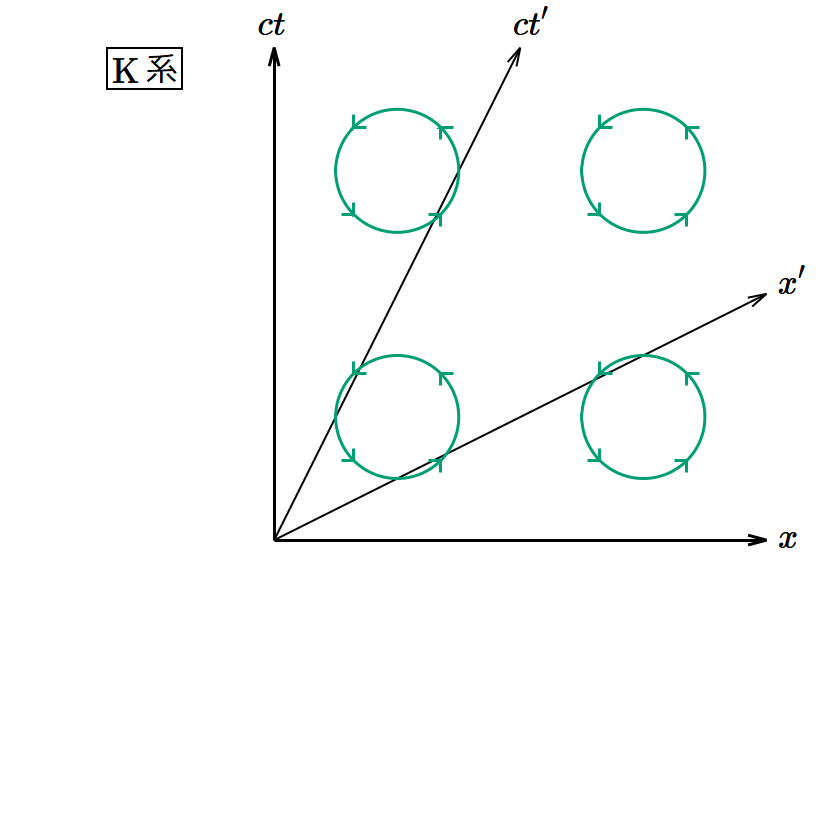
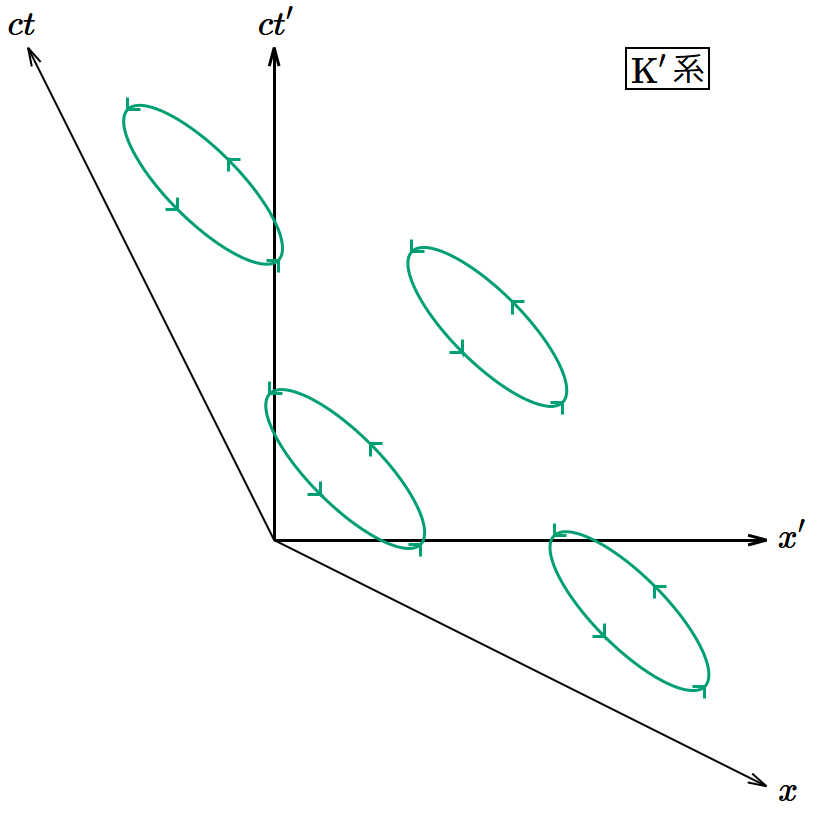
図10. 速度に平行な電場のローレンツブースト変換。 𝑦 軸と 𝑧 軸を省略し、2つの次元のみを表示してある。 𝑦 方向および 𝑧 方向に平行移動しても状況は同じである。
ポテンシャルの渦があるのは 𝑥‐𝑐𝑡 平面で、ローレンツブースト変換により座標変換が起きるのも 𝑐𝑡 座標と 𝑥 座標であるから、この2つの次元だけを考慮すればよい。K′系で渦管の密度はどうなっているのだろうか。ローレンツブースト変換では 𝑥‐𝑐𝑡 平面と 𝑥′‐𝑐𝑡′ 平面の形は変わっても面積は不変であるから、渦管の密度も1倍で変わらない。これは電場が何も変わらないことを表している。
一般の電磁場
ここまでで、速度に[垂直/平行]な[電場/磁場]という4つの成分の変換がそれぞれ4元ポテンシャル 𝐴𝜇 の渦のモデルで説明できることがわかった。その際に同時に考慮すべき次元は最大3つで済む。とても幸いなことに電磁場は重ね合わせが成り立っているから、一般の方向の電磁場のローレンツブースト変換は上に書いた4つの成分に分解して変換を考えてから最後に足し合わせればよい。
速度に垂直な成分と平行な成分に分解せずにまとめてこのモデルで扱うことはできるのだろうか。電場については成分に分けずまとめて扱ったとしても、考慮すべき次元は3つで済む。例えば速度の方向を 𝑥 軸に取り、電場の方向が 𝑥‐𝑦 平面上に来るように 𝑦 軸を取れば、 𝑥‐𝑦‐𝑐𝑡 の3次元でこのモデルを扱うことができて 𝑧 軸のことは一時的に忘れてよい。ただし定量的に正しい図を描こうとすると結局 𝑥 成分と 𝑦 成分を別々に計算する羽目になるだろう。磁場については、一般の方向の磁場をこのモデルで扱おうとするとどうしても同時に4つの次元を考慮しなければならず大変である。素直に成分に分けて考えるのが楽でよさそうだ。
最後にまとめておく。電気力線や磁束線を使った3次元的なよくあるモデルでは、なぜローレンツブースト変換で磁場の一部が電場になり電場の一部が磁場になるのかが説明できなかった。それに対し、ここで紹介した4元ポテンシャル 𝐴𝜇 の渦を使った4次元的なモデルでは電場と磁場が混じる現象も含めて電磁場のローレンツブースト変換をうまく説明することができる。電場と磁場の違いは、 𝐴𝜇 の渦が時間軸に平行か垂直かという4次元時空内での方向の違いであるから、それのローレンツブースト変換を図形的に扱う場合にも時間と空間を一体として4次元的モデルで考えるべきなのだ。