4.1 結果の一致

人工衛星の時間と地上の時間とのずれを、第一の方法（第2章）で計算した(2)式と第二の方法（第3章）で計算した(19)式は、いずれも $-\frac{3𝐺𝑀}{2{𝑐}^2𝑟}+\frac{𝐺𝑀}{{𝑐}^2𝑅}$ であった。式の見た目はまったく同じであるが、一つ注意すべきことがある。それは 𝑟 や 𝑅 の意味が2つの方法で少し異なることである。第一の方法ではこれらは普通の動径方向の距離と同じである。一方、第二の方法で使ったシュバルツシルト座標は、 𝑟 =一定の大円の長さが 2𝜋𝑟 になり 𝑟 =一定の球面の面積が 4𝜋𝑟^² になるように動径座標が振られたものであるが、空間が曲がっているために動径座標の値は動径方向の距離とは一致しない（図2）。

したがって 𝑟 は、地球中心からの距離ではなく、「軌道1周の長さが 2𝜋𝑟 である」という基準で選んだものとして考えなければならない（ 𝑅 も同様）。この基準であれば2つの方法に共通で適用できる。

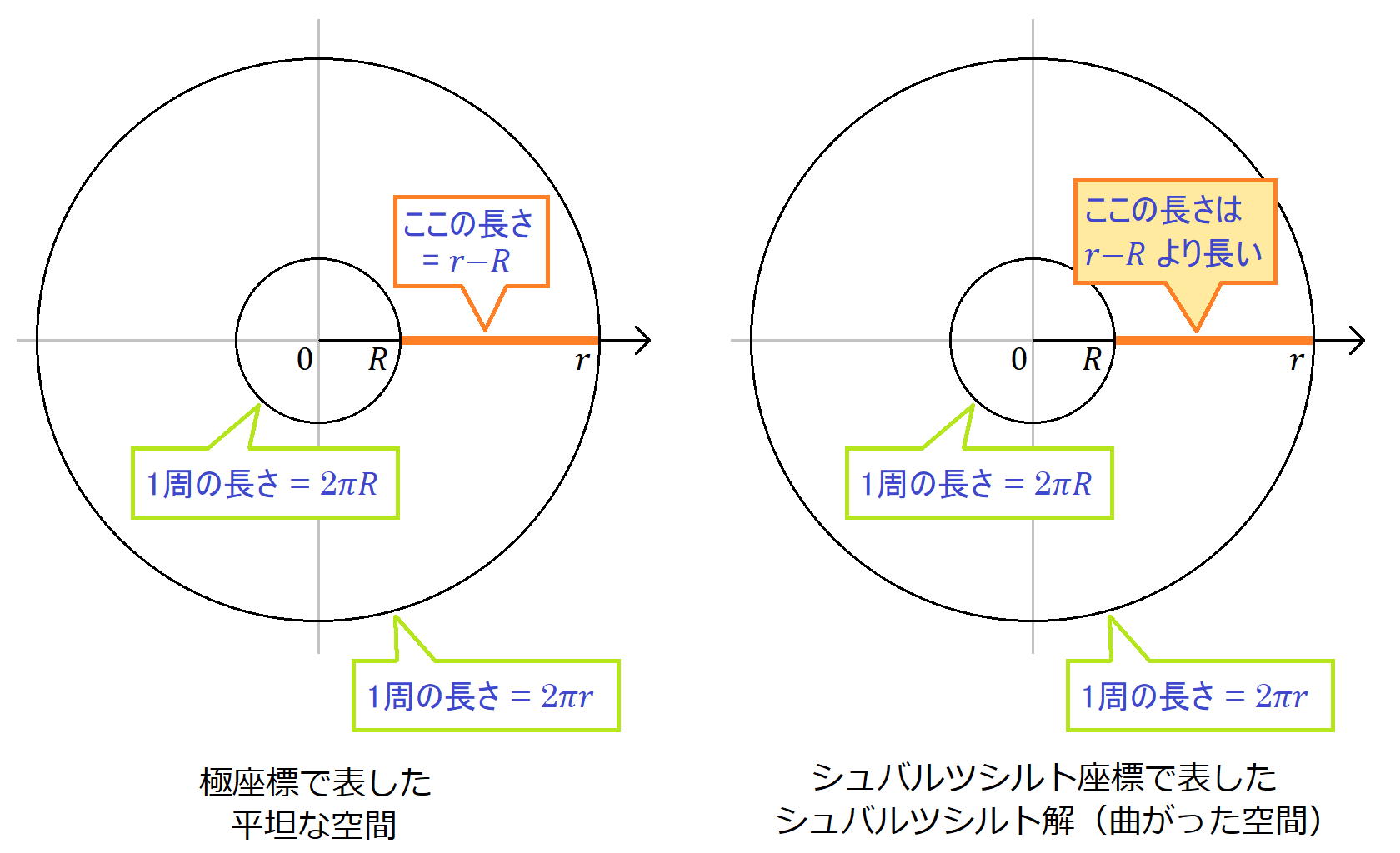
念のため空間の曲がりによって動径方向の距離がどれくらい変わるか計算してみよう。地上から軌道までの距離は、第一の方法のように空間を平坦だとみなせば 𝑟 − 𝑅 であるが、第二の方法のように空間の曲がりを考慮するとそれよりわずかに長くなる。それはどの程度の量になるのだろうか。動径方向に無限小 d𝑟 だけ離れた2点間の距離が $\sqrt{{𝑔}_{11}}\mathrm{d𝑟}=\frac{1}{\sqrt{1-\frac{{𝑟}_{𝑠}}{𝑟}}}\mathrm{d𝑟}$ であるから、これを 𝑅 から 𝑟 まで積分すればよいので、 $$\begin{array}{lll}\hfill {\int }_{𝑅}^{𝑟}\frac{1}{\sqrt{1-\frac{{𝑟}_{𝑠}}{𝑟}}}\mathrm{d𝑟}& =& {\int }_{𝑅}^{𝑟}{(1-\frac{{𝑟}_{𝑠}}{𝑟})}^{-\frac{1}{2}}\mathrm{d𝑟}\\ & \approx & {\int }_{𝑅}^{𝑟}(1+\frac{{𝑟}_{𝑠}}{2𝑟})\mathrm{d𝑟}\\ & =& [𝑟+\frac{{𝑟}_{𝑠}}{2}\ln \left|\frac{𝑟}{{𝑟}_{𝑠}}\right|{]}_{𝑅}^{𝑟}\\ & =& 𝑟-𝑅+\frac{{𝑟}_{𝑠}}{2}\ln \frac{𝑟}{𝑅}\end{array}$$ のようになる。ただし $\frac{{𝑟}_{𝑠}}{𝑟}\ll 1$ なのでこれの2次以上を無視する近似をした（近似でなく厳密に計算したければ $𝑟={𝑟}_{𝑠}{\cosh }^2𝑥$ とおいて 𝑥 で置換積分すればよい）。第3項があるおかげで 𝑟 − 𝑅 より大きくなるのだ。例えば静止軌道で第3項の値を計算すると約8㎜である。約4万㎞のうちの約8㎜であるから、全体の約50億分の1だ。

人工衛星の時間のずれを表す際に、動径座標として軌道1周の長さ÷2𝜋でなく動径方向の距離を使いたいと思う人がいるかもしれない。しかし仮にそうしたとしても、 $-\frac{3𝐺𝑀}{2{𝑐}^2𝑟}+\frac{𝐺𝑀}{{𝑐}^2𝑅}$ の中の 𝑟 や 𝑅 のところが数十億分の1倍程度変わるだけだから、気にしなくてよい（その違いは高次の微小量である）。

以上により、第一の方法と第二の方法は結果が一致したと考えることができる。

4.2 なぜ一致するのか

第一の方法（第2章）と第二の方法（第3章）は最終的に結果が一致した。途中で出てくる式は異なっているのに、最後に一致するのは不思議な感じがするかもしれない。両者のどことどこが対応しているのだろうか。

これは、地上と人工衛星の他にもう一つ、人工衛星の軌道上のどこかで静止している観測者（以下「観測者A」とする。）を考えるとわかる（図3）。観測者Aはロケット噴射するなどして地球の重力に逆らって宇宙空間に静止しているという意味である（静止軌道のことではない）。

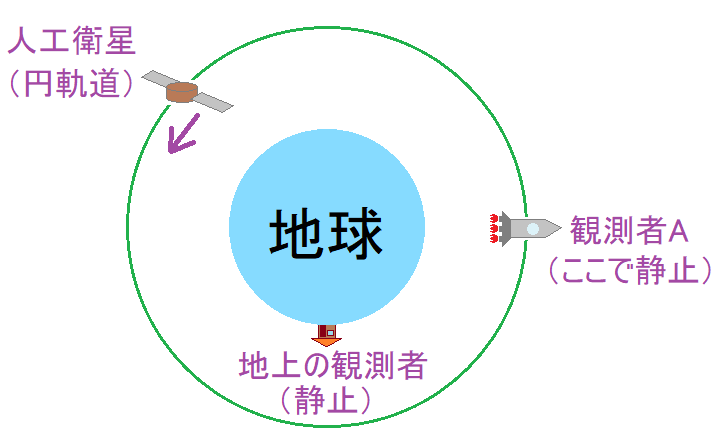
第二の方法と同様にシュバルツシルト解を使って、観測者Aの固有時を計算する。そうすると3.2節と同様の計算により観測者Aの固有時 𝜏 と座標時 𝑡 との関係は $$\begin{array}{lll}\hfill \frac{\mathrm{d𝑡}}{\mathrm{d𝜏}}& =& \frac{1}{\sqrt{1-\frac{{𝑟}_{𝑠}}{𝑟}}}\end{array}$$ となる。これを使って3.4節と同様の計算をすれば、地上と観測者Aとの時間のずれが2.3節の一般相対論的効果に一致し、観測者Aと人工衛星との時間のずれが2.2節の特殊相対論的効果に一致することがわかる。答えを知ってしまえば、どうってことのない話である。

5.1 軌道半径と時間のずれの関係

前章までで計算した結果、円軌道の人工衛星の時間 𝛥𝜏(衛) と地上の時間 𝛥𝜏(地) のずれは $$\begin{array}{lll}\hfill \frac{\mathrm{𝛥𝜏}\left(\mathrm{衛}\right)-\mathrm{𝛥𝜏}\left(\mathrm{地}\right)}{\mathrm{𝛥𝜏}\left(\mathrm{地}\right)}& =& -\frac{3𝐺𝑀}{2{𝑐}^2𝑟}+\frac{𝐺𝑀}{{𝑐}^2𝑅}\\ & =& \frac{𝐺𝑀}{{𝑐}^2}(-\frac{3}{2𝑟}+\frac{1}{𝑅})\\ & =& \frac{{𝑟}_{𝑠}}{2}(-\frac{3}{2𝑟}+\frac{1}{𝑅})\end{array}$$ であった。したがって人工衛星の時間は $𝑟<\frac{3}{2}𝑅$ なら地上より遅く進み、 $𝑟>\frac{3}{2}𝑅$ なら地上より速く進むことになる。軌道半径と時間のずれの関係を図4に示す。

オレンジ色の線が相対的な時間のずれを表す。縦の1目盛りは100億分の1であり、この量は地上で1秒が経過するごとに人工衛星と地上との間で100億分の1秒のずれが生じるという意味である。1日あたりおよび1年あたりの量は図に書き込んだとおりである。横の1目盛りは1万㎞である。人工衛星は地面より高いところを飛んでいるから軌道半径は必ず地球半径より大きくなる。図中で地球半径より小さいところは水色で塗りつぶしてある。著名な人工衛星の軌道半径を横軸に矢印で示した。

国際宇宙ステーション(ISS)では地上より遅く時間が進み、1年で0.01秒ぐらい遅れる。GPS衛星や気象衛星ひまわりでは地上より速く時間が進む。

5.2 地球の自転に伴って地上の時計が移動する場合

前節までは、地上の時間は南極点で測定することとしており、地球が自転しても地上の観測点は移動しないのであった。それでは、もし地上の時間を南極点や北極点でなく一般の場所で測定するとどうなるのだろうか。ただしここでも、地球の自転が重力場に与える影響は無視することとして、簡易的に計算する。

地球の自転の角速度を 𝜔 、観測点の緯度を 𝛼 とすれば、観測点の速度の大きさは 𝑉 = 𝜔𝑅 cos 𝛼 である。したがって地上の一般の観測点と南極点との時間の比は $$\begin{array}{lll}\hfill \sqrt{1-\frac{{𝑉}^2}{{𝑐}^2}}& =& {(1-\frac{{𝑉}^2}{{𝑐}^2})}^{\frac{1}{2}}\\ & \approx & 1-\frac{{𝑉}^2}{2{𝑐}^2}\\ & =& 1-\frac{{𝜔}^2{𝑅}^2}{2{𝑐}^2}{\cos }^2𝛼& \text{(20)}\end{array}$$ であるから時間のずれは $-\frac{{𝜔}^2{𝑅}^2}{2{𝑐}^2}{\cos }^2𝛼$ 倍である。このずれの具体的な値を計算してみよう。 $𝜔=\frac{2𝜋}{86164}\text{㎭/s}$ であるから $-\frac{{𝜔}^2{𝑅}^2}{2{𝑐}^2}$ は −1.2×10^⁻¹² である。そして cos^² 𝛼 は緯度に応じて0から1までの範囲の値を取る。このずれ（の絶対値）は赤道上で最も大きくなるが、それでも図4の縦の目盛り間隔より2桁小さい。だから今みたいな粗い話の場合、地上側の時間を地上のどこで測るかは気にしなくてよい。

(20)式の計算は2.2節（第一の方法）と同様のやり方で行ったが、4.2節と同じ理屈により、第3章（第二の方法）と同様にシュバルツシルト解を使って計算しても同じ結果になる。なおシュバルツシルト解を使う場合は座標系の角度座標を地球の緯度・経度と合わせた上で、 𝜔 は地上で測ったものであるから $\frac{\mathrm{d𝜑}}{\mathrm{d𝑡}}=\sqrt{1-\frac{{𝑟}_{𝑠}}{𝑅}}𝜔$ または $\frac{\mathrm{d𝜑}}{\mathrm{d𝜏}}=𝜔$ として計算すればよくて、 $\frac{\mathrm{d𝜑}}{\mathrm{d𝑡}}=𝜔$ とやってはいけない。

厳密なことを言えば、動いているもの同士の時間の関係はこのような単純な足し算や掛け算では計算できない。理由は4次元時空内のそれぞれの観測者の3次元同時刻面が一致しないからだ（一致するしない以前に、同時刻面を定義すること自体が難しい）。だが自転する地上と公転する人工衛星といったように周期運動している場合は、今やったような計算の結果を1周期分の平均とみなすことは構わないだろう。

最後に、地球の自転が重力場に与える影響を考慮するとどうなるのか気になるところであるが、条件設定や計算がめんどくさいし、その影響はとても小さくて計算してもあまり意味がない気がするので、ここではやらない。