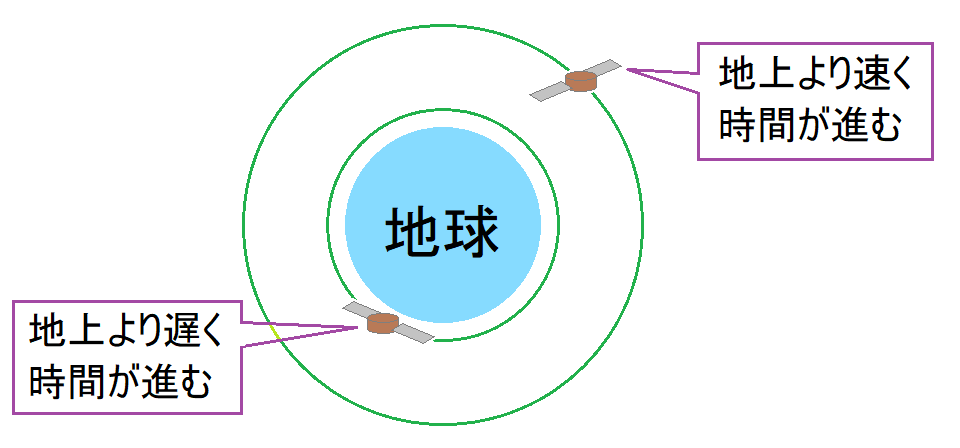
地球を周回する人工衛星の時間は、地上の時間からずれる。(図1)
そのずれを計算する方法は主に2つある。1つ目の方法は、人工衛星が動いているために生じる時間の遅れと、人工衛星が高いところに位置しているために生じる時間の進みを、別々に算出して足す方法である。2つ目の方法は、重力場の方程式の解を使ってまとめて一気に計算する方法である。
ここでは円軌道の人工衛星に対して両方のやり方で計算し、両者が同じ結果になることを示す。

地球を周回する人工衛星と、地上とでは、相対性理論で説明される時間のずれが生じる。ここでは以下のようなモデルを使って時間のずれを計算する
計算方法は次のように2つのものが考えられる。
第一の方法はこうだ。まずニュートン力学に基づいて人工衛星の軌道(高度と速度)を算出する。次に、その速度の情報を使って特殊相対性理論に基づいて人工衛星の時間の遅れ(特殊相対論的効果)を計算する。また、人工衛星の高度の情報を使って等価原理に基づいて人工衛星の時間の進み(一般相対論的効果)を計算する。これらの2つの効果による時間の遅れと進みを足し合わせれば人工衛星の時間のずれが計算できるというわけである。
第二の方法は、一般相対性理論の重力場の方程式の球対称解であるシュバルツシルト解を使って、人工衛星の固有時と地上の固有時をそれぞれ計算し、両者を比較する方法である。
世間では第一の方法のみを説明している解説が目立つ。時間がずれる原因を単純化して説明するには確かに第一の方法がやりやすい。しかし第一の方法は段階ごとにニュートン力学と特殊相対性理論と一般相対性理論を使っており、さらに3次元空間の曲がりを無視(時間軸の曲がりのみを考慮)しており、論理がわかりにくい。本当にこんな計算方法でよいのか心配になる人もいるであろう。
第二の方法は計算が少々長いがあいまいなところがなく論理が一貫していてわかりやすい。ただし話の流れを理解するためには一般相対性理論の基礎的なことがらを知っている必要があると思う。
ここでは両方の方法で計算して、それらが一致することを示す。
第一の方法とは、ニュートン力学に基づいた人工衛星の軌道に対して特殊相対論的効果と一般相対論的効果を別々に計算してそれらを足し合わせる方法である。
ニュートン力学に基づいて人工衛星の高度と速度との関係を求める。仮定により人工衛星の軌道は円軌道であるから、その運動方程式は である。ただし 𝐺 は万有引力定数、 𝑀 は地球の質量、 𝑚 は人工衛星の質量、 𝑟 は人工衛星の軌道半径、 𝑣 は人工衛星の速さである。これを変形すれば、 のようになる。𝑟 は地球中心からの距離であるから、地面からの高度よりも地球半径の分だけ大きい。
今は地球の重力があるので厳密には特殊相対性理論は成り立たないが、重力が小さいので近似的に成り立つものとする。
特殊相対性理論によれば運動する物体の時間は遅れるのであった。運動する物体の時間は静止する物体の時間の 倍になるというものである。ただし 𝑣 は物体の速さ、 𝑐 は光速である。これに(1)式を代入するのであるが、 の大きさを考えてみると仮に地面すれすれを飛ぶ人工衛星であっても約4万分の1であり1に比べてとても小さい。もっと高いところを飛ぶ人工衛星ではもっと小さい。よって、 の最低次(2次)まで計算し高次の項を無視して(1)式を代入すると である。つまり人工衛星の速度に起因する時間の進み方のずれは経過時間の 倍である。
等価原理によれば重力ポテンシャルが低い場所ほど時間は遅れるのであった。重力があまり強くないとき、重力場中の時間は基準となる場所の時間の 倍になるというものである。つまり時間の進み方のずれは経過時間の 倍である。ただし Φ(0) は基準となる場所の重力ポテンシャル、 Φ(1) は問題の場所の重力ポテンシャルである。ここで言っている「重力ポテンシャル」はニュートン力学で計算したものを使えばよい。
地球半径を 𝑅 として、 Φ(0) と Φ(1) をそれぞれ地上と軌道上の重力ポテンシャルとすれば、 である。したがって重力ポテンシャルの差に起因する時間の進み方のずれは経過時間の 倍である。 𝑅 < 𝑟 だからこれは正である。
2.2節の特殊相対論的効果による時間のずれは経過時間の 倍であり、2.3節の一般相対論的効果による時間のずれは経過時間の 倍であるから、両者を足せば人工衛星の時間のずれが算出できる。つまり、地上の経過時間を 𝛥𝜏(地) 、人工衛星の経過時間を 𝛥𝜏(衛) とすれば、 である。これが正なら人工衛星の時間が地上より早く進み、負なら人工衛星の時間が地上より遅く進む。具体的な値がどうなるかは第5章で考える。
以上が第一の方法による計算である。
第二の方法とは、一般相対性理論の重力場の方程式の球対称解を使って、人工衛星の固有時と地上の固有時をそれぞれ計算し、両者を比較する方法である。
最初に座標系を定義する。ここでは一般的なシュバルツシルト座標を使い、座標変数は以下のようにする。
ここで人工衛星の軌道が (定数)となるようにする。地球の緯度や経度とは関係なく、人工衛星の軌道を基準にして座標系を張るという意味である。球対称であるからこれは可能である。
さて、一般相対性理論では固有時 𝜏 (の微小変化)と座標変数(の微小変化)との関係は線素の式で表されるのだった。シュバルツシルト解の線素 d𝑠 の式は以下である(これの導出は「シュバルツシルト解(外部解)の導出」の記事参照)。 ただし 𝑟𝑠 はシュバルツシルト半径である。そしてこの式の全体を d𝜏² で割れば となる。 d𝑠 はもう使わないので省略した。人工衛星と地上のそれぞれについて、(3)式を使って固有時と座標変数との関係を求めていく。
地上の方が簡単なので先に済ませておこう。地上の時計は南極点で空間的に静止しているから d𝑟 = d𝜃 = d𝜑 = 0 である。また、地上における 𝑟 座標の値を 𝑟 = 𝑅 (定数)とする。これらを(3)式に代入すると、 のようになる。𝑡 は未来方向を正と定義したので最後の平方根は正のものを採用した。この式より、地上の固有時が 𝛥𝜏 だけ進んだときに座標時の変化分が になることがわかる。逆に座標時が 𝛥𝑡 だけ変化するには地上の固有時が だけ進む必要がある。
続いて人工衛星における固有時と座標変数との関係を求める。そのためには人工衛星の軌道(が満たすべき方程式)を知る必要がある。人工衛星には重力以外の力は働いていないから、その軌道(世界線)は測地線となる。それを 𝑥𝜆 とすれば、測地線方程式(運動方程式)は、 である。ただし はクリストッフェル記号、 𝜎 は媒介変数(パラメータ)である。シュバルツシルト解のクリストッフェル記号は「シュバルツシルト解のリーマン曲率テンソル」の記事の「シュバルツシルト解(外部解)のクリストッフェル記号」のところで求めてあるのでここでは結果だけを書くと、 であり、上記以外の成分は0である。また、 𝜎 はアフィンパラメータと呼ばれるものであり、それの意味の説明は省略するが、 𝑥𝜆 が時間的測地線のときは固有時 𝜏 をそのまま 𝜎 として使ってもよくて実際それが定番であるから、ここでもそうする。よって、上記のクリストッフェル記号および 𝜎 = 𝜏 を(4)式に代入すれば、測地線方程式の各成分は のようになる。
これで必要な方程式は出そろった。すなわち、地球内部を除くいたるところで成り立つべき線素の式(3)式と、測地線に対して成り立つべき測地線方程式(5)〜(8)式である。これらを使って人工衛星における固有時と座標変数との関係を求める。概念的には、まず測地線方程式から測地線の形が定まり、次に線素の式を適用することで、その測地線上をどれだけ動いたら固有時がどれだけ変化するかが定まることになる。だが結局は両方の式を使うのだから、実務上は最初からそれらの式を連立させて解けばよい。
仮定により人工衛星の軌道は円軌道であるから 𝑟 は一定なので d𝑟 = 0 である。また、 (定数)となるように座標系を張ったので d𝜃 = 0 である。そこで , を線素の式および測地線方程式に代入すると、(3)・(5)・(6)・(8)式はそれぞれ のようになり、(7)式は 0 = 0 となって消えてしまう。解くべき方程式は(9)〜(12)式である。(11)式より、 は0でないから である。(13)式を(9)式に代入し、 のようになる。𝑡 は未来方向を正と定義したので最後の平方根は正のものを採用した。また、今の問題では不要であるが(14)式を(13)式に代入すれば も求まる。𝜑 は人工衛星の進行方向を正と定義したので最後の平方根は正のものを採用した。(10)・(12)式はまだ使っていないが、今は 𝑟 が一定であるから(15)・(16)式が(10)・(12)式を満たすことはすぐにわかる。
(15)式より、人工衛星の固有時が 𝛥𝜏 だけ進んだときに座標時の変化分が になることがわかる。逆に座標時が 𝛥𝑡 だけ変化するには人工衛星の固有時が だけ進む必要がある。
[ 改稿に伴い式番号(17)は欠番になりました。 ]
座標時が 𝛥𝑡 だけ変化するとき、3.2節より地上の固有時は だけ進み、3.3節より人工衛星の固有時は だけ進む。したがって両者のずれは となる。ここで(18)式に地球のシュバルツシルト半径 を代入したいのだが、その前に や の大きさを考えてみると、 は約7億分の1であり1に比べてとても小さく、 はさらにもう少し小さい。よって、(18)式で や の最低次(1次)まで計算し高次の項を無視してから 𝑟𝑠 の表式を代入すると である。これが正なら人工衛星の時間が地上より早く進み、負なら人工衛星の時間が地上より遅く進む。具体的な値がどうなるかは第5章で考える。
以上が第二の方法による計算である。