シュバルツシルト解(外部解)のリッチテンソルはゼロであるが、リーマンテンソル(リーマン曲率テンソル)はゼロではない。ではリーマンテンソルの値はどうなっているのか、そのすべての成分を計算してみよう。
第1章 シュバルツシルト解(外部解)のクリストッフェル記号
リーマンテンソルを求めるためにはクリストッフェル記号がいるので、先にそれを求める。
最初に座標を定義する。ここで用いる座標系は一般的なシュバルツシルト座標である。座標変数は以下とする。
- 𝑥⁰ = 𝑤 (= 𝑐𝑡)
- 時間座標
- 𝑥¹ = 𝑟
- 動径座標
- 𝑥² = 𝜃
- 角度座標(緯度:北極が0)
- 𝑥³ = 𝜑
- 角度座標(経度)
ただしシュバルツシルト半径の内側では 𝑥¹ = 𝑟 は時間座標、 𝑥⁰ = 𝑤 はよくわからない空間座標である。
シュバルツシルト解の線素は
である。計量テンソル(共変テンソル)は
であり、行列で表せば対角行列となる。ここで 𝑟𝑠 はシュバルツシルト半径である。これを元にしてクリストッフェル記号を計算する
さて、重力場の方程式を解いてシュバルツシルト解(外部解)を見つけたとき、クリストッフェル記号を未知関数で表したはずだ。そのときの計算用紙が残っているなら、そこに解を代入すれば終わりである。「シュバルツシルト解(外部解)の導出」の記事の(24)式が未知関数で表したクリストッフェル記号であり、その記事の(58)・(57)式(積分定数 𝑏 = 1)が未知関数の解であるから、それを代入すれば答えが求まる。その結果、クリストッフェル記号のうち0でない成分は以下のようになる。
結果だけを知りたいならクリストッフェル記号についてはこれで完了だ。
ここからは、復習も兼ねて改めて(1)式の計量テンソルからクリストッフェル記号を求める計算を行ってみる。
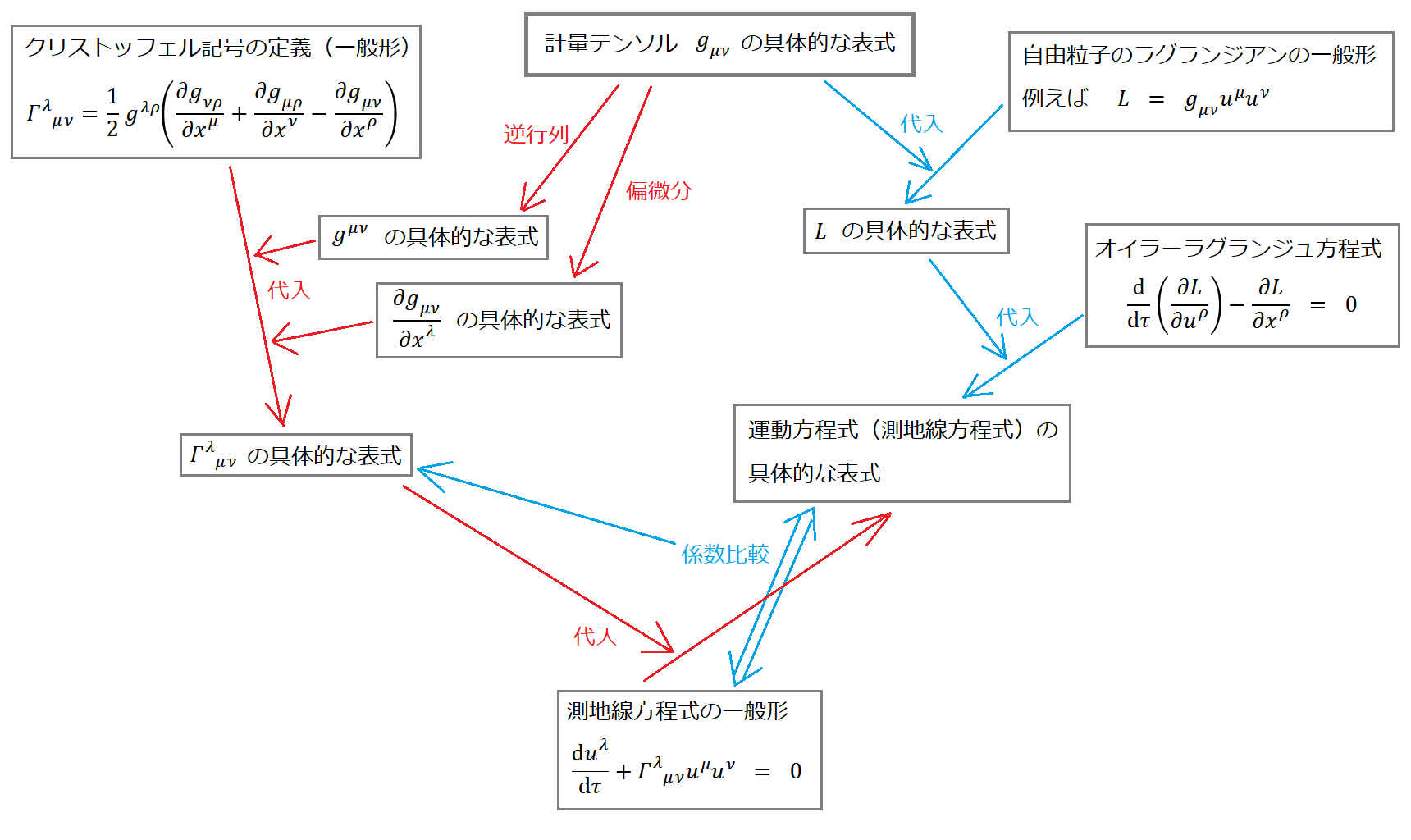
シュバルツシルト解に限らず一般的に、計量テンソルをもとにクリストッフェル記号を求める手順は大きく分けて2つある(図1)。
図1. クリストッフェル記号や測地線方程式を求める2つの手順
1つ目は図1の赤色で示したように、クリストッフェル記号の定義式に計量を代入して定義どおりに計算する方法である。2つ目は図1の青色で示したように、最小作用の原理を使って具体的な測地線方程式を求め、それを測地線方程式の一般形と比較して係数を定める方法である。以下で両方の方法で計算する。
1.1 定義にしたがってクリストッフェル記号を求める
この節では図1の赤色で示した手順でクリストッフェル記号を求める。
1.1.1 計量テンソル
クリストッフェル記号の定義は
である。見てわかるように、(2)式を計算するためには計量の反変テンソルおよび(共変テンソルの)1階微分が必要になるのでまずそれを求める。
計量の反変テンソルは共変テンソルの逆行列であるが、今は対角行列であるから対角成分を逆数にするだけでよいので
である。共変テンソルの1階微分のうち0でない成分は
である。これら以外の成分はすべて0である。
1.1.2 計量が対角行列のときに限って使える公式
慌てて(3)〜(8)式を(2)式に代入して具体的な表式を求めようとすると、計算の途中で何度も同じようなことを考えなければならず損である。計量が(1)式のような対角行列の場合は(2)式の定義式が大幅に簡略化されるのだ。この話は「シュバルツシルト解(外部解)の導出」の記事の「計量が対角行列のときに限って使えるクリストッフェル記号の公式」のところに書いたので、ここでは結果だけを書く。
計量が対角行列のときに限り、クリストッフェル記号は 𝛤 の3つの添え字のパターンに応じて次のようになる。以下①〜④の欄に限り、アインシュタインの縮約記法を使っておらず、同じ添え字が2回現れても和を取ってはならない。
① 3つの添え字がすべて等しい成分
② 上付添え字のみが異なり、2つの下付添え字が等しい成分
③ 一方の下付添え字のみが異なり、他方の下付添え字と上付添え字が等しい成分
1.1.3 クリストッフェル記号の計算
あとは1.1.1節で求めた計量テンソルとその微分を1.1.2節で導出した公式に代入するだけである。
①のパターンは、
が0でないのは(5)式の 𝜆 = 1 の場合だけであるから、
であり、これ以外の場合は0である。②のパターンは、
が0でないのは(4)・(6)〜(8)式の場合であるから、
であり、これら以外の場合は0である。③のパターンは、
が0でないのは(4)・(6)〜(8)式の場合であるから、
であり、これら以外の場合は0である。④のパターンはすべて0である。以上でクリストッフェル記号のすべての成分が求まった。
1.2 最小作用の原理からクリストッフェル記号を求める
この節では図1の青色で示した手順でクリストッフェル記号を求める。
1.2.1 ラグランジアン
相対性理論の教科書で自由粒子のラグランジアンとしてよく出てくるものは
(ただし 𝑚 は質量、 𝑐 は光速、
は四元速度、 𝜏 は固有時)である。もしも電荷・電磁場の影響がある場合は別の項が加わる。ここで −𝑚𝑐 は定数なのであまり気にしなくてよいが、ルートがついているのが面倒である。しかし電磁場の影響がない場合、ルートの中身
だけをラグランジアンとしても運動方程式が得られる。本当にそうなのか念のため確認してみよう。(9)式をオイラーラグランジュ方程式に代入すると、
両辺に をかけて縮約
となって、確かに測地線方程式(自由粒子の運動方程式)が導かれた。よってラグランジアンとして(9)式の 𝐿 を採用する。今、計量は(1)式であるから、 𝐿 の具体的な表式は
のようになる。ただしドット ˙ は固有時 𝜏 による微分 を表す。
1.2.2 オイラーラグランジュ方程式と測地線方程式の比較
今から第0〜3成分のそれぞれのオイラーラグランジュ方程式に(10)式の 𝐿 を代入する。
しかし一気に代入すると式が横長になって見にくくなるので、先に
と を別々に計算してからオイラーラグランジュ方程式に代入することにする。
第0成分(𝑤成分)
であるから、オイラーラグランジュ方程式は、
のようになる。これの波括弧内と測地線方程式の公式の第0成分
の係数を比較することにより、クリストッフェル記号は
であることがわかる。
第1成分(𝑟成分)
であるから、オイラーラグランジュ方程式は、
のようになる。これの波括弧内と測地線方程式の公式の第1成分
の係数を比較することにより、クリストッフェル記号は
であることがわかる。
第2成分(𝜃成分)
であるから、オイラーラグランジュ方程式は、
のようになる。これの波括弧内と測地線方程式の公式の第2成分
の係数を比較することにより、クリストッフェル記号は
であることがわかる。
第3成分(𝜑成分)
であるから、オイラーラグランジュ方程式は、
のようになる。これの括弧内と測地線方程式の公式の第3成分
の係数を比較することにより、クリストッフェル記号は
であることがわかる。
以上でクリストッフェル記号のすべての成分が求まった。