クリストッフェル記号

クリストッフェル記号のうち0でない成分は $$\begin{array}{lll}\hfill 𝛤^1{}_0{}_0& =& \frac{{𝑟}_{𝑠}𝑟}{4{{𝑟}_{𝑐}}^3}\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})\\ \hfill 𝛤^1{}_1{}_1& =& \frac{{𝑟}_{𝑠}𝑟}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}\\ \hfill 𝛤^1{}_2{}_2& =& -𝑟(1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3})\\ \hfill 𝛤^1{}_3{}_3& =& -𝑟(1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}){\sin }^2𝜃\\ \hfill 𝛤^2{}_3{}_3& =& -\sin 𝜃\cos 𝜃\\ \hfill 𝛤^0{}_1{}_0=𝛤^0{}_0{}_1& =& \frac{{𝑟}_{𝑠}𝑟}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})}\\ \hfill 𝛤^2{}_1{}_2=𝛤^2{}_2{}_1=𝛤^3{}_1{}_3=𝛤^3{}_3{}_1& =& \frac{1}{𝑟}\\ \hfill 𝛤^3{}_2{}_3=𝛤^3{}_3{}_2& =& \cot 𝜃\end{array}$$ である。

リーマンテンソル

リーマンテンソルの 𝑅_{𝜅𝜆𝜇𝜈} のうち0でない成分は $$\begin{array}{lll}\hfill {𝑅}_{0101}=-{𝑅}_{0110}={𝑅}_{1010}=-{𝑅}_{1001}& =& \frac{{𝑟}_{𝑠}}{4{{𝑟}_{𝑐}}^3}\cdot \frac{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\\ \hfill {𝑅}_{0202}=-{𝑅}_{0220}={𝑅}_{2020}=-{𝑅}_{2002}& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{4{{𝑟}_{𝑐}}^3}\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})\\ \hfill {𝑅}_{0303}=-{𝑅}_{0330}={𝑅}_{3030}=-{𝑅}_{3003}& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{4{{𝑟}_{𝑐}}^3}\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}){\sin }^2𝜃\\ \hfill {𝑅}_{1212}=-{𝑅}_{1221}={𝑅}_{2121}=-{𝑅}_{2112}& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}\\ \hfill {𝑅}_{1313}=-{𝑅}_{1331}={𝑅}_{3131}=-{𝑅}_{3113}& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}{\sin }^2𝜃\\ \hfill {𝑅}_{2323}=-{𝑅}_{2332}={𝑅}_{3232}=-{𝑅}_{3223}& =& \frac{{𝑟}_{𝑠}{𝑟}^4}{{{𝑟}_{𝑐}}^3}{\sin }^2𝜃\end{array}$$ であり、 𝑅^𝜅_𝜆𝜇𝜈 のうち0でない成分は $$\begin{array}{lll}\hfill 𝑅^1{}_0{}_1{}_0=-𝑅^1{}_0{}_0{}_1=𝑅^2{}_0{}_2{}_0=-𝑅^2{}_0{}_0{}_2=𝑅^3{}_0{}_3{}_0=-𝑅^3{}_0{}_0{}_3& =& \frac{{𝑟}_{𝑠}}{4{{𝑟}_{𝑐}}^3}\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})\\ \hfill 𝑅^0{}_1{}_0{}_1=-𝑅^0{}_1{}_1{}_0& =& -\frac{{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})}\\ \hfill 𝑅^2{}_1{}_2{}_1=-𝑅^2{}_1{}_1{}_2=𝑅^3{}_1{}_3{}_1=-𝑅^3{}_1{}_1{}_3& =& \frac{{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{1}{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}\\ \hfill 𝑅^0{}_2{}_0{}_2=-𝑅^0{}_2{}_2{}_0& =& -\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\\ \hfill 𝑅^1{}_2{}_1{}_2=-𝑅^1{}_2{}_2{}_1=𝑅^3{}_2{}_3{}_2=-𝑅^3{}_2{}_2{}_3& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\\ \hfill 𝑅^0{}_3{}_0{}_3=-𝑅^0{}_3{}_3{}_0& =& -\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{\sin }^2𝜃\\ \hfill 𝑅^1{}_3{}_1{}_3=-𝑅^1{}_3{}_3{}_1=𝑅^2{}_3{}_2{}_3=-𝑅^2{}_3{}_3{}_2& =& \frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}{\sin }^2𝜃\end{array}$$ である。あとあまり見かけないかもしれないが 𝑅^𝜅𝜆_𝜇𝜈 はもっと単純で、その0でない成分は $$\begin{array}{lll}\hfill 𝑅^0{}^1{}_0{}_1=-𝑅^0{}^1{}_1{}_0=𝑅^1{}^0{}_1{}_0=-𝑅^1{}^0{}_0{}_1=𝑅^0{}^2{}_0{}_2=-𝑅^0{}^2{}_2{}_0=𝑅^2{}^0{}_2{}_0=-𝑅^2{}^0{}_0{}_2=𝑅^0{}^3{}_0{}_3=-𝑅^0{}^3{}_3{}_0=𝑅^3{}^0{}_3{}_0=-𝑅^3{}^0{}_0{}_3& =& -\frac{{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\\ \hfill 𝑅^1{}^2{}_1{}_2=-𝑅^1{}^2{}_2{}_1=𝑅^2{}^1{}_2{}_1=-𝑅^2{}^1{}_1{}_2=𝑅^1{}^3{}_1{}_3=-𝑅^1{}^3{}_3{}_1=𝑅^3{}^1{}_3{}_1=-𝑅^3{}^1{}_1{}_3=𝑅^2{}^3{}_2{}_3=-𝑅^2{}^3{}_3{}_2=𝑅^3{}^2{}_3{}_2=-𝑅^3{}^2{}_2{}_3& =& \frac{{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\end{array}$$ である。

リーマンテンソルの2乗とその平方根は $$\begin{array}{lll}\hfill {𝑅}_{𝜅𝜆𝜇𝜈}{𝑅}^{𝜅𝜆𝜇𝜈}& =& \frac{12{{𝑟}_{𝑠}}^2}{{{𝑟}_{𝑐}}^6}\{\frac{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}{{(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})}^2}+1\}\\ \hfill \sqrt{{𝑅}_{𝜅𝜆𝜇𝜈}{𝑅}^{𝜅𝜆𝜇𝜈}}& =& \frac{2\sqrt{3}{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\sqrt{\frac{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}{{(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})}^2}+1}\end{array}$$ である。

リッチテンソル・スカラー曲率

内部解は外部解と違ってリッチテンソルも0ではないので、それもついでに計算しておこう。

リッチテンソル 𝑅_𝜇𝜈 はリーマンテンソルの縮約 𝑅^𝜆_𝜇𝜆𝜈 であるから、0でない成分は $$\begin{array}{l}{𝑅}_{00}=\frac{3{𝑟}_{𝑠}}{4{{𝑟}_{𝑐}}^3}\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})\\ {𝑅}_{11}=\frac{3{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{2\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{(1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3})(3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}})}\\ {𝑅}_{22}=\frac{3{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{2\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\\ {𝑅}_{33}=\frac{3{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}\cdot \frac{2\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{\sin }^2𝜃\end{array}$$ である。 𝑅^𝜇_𝜈 のうち0でない成分は $$\begin{array}{lll}\hfill 𝑅^0{}_0& =& -\frac{3{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\\ \hfill 𝑅^1{}_1=𝑅^2{}_2=𝑅^3{}_3& =& \frac{3{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{2\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}\end{array}$$ である。したがってスカラー曲率（リッチスカラー） 𝑅 は $$𝑅=\frac{6{𝑟}_{𝑠}}{{{𝑟}_{𝑐}}^3}\cdot \frac{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-2\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}{3\sqrt{1-\frac{{𝑟}_{𝑠}}{{𝑟}_{𝑐}}}-\sqrt{1-\frac{{𝑟}_{𝑠}{𝑟}^2}{{{𝑟}_{𝑐}}^3}}}$$ である。ここで計算したリッチテンソルとスカラー曲率を元の重力場の方程式（アインシュタイン方程式）に代入すると確かに成り立っていることがわかる。

スカラー量の挙動

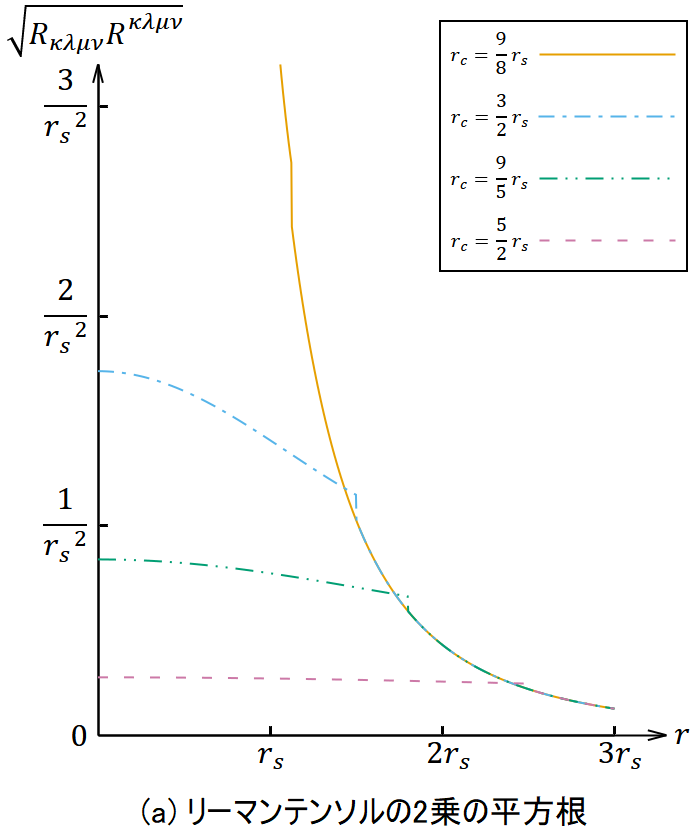
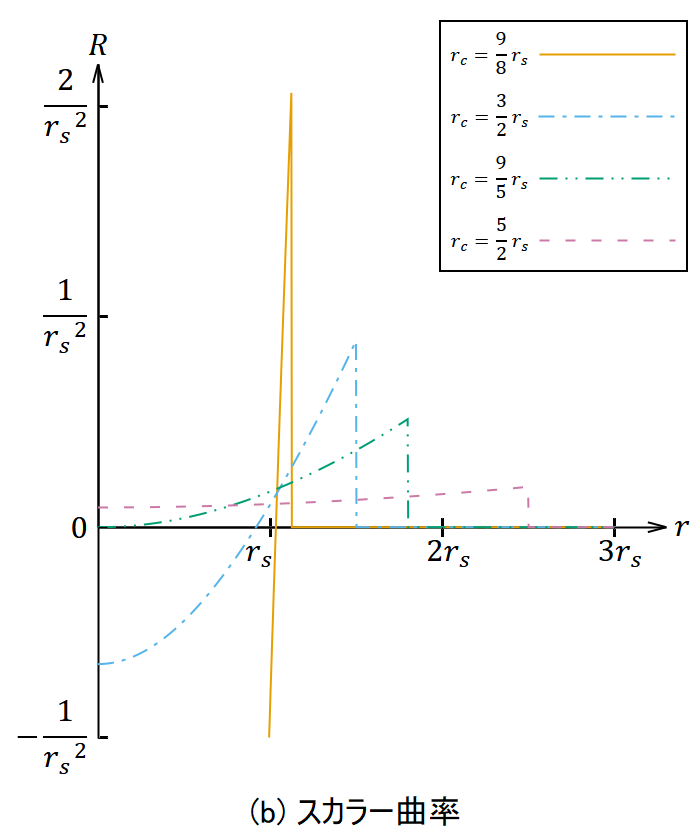
上でリーマンテンソルの2乗の平方根 $\sqrt{{𝑅}_{𝜅𝜆𝜇𝜈}{𝑅}^{𝜅𝜆𝜇𝜈}}$ とスカラー曲率 𝑅 というスカラー量が出てきた。これらが動径座標 𝑟 に対してどう変化するかを図2に示す。いずれも 𝑟 = 𝑟_𝑐 で不連続になっている。 ${𝑟}_{𝑐}=\frac{9}{8}{𝑟}_{𝑠}$ は 𝑟_𝑐 の下限であり、これ以下の 𝑟_𝑐 に対して定常状態は存在しない。 $\frac{9}{8}{𝑟}_{𝑠}<{𝑟}_{𝑐}<\frac{9}{5}{𝑟}_{𝑠}$ の場合は天体の内部で $𝑟=\frac{{𝑟}_{𝑐}}{2}\sqrt{9-\frac{5{𝑟}_{𝑐}}{{𝑟}_{𝑠}}}$ を境に 𝑅 の符号が変わるようだ。