宇宙項があったらシュバルツシルト解はどう変わるか(2)

第2章解の分類

第1章で求めた解である(22)式を(5)式に代入すると線素の式は ${d𝑠}^{2} = - (1 - \frac{1}{3} 𝛬 𝑟^{2} - \frac{𝑟_{𝑠}}{𝑟}) {d𝑤}^{2} + \frac{1}{1 - \frac{1}{3} 𝛬 𝑟^{2} - \frac{𝑟_{𝑠}}{𝑟}} {d𝑟}^{2} + 𝑟^{2} ({d𝜃}^{2} + \sin^{2} 𝜃 {d𝜑}^{2}) (23)$ である。この計量には2つの定数（宇宙定数 𝛬 とシュバルツシルト半径 𝑟_𝑠）が含まれており、それらの符号に応じて解の定性的な挙動が変わる。

2.1 （反）ドジッター解

この記事はもともと、 𝛬 が 0 でなかったらシュバルツシルト解はどう変わるのかという疑問から始まったのであり、暗黙のうちに 𝑟_𝑠 > 0 と期待していたことになる。だが先に 𝑟_𝑠 = 0 の単純な場合について考えておこう。つまり原点に何もなく真空の場合である。このときは(23)式は ${d𝑠}^{2} = - (1 - \frac{1}{3} 𝛬 𝑟^{2}) {d𝑤}^{2} + \frac{1}{1 - \frac{1}{3} 𝛬 𝑟^{2}} {d𝑟}^{2} + 𝑟^{2} ({d𝜃}^{2} + \sin^{2} 𝜃 {d𝜑}^{2}) (24)$ のようになる。もし 𝛬 = 0 ならば(24)式はただのミンコフスキー時空（に球座標を張ったもの）である。

𝛬 > 0 のとき(24)式の解を「ドジッター解」(de Sitter solution) と呼ぶ。この座標系では、原点を中心とする斥力が存在し原点から（ある程度までは）離れるほどそれが大きくるように見える。そして $𝑟 = \sqrt{\frac{3}{𝛬}}$ で 𝑔_₀₀ は0になり 𝑔_₁₁ は発散するが、うまく座標変換することでこの特異性は除去できる。そこは原点から見たら宇宙の果てのようなものであるが、その場所で時空が特殊な構造になっているわけではなく、現地にいる人から見れば他の場所と変わらない普通の時空である。 $𝑟 > \sqrt{\frac{3}{𝛬}}$ の領域では 𝑤 座標が空間的、 𝑟 座標が時間的になっている。

𝛬 < 0 のとき(24)式の解を「反ドジッター解」(Anti‐de Sitter solution) と呼ぶ。この座標系では、原点を中心とする引力が存在し原点から離れるほどそれが大きくるように見える。計量が発散してしまうような点はない。

それぞれの場合の 𝑔_₀₀ と 𝑔_₁₁ の挙動は図1のようになる。

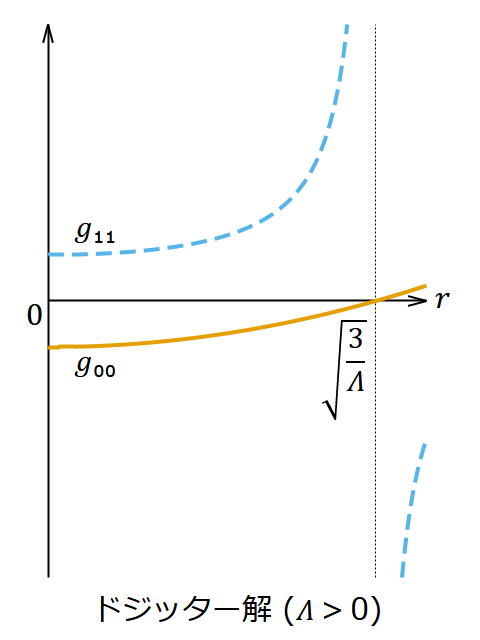
ドジッター解 (𝛬 > 0) の計量 𝑔₀₀, 𝑔₁₁ のグラフ — 図1. （反）ドジッター解の計量 𝑔_₀₀ , 𝑔_₁₁ の挙動

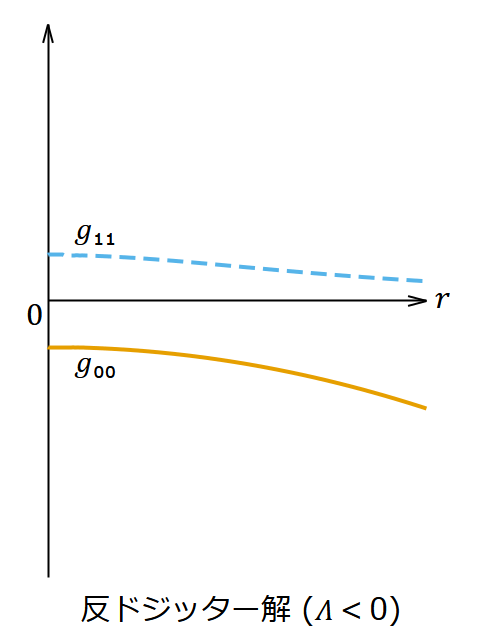
反ドジッター解 (𝛬 < 0) の計量 𝑔₀₀, 𝑔₁₁ のグラフ — 図1. （反）ドジッター解の計量 𝑔_₀₀ , 𝑔_₁₁ の挙動

ドジッター解や反ドジッター解は(24)式とは異なる別の形の計量で書かれることもよくあるが、実体は同じであり、ただ座標系の張り方が違うだけだ。どれかが間違っているというわけではない。座標変換するだけで膨張宇宙に見えたり収縮宇宙に見えたりもするのだが、その話は別の記事「ドジッター時空の座標変換と5次元への埋め込み」で説明してある。

2.2 シュバルツシルト・（反）ドジッター解

本題の 𝑟_𝑠 > 0 の場合の解 ${d𝑠}^{2} = - (1 - \frac{1}{3} 𝛬 𝑟^{2} - \frac{𝑟_{𝑠}}{𝑟}) {d𝑤}^{2} + \frac{1}{1 - \frac{1}{3} 𝛬 𝑟^{2} - \frac{𝑟_{𝑠}}{𝑟}} {d𝑟}^{2} + 𝑟^{2} ({d𝜃}^{2} + \sin^{2} 𝜃 {d𝜑}^{2}) ← (23)式$ について考えよう。 𝛬 > 0 のときは(23)式の解を「シュバルツシルト・ドジッター解」(Schwarzschild–de Sitter solution) とか「ドジッター・シュバルツシルト解」などと呼ぶ。 𝛬 < 0 のときは(23)式の解を「シュバルツシルト・反ドジッター解」(Schwarzschild–anti‐de Sitter solution) とか「反ドジッター・シュバルツシルト解」などと呼ぶ。 𝛬 = 0 ならただのシュバルツシルト解である。いずれの解も 𝑔_₀₀ = 0 になるところがあればそこに地平面ができる。

また、 𝛬 の符号にかかわらず(23)式の解を「コトラー解」(Kottler solution) とも呼ぶらしい。

シュバルツシルト・反ドジッター解

シュバルツシルト・反ドジッター解 (𝛬 < 0) の方が単純なので先にやっておく。 𝑔_₀₀ と 𝑔_₁₁ の挙動は図2のようになる。

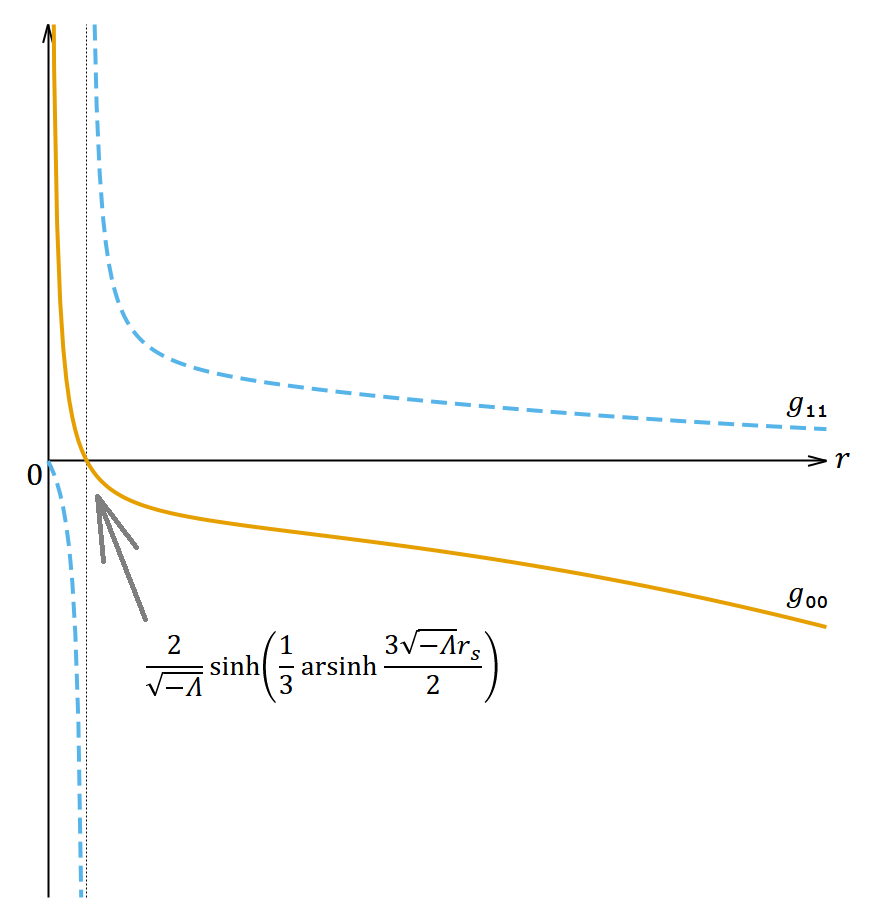
この場合、 𝛬 = 0 のときと比べてブラックホールが小さくなり、その事象の地平面の 𝑟 座標は $\begin{array}{l} 𝑟 & = & \frac{2}{\sqrt{- 𝛬}} \sinh (\frac{1}{3} arsinh \frac{3 \sqrt{- 𝛬} 𝑟_{𝑠}}{2}) \\ = & \sqrt[3]{\frac{3 𝑟_{𝑠}}{- 2 𝛬} + \frac{1}{- 𝛬} \sqrt{\frac{9 {𝑟_{𝑠}}^{2}}{4} + \frac{1}{- 𝛬}}} + \sqrt[3]{\frac{3 𝑟_{𝑠}}{- 2 𝛬} - \frac{1}{- 𝛬} \sqrt{\frac{9 {𝑟_{𝑠}}^{2}}{4} + \frac{1}{- 𝛬}}} & (25) \end{array}$ である。もし $\sqrt{- 𝛬} 𝑟_{𝑠} ≪ 1$ ならば、原点に近いところではシュバルツシルト解とほとんど同じで(25)式は近似的に $𝑟 \approx 𝑟_{𝑠} (1 + \frac{1}{3} 𝛬 {𝑟_{𝑠}}^{2})$ になり、原点から遠いところでは反ドジッター解とほとんど同じになる。

シュバルツシルト・ドジッター解

シュバルツシルト・ドジッター解 (𝛬 > 0) の 𝑔_₀₀ と 𝑔_₁₁ は $\sqrt{𝛬} 𝑟_{𝑠} = \frac{2}{3}$ を境に定性的な挙動が変わり、図3のようになる。

シュバルツシルト・ドジッター解の計量 𝑔₀₀, 𝑔₁₁ のグラフ ② √𝛬 𝑟ₛ = ⅔ のとき — 図3. シュバルツシルト・ドジッター解の計量 𝑔_₀₀ , 𝑔_₁₁ の挙動

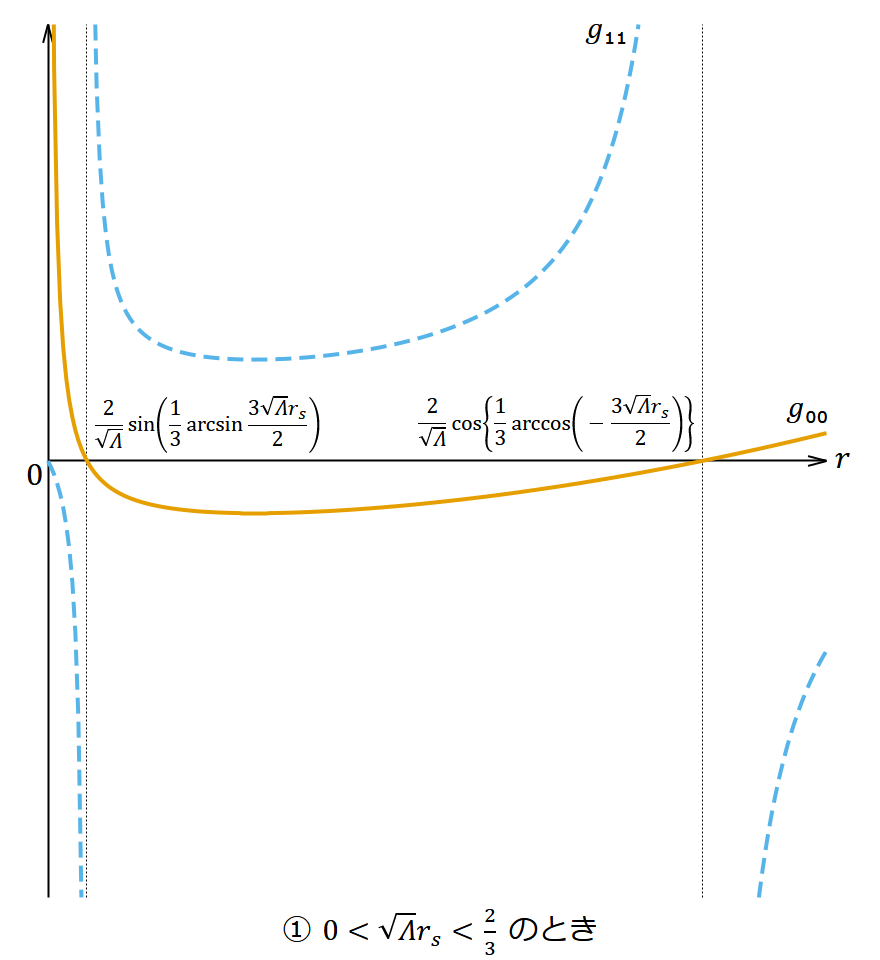
① $0 < \sqrt{𝛬} 𝑟_{𝑠} < \frac{2}{3}$ のとき: この場合、 𝛬 = 0 のときと比べてブラックホールが大きくなり、その事象の地平面の 𝑟 座標は $𝑟 = \frac{2}{\sqrt{𝛬}} \sin (\frac{1}{3} \arcsin \frac{3 \sqrt{𝛬} 𝑟_{𝑠}}{2}) (26)$ である。また、 𝑟_𝑠 = 0 のときと比べて宇宙の果てが小さくなり、その 𝑟 座標は $\begin{array}{l} 𝑟 & = & \frac{2}{\sqrt{𝛬}} \cos {\frac{1}{3} \arccos (- \frac{3 \sqrt{𝛬} 𝑟_{𝑠}}{2})} \\ = & \sqrt{\frac{3}{𝛬}} \cos (\frac{1}{3} \arcsin \frac{3 \sqrt{𝛬} 𝑟_{𝑠}}{2}) - \frac{1}{\sqrt{𝛬}} \sin (\frac{1}{3} \arcsin \frac{3 \sqrt{𝛬} 𝑟_{𝑠}}{2}) & (27) \end{array}$ である。もし $\sqrt{𝛬} 𝑟_{𝑠} ≪ 1$ ならば、原点に近いところではシュバルツシルト解とほとんど同じで(26)式は近似的に $𝑟 \approx 𝑟_{𝑠} (1 + \frac{1}{3} 𝛬 {𝑟_{𝑠}}^{2})$ になり、原点から遠いところではドジッター解ととほとんど同じで(27)式は近似的に $\begin{array}{l} 𝑟 & \approx & \sqrt{\frac{3}{𝛬}} (1 - \frac{1}{8} 𝛬 {𝑟_{𝑠}}^{2}) - \frac{1}{2} 𝑟_{𝑠} (1 + \frac{1}{3} 𝛬 {𝑟_{𝑠}}^{2}) \\ \approx & \sqrt{\frac{3}{𝛬}} - \frac{1}{2} 𝑟_{𝑠} \end{array}$ になる。
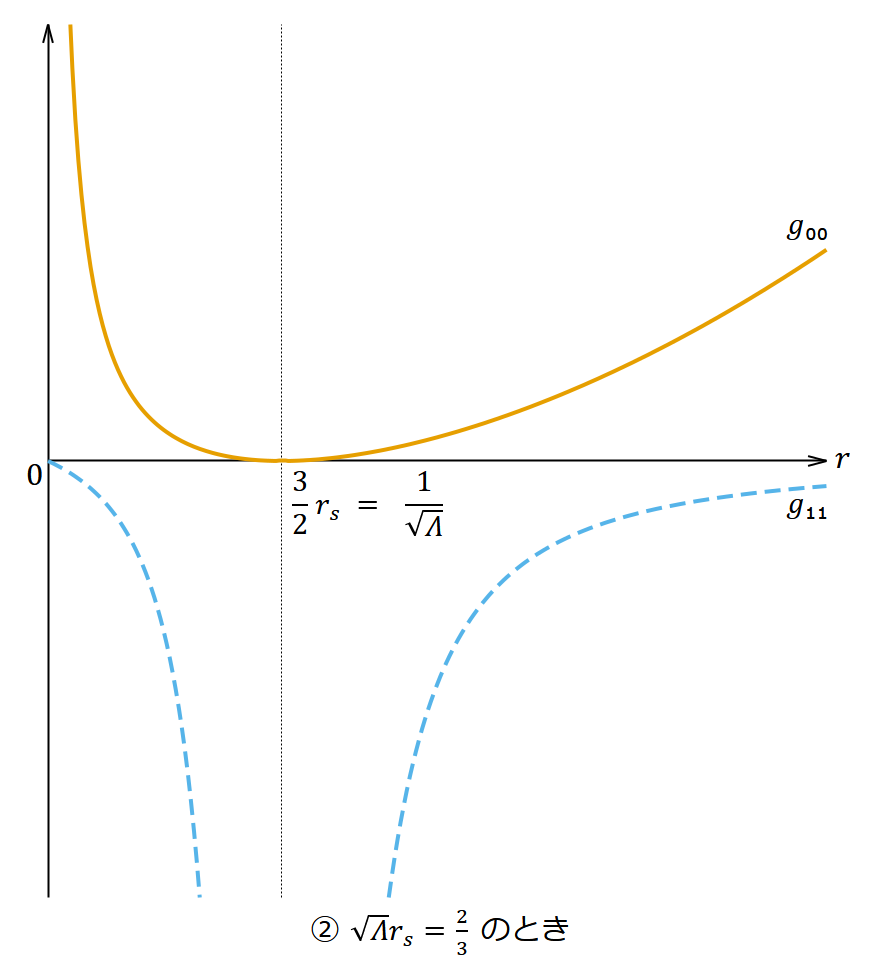
② $\sqrt{𝛬} 𝑟_{𝑠} = \frac{2}{3}$ のとき: ブラックホールの地平面が大きくなり、宇宙の果てが小さくなり、 $\begin{array}{l} 𝑟 & = & \frac{3}{2} 𝑟_{𝑠} \\ = & \frac{1}{\sqrt{𝛬}} \end{array}$ で両者の 𝑟 座標が一致する。その場所の時空の構造は一言で言えるようなものではないので説明は省略する。
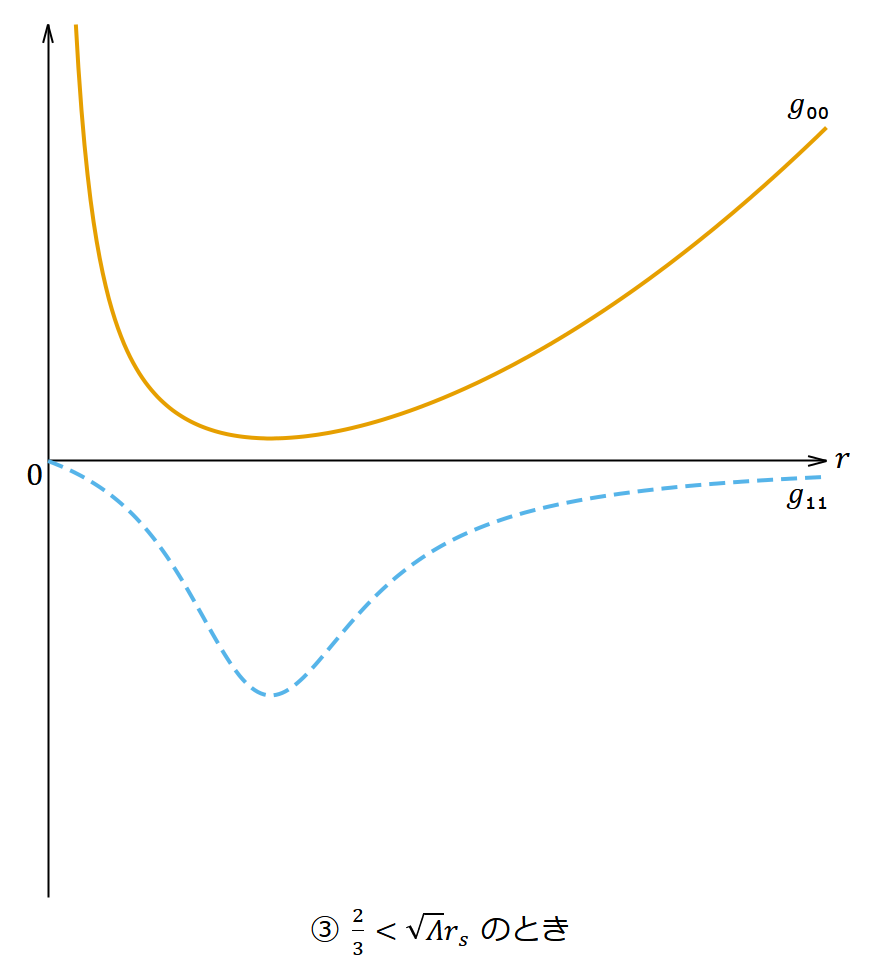
③ $\frac{2}{3} < \sqrt{𝛬} 𝑟_{𝑠}$ のとき: 𝑟 = 0 を除いて計量が発散してしまうような点はない。𝑟 > 0 の全域で 𝑤 座標が空間的、 𝑟 座標が時間的になっている。

方程式を解く前に座標系を仮定した際には、 𝑤 が時間座標で 𝑟 が動径座標だと想定していた。しかし②や③ではその想定は完全に覆されており、時空内に定常な領域は存在しなくなっている。先ほどシュバルツシルト・ドジッター解と呼ぶと言ったが、もしかしたらそれは①だけであって②や③はそう呼ばないのかもしれない。名前の定義はちょっとよくわからない。

シュバルツシルト解のときは 𝑟_𝑠 が変わっても単に全体のスケールが変わるだけあり、どれだけ大きいブラックホールがあっても特に問題はなかった。しかしシュバルツシルト・ドジッター解では上の①のように、存在できるブラックホールの質量に上限がある。それを超えると計算上は③のような変な時空になってしまう。ブラックホールでなく普通の物体の場合でも、同じように質量に上限がありそうである。しかしそれを言うためには内部解をきちんと導出してみる必要がありそうだが、面倒なのでここではやらない。