第2章 膨張・収縮しない座標系への座標変換
表1のそれぞれの解で表される時空はどのように曲がっているのだろうか。スケール因子の時間変化や空間の曲率は、式で表されているとおりである。しかしこの空間座標の目盛り間隔の実際の距離はスケール因子に比例して変わるので、宇宙全体の変化を見るのには適しているが、ある場所の近所の一定範囲内における時空の曲がり方が時間の経過とともにどう変化するかを把握するのには不便である。そこで宇宙全体の大きさの変化に影響されないような座標系を考えてみよう。(1)式を変形すると、 のようになる。ここで 𝑎𝑟 を新たな動径座標とすれば、原点を中心として表面積が一定な球面の動径座標の値を一定にすることができる。このように球面の表面積を基準とする考え方はシュバルツシルト座標の場合と同様であるが、今回は時間変化する点が異なる。このような座標系で考えれば、 𝑘 が一定ならば 𝑎 が大きくなるほど空間が平坦に近づくように思える。今からそれを実際に計算する。
2.1 宇宙定数がゼロの場合
簡単なものから先にやろう。表1で宇宙定数 𝛬 がゼロの場合の解は②と③である。
③の解は最も簡単である。 𝑎 = 1 と 𝑘 = 0 を(1)式に代入すると となって、これはただのミンコフスキー時空である。③については以上だ。
次は②の解 を考える。これは空間の曲率が負であり、複号が正なら等速膨張、負なら等速収縮である。ここで動径座標に関して という座標変換をする。 𝜌 は新しい動径座標であって、何かの密度を表しているわけではない。 𝑟 に相当するギリシャ文字をもってきただけだ。このとき逆変換は であり、その微分は のようになる。これらを2乗すれば である。(6)式を変形し(10)・(11)式を代入して座標変換後の線素の式を計算すると、 となる。これを見ると |𝑤| が大きいときほどミンコフスキー時空に近づくように見える。だが、計量の非対角成分である d𝑤d𝜌 の項があってわかりにくくなっている。これは 𝑤 軸と 𝜌 軸が直交していないということである。そこで、計量が対角になるようにさらなる座標変換を考える。動径座標はもういじりたくないので、時間座標を座標変換することで対角計量を目指そう。新しい時間座標を 𝑣 として、今のところ未知のその変換と逆変換を のように書く。 𝑣 は新しい時間座標であって、何かの速度を表しているわけではない。 𝑤 の隣のアルファベットをもってきただけだ。すると、 であるから、これらを(12)式に代入すると となる。ここで d𝑣d𝜌 の係数を0にすればよいのだが、 では困る(まともな座標変換にならない)から、 のようにすればよい。この偏微分方程式はボケっとしていると何が独立変数で何が従属変数なのか忘れそうになるので、括弧内に独立変数を明記しておいた。これを満たすような座標変換をすればよいのだが、 𝑓(𝑣) は任意と言われても手掛かりがなさ過ぎて困ってしまう。そこで、なるべく簡単になるように、特に根拠はないが試しに空間原点(𝜌 = 0)で恒等変換になるように 𝑓(𝑣) = 𝑣² としてみよう。そうすれば となる。こんなところに複号が出てきて面倒に思うかもしれないが、 𝑤 と 𝑣 の符号が同じになるように変換することと定義しておく。ところで(5)式(スケール因子)に複号がついているが、それが正のときは 𝑤 ≧ 0 、負のときは 𝑤 ≦ 0 の範囲でしか解が意味を持たないのだった。したがって(5)〜(9)式の複号と(14)・(15)式の複号は同順であると考えてよい。
(14)式より である。(14)・(16)・(17)式を(13)式に代入して座標変換後の線素の式を計算すると、 となる。これはミンコフスキー時空に球座標を張ったものであり、③の解と同じである。この計量は静的である。曲率が負の空間が等速膨張/収縮していると思っていた②の解は、単にミンコフスキー座標を座標変換しただけのものだったのだ。何かもっとややこしく曲がっている感じがしたのにとても意外な結果だ。
しかしこのことはバーコフの定理を前提にすれば当たり前である。一様・等方な空間は当然ながら任意の点に対して球対称であるから、真空ならバーコフの定理が成り立つことにより、シュバルツシルト解しかありえない。そして全空間で真空だし一様だから原点にも何も存在しないことになる。すなわち解はシュバルツシルト半径が0のシュバルツシルト解であり、それはミンコフスキー時空である、ということだ。
そういえば「バーコフの定理」の記事の最初の方で、球対称な時空の線素の式を未知関数で表すときに、うまく座標変換することで のように変形していった。先ほどやった(6)式→(12)式→(18)式の変形は(19)式→(20)式→(21)式の変形の具体例になっている。このように2段階で座標変換をすることは、その意味を理解するのには便利である。だが最初の座標系と最後の座標系が結局どういう関係になっているのかがすぐにはわからない。よって、それを求めると座標変換は である。(22)式で複号が消える理由は、(15)式の次の行で 𝑤 と 𝑣 は同符号だと定義したからである。逆変換は である。この関係を図示したものが図1・2である。茶色で描かれた座標系(静的な計量; (18)式)は時空の全体を覆うことができるが、青色で描かれた座標系(𝑘 < 0 のFLRW計量; (6)式)は、原点を頂点とする光円錐(複号が正なら未来光円錐、負なら過去光円錐)の内部だけしか言い表せないのである。 𝑤 = 0 はビッグバン/ビッグクランチかと思ったらただの座標特異点なのであった。
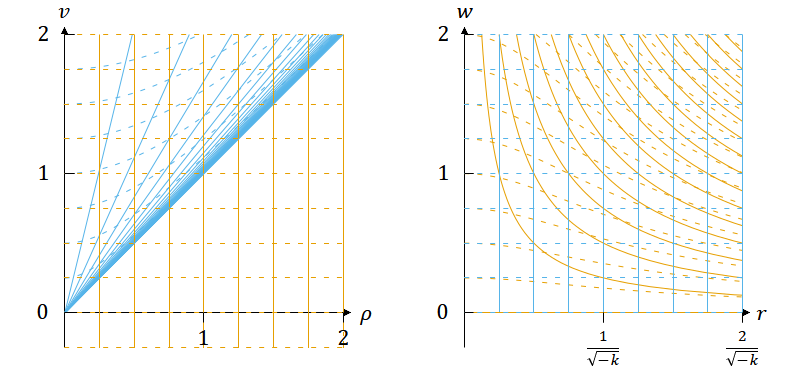
図1. スケール因子を としたFLRW計量(表1の②で複号が正)の座標変換。
茶色の線は静的な座標系、青色の線はFLRW計量の座標系を表す。後者は 𝑤 ≧ 0 の範囲で定義される。 𝑣 軸・ 𝜌 軸・ 𝑤 軸の目盛りの単位は3つの軸に共通ならmでもauでもlyでも何でもよい。
左図で青色の線が密集している 𝜌 = 𝑣 の線から右下の領域は、青色の座標系に対応する領域がない。
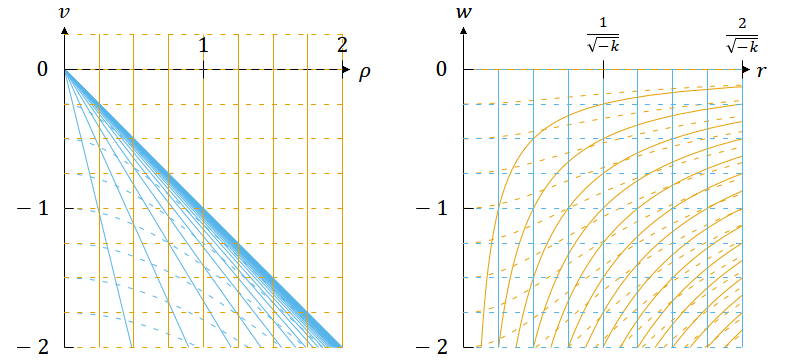
図2. スケール因子を としたFLRW計量(表1の②で複号が負)の座標変換。
茶色の線は静的な座標系、青色の線はFLRW計量の座標系を表す。後者は 𝑤 ≦ 0 の範囲で定義される。 𝑣 軸・ 𝜌 軸・ 𝑤 軸の目盛りの単位は3つの軸に共通ならmでもauでもlyでも何でもよい。
左図で青色の線が密集している 𝜌 = −𝑣 の線から右上の領域は、青色の座標系に対応する領域がない。