第3章 平坦な高次元時空への埋め込み
フリードマン方程式の真空解である表1の解は見た目は6種類(複号を区別すれば9種類)あるように見えるが、実体は宇宙定数 𝛬 の符号に応じた3種類しかなくて、座標系の張り方が違うから種類が多く見えるだけだということが第2章でわかった。それを改めて表2に示す。
| 3次元空間の曲率 𝑘 | 時空の実体 | ||||
| 𝑘 < 0 (超擬球面) |
𝑘 = 0 (平坦) |
𝑘 > 0 (超球面) |
|||
| 宇 宙 定 数 𝛬 |
𝛬 < 0 | ① | 反ドジッター時空 | ||
| 𝛬 = 0 | ② | ③ | ミンコフスキー時空 | ||
| 𝛬 > 0 | ④ | ⑤ | ⑥ | ドジッター時空 | |
| ただし | |||||
𝛬 < 0 の解はもともと①の1個だけであり、 𝛬 = 0 の解は②と③である。これらは第2章でやったような座標変換をしても3次元空間部分は開いた無限の空間になっていることに変わりはない。ところが 𝛬 > 0 の解である④〜⑥の3次元空間部分は、⑥の座標系で書けば有限の閉じた空間であるが④や⑤の座標系で書けば無限に広がる空間になっていて不思議である。ここで言っている無限に広がる空間とは、有限の距離の範囲で空間座標の値だけが∞まで変化するといった話ではなく、空間内の実際の距離が無限大まで広がっているのである。座標変換するだけでどうしてそんなことが起きるのだろうか。2.2.4節では他にもいくつか疑問が出てきたのだった。この状況を理解するには、問題の曲がった4次元時空を平坦な高次元時空(5次元ミンコフスキー時空)に埋め込んで考えると便利である。
3.1 ドジッター時空の埋め込み
2.2節でやったように、ドジッター時空の計量は次のようないろいろな表し方があった。 (130)〜(132)式はFLRW計量、(133)式は 𝜌 < 𝐿 において静的な計量である。3つのFLRW計量の座標系の座標変数はここでは同じ文字を使っているが、当然ながら別物である。FLRW計量と𝜌 < 𝐿 において静的な計量との間の座標変換は2.2節ですでに求めてあるので、後者を介すればどの座標系にも変換ができる。したがってどれか1個の座標系に関して5次元ミンコフスキー時空への埋め込み方がわかれば、あとは単純に座標変換するだけで残りの座標系の埋め込み方もわかるはずだ。
3次元超球面を4次元ユークリッド空間に埋め込む
ここでは⑥の解である(132)式をベースに考える。⑥の座標系は 𝑘 > 0 だから時間座標 𝑤 を一定にして切り取ってきた3次元断面は3次元超球面である。厳密には、この座標系では全空間の半分しかカバーできないので3次元超球面の半分であるが、同じ形の座標系を2セット持ってくれば全空間を表現できる。まず時間のことをいったん忘れてこの3次元超球面を4次元ユークリッド空間 (𝑋, 𝑌, 𝑍, 𝑈) に埋め込む。 𝑋 と 𝑌 と 𝑍 と 𝑈 は対等な4つの空間座標であり、この空間の計量は である。ここでは埋め込み先の高次元時空の座標変数を一貫して大文字で表すことにする。
今考えるべき3次元超球面の4次元空間における半径は、スケール因子を考えなければ であり、そこにスケール因子 𝑎 をかければ実際の長さは である。すなわち が3次元超球面の方程式である。このことは「一様・等方な時空の方程式とその真空解」の記事の第1章で一様・等方な3次元空間の計量の表式を考えたときのことを思い出せばたぶんわかるだろう。
ところで馬鹿正直に直交直線座標 (𝑋, 𝑌, 𝑍, 𝑈) を使い続けるとこの後の計算が無駄に面倒になって損である。どうせこの後でも(130)〜(133)式における角度座標は埋め込み先でも角度座標のまま変えないつもりなので、埋め込み先も球座標みたいな座標で表しておく。対等な4つの空間座標のうち 𝑋 と 𝑌 と 𝑍 について、普通の3次元ユークリッド空間と同様に のように座標変換すれば、(134)式の計量は となる。このような座標系 (𝑅, 𝛩, 𝛷, 𝑈) で表したところでそれが4次元ユークリッド空間であることに変わりはない。このとき3次元超球面の方程式である(135)式は となる。
この3次元超球面上で (𝑟, 𝜃, 𝜑) 座標と (𝑅, 𝛩, 𝛷, 𝑈) 座標を対応させる。角度座標はそのままにして、 𝑟 に関しては(138)式を満たすように、 のようにしてみよう。今は時間のことはいったん忘れて3次元空間部分のみを考えているから 𝑎 は定数なので、微分は である。これらを(137)式に代入すると、 となって、FLRW計量の空間部分と同じものが出てくるので、確かに(139)式の変換でよさそうである。
4次元ドジッター時空を5次元ミンコフスキー時空に埋め込む
3次元空間部分の埋め込み方は決まったので、次は時間も含めた4次元ドジッター時空を5次元ミンコフスキー時空 (𝑊, 𝑋, 𝑌, 𝑍, 𝑈) に埋め込む。 𝑊 は時間座標、 𝑋 と 𝑌 と 𝑍 と 𝑈 は対等な4つの空間座標であり、この時空の計量は である。そして先ほどと同じように、対等な4つの空間座標のうち 𝑋 と 𝑌 と 𝑍 について(136)式と同じ座標変換をして球座標みたいな座標系に変換する。すると(140)式の計量は となる。このような座標系 (𝑊, 𝑅, 𝛩, 𝛷, 𝑈) で表したところでそれが5次元ミンコフスキー時空であることに変わりはない。
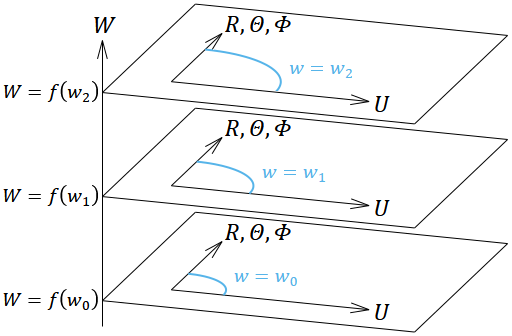
図9のように、各時刻 𝑤 における3次元超球面 (𝑟, 𝜃, 𝜑) を埋め込んだ4次元超平面 (𝑅, 𝛩, 𝛷, 𝑈) を、第5の次元である 𝑊 方向に並べてみよう。 𝑊 方向の間隔をうまく調整して、(132)式と同じ計量が実現されればよい。そこで、時間部分の変換は未定の関数 𝑓 として、空間部分は先ほどの(139)式と同じものを使いスケール因子 を代入すれば、 のようになる。今度は時間 𝑤 も変化するので、微分は である。これらを(141)式に代入すると、計量は のようになる。これと(132)式を見比べると、 d𝑟², d𝜃², d𝜑² の係数はすでに一致しており、あとは d𝑤² の係数が一致するように 𝑓 を決めればよい。したがって となる。複号や積分定数は好きなように選んで構わないので、最も簡単になるように複号は正、 𝐶 = 0 として、(142)式に代入すると、埋め込みの座標変換は のように決まる。直交直線座標で表したければ(144)〜(146)式を(136)式に代入すればよい。この4次元超曲面が満たす方程式は、ちょっと考えればわかるように、 あるいは、直交直線座標で表せば である。この式の意味は、原点からの距離が 𝐿 だということだ。つまり4次元ドジッター時空とは、5次元ミンコフスキー時空で原点から等距離にある点の集合(4次元超擬球面)と同じ形の時空であることがわかる。
この状況を図示したものが図10である。ただし5次元の絵なんてまともに描けないので、 𝑌, 𝑍 座標を省略し、 𝑌 = 𝑍 = 0 で切り取ってきた3次元断面における 𝑊, 𝑋, 𝑈 座標のみを表示している。本当は5次元ミンコフスキー時空に埋め込まれた4次元超曲面であるが、画面に見えているのは3次元ミンコフスキー時空に埋め込まれた2次元曲面であるから、残りの2つの次元は頭の中で補完してほしい。この双曲面みたいなのがドジッター時空の正体である。(149)式で表される4次元超曲面のうち、(132)式のFLRW計量の座標系の範囲外の部分は座標軸を張らずに塗りつぶしてある。
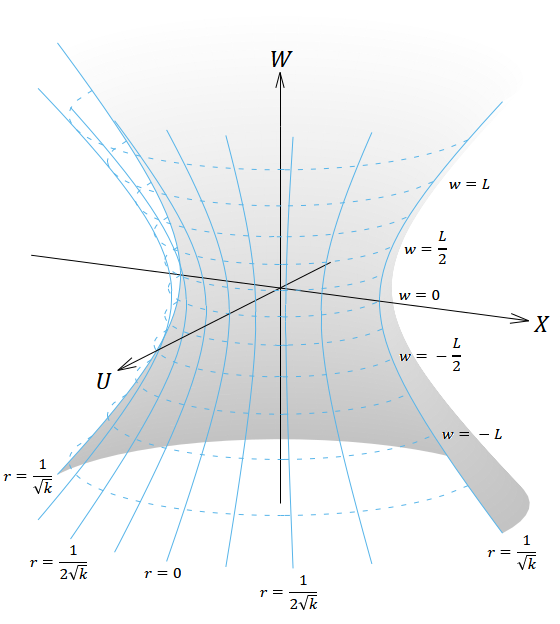
図10. 𝑘 > 0 のFLRW計量(表2の⑥)の座標系を張った4次元ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
実線は 𝑟 が一定となる線、破線は 𝑤 が一定となる線を表す。
実際は無限に広がっているがこの図は |𝑊| ≦ 2𝐿 の範囲のみを表示している。(以下この節において同じ)
時空の全体を覆うためには同じ形の座標系が2セット必要である。2セット目は(147)式の 𝑈 の符号だけを逆にして埋め込めばよい。そうすれば1セット目と2セット目の座標が滑らかにつながる。ただし空間部分の右手系と左手系が逆になる。
一見すると時刻 𝑤 = 0 で空間の大きさが最小になるように見えるかもしれないが、それは同時刻面の取り方が偏っているせいである。ドジッター時空内のすべての場所(時刻)は対等であり、特別な時刻は存在しない。普通の2次元球面と対比させて考えると、球面上のすべての点は対等であるのに緯線と経線を張ると緯度0°(赤道)が最も大きく見えてしまうことに似ている。