3.2 反ドジッター時空の埋め込み
前節ではドジッター時空を平坦な高次元時空に埋め込んだ。ドジッター時空は表2の④〜⑥のような見た目が異なる複数の座標系で表現できるが、高次元時空に埋め込むことでそれらの座標系の関係がわかりやすくなった。一方、反ドジッター時空については表2では①の解しかなくて、座標変換で移ることができる静的な座標系との関係は2.3節の図8を見ればだいたいわかる。ドジッター時空における 𝜌 = 𝐿 のようなややこしい場所もなく、座標系に切れ目が入ることもないので、もう十分だと思うかもしれない。だがそれで満足せず、ドジッター時空と同様に平坦な高次元時空に埋め込むことも考えてみよう。
2.3節でやったように、反ドジッター時空の計量は次のような複数の表し方があった。 (157)式はFLRW計量、(158)式は静的な計量である。両者の間の座標変換は2.3節ですでに求めてあるので、どちらの座標系にも変換ができる。したがってどちらか一方の座標系に関して5次元ミンコフスキー時空への埋め込み方がわかれば、あとは単純に座標変換するだけで他方の座標系の埋め込み方もわかるはずだ。
3次元超擬球面を4次元ミンコフスキー時空に埋め込む
ここでは①の解である(157)式をベースに考える。①の座標系は 𝑘 < 0 だから時間座標 𝑤 を一定にして切り取ってきた3次元断面は3次元超擬球面である。前節と同様に、まず時間のことをいったん忘れてこの3次元超擬球面を高次元空間に埋め込みたいのだが、残念ながら3次元超擬球面の全体を4次元ユークリッド空間に埋め込むことはたぶんできない(と思う)。ではどうするのかと言うと、4次元ミンコフスキー時空 (𝑉, 𝑋, 𝑌, 𝑍) に埋め込むのだ。 𝑉 は時間座標、 𝑋 と 𝑌 と 𝑍 は対等な3つの空間座標であり、この時空の計量は である。ここでは埋め込み先の高次元時空の座標変数を一貫して大文字で表すことにする。そして が3次元超擬球面の方程式である。このことは当サイトではあまり詳しく説明していないので、詳細は教科書等を見てほしい。あるいはEMAN先生の「負の曲率を持つ宇宙」がわかりやすい。
ところで馬鹿正直に直交直線座標 (𝑉, 𝑋, 𝑌, 𝑍) を使い続けるとこの後の計算が無駄に面倒になって損である。どうせこの後でも(157)・(158)式における角度座標は埋め込み先でも角度座標のまま変えないつもりなので、埋め込み先の空間部分も球座標で表しておく。空間座標 𝑋 と 𝑌 と 𝑍 について、普通の3次元ユークリッド空間と同様に のように座標変換すれば、(159)式の計量は となる。このような座標系 (𝑉, 𝑅, 𝛩, 𝛷) で表したところでそれが4次元ミンコフスキー時空であることに変わりはない。このとき3次元超擬球面の方程式である(160)式は となる。
この3次元超擬球面上で (𝑟, 𝜃, 𝜑) 座標と (𝑉, 𝑅, 𝛩, 𝛷) 座標を対応させる。角度座標はそのままにして、 𝑟 に関しては(163)式を満たすように、 のようにしてみよう。今は時間のことはいったん忘れて3次元空間部分のみを考えているから 𝑎 は定数なので、微分は である。これらを(162)式に代入すると、 となって、FLRW計量の空間部分と同じものが出てくるので、確かに(164)式の変換でよさそうである。ところで2.1節で②の解の3次元同時刻面(曲率が負の3次元空間)が4次元ミンコフスキー時空に埋め込まれていたのを覚えているだろうか。今やった埋め込みはそれと同じ状況である。
4次元反ドジッター時空を5次元ミンコフスキー時空に埋め込む
3次元空間部分の埋め込み方は決まったので、次は時間も含めた4次元反ドジッター時空を5次元ミンコフスキー時空 (𝑉, 𝑊, 𝑋, 𝑌, 𝑍) に埋め込む。 𝑉 と 𝑊 は対等な2つの時間座標、 𝑋 と 𝑌 と 𝑍 は対等な3つの空間座標であり、この時空の計量は である。「5次元ミンコフスキー時空」といえば普通は時間1次元+空間4次元が思い浮かぶが、ここでは時間2次元+空間3次元である。時間座標が2次元なんて物理的な意味を想像できないが、これは計算上の仮想的な概念だと割り切って、あまり悩まないでほしい。時間座標が2次元になっているのは埋め込み先の高次元時空だけであり、そこに埋め込まれる4次元時空の中では時間はちゃんと1次元だけになっているので心配はいらない。
先ほどと同じように、空間座標 𝑋 と 𝑌 と 𝑍 について(161)式と同じ座標変換をして球座標に変換する。すると(165)式の計量は となる。このような座標系 (𝑉, 𝑊, 𝑅, 𝛩, 𝛷) で表したところでそれが5次元ミンコフスキー時空であることに変わりはない。
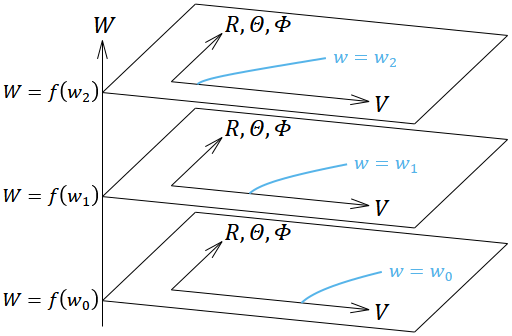
図17のように、各時刻 𝑤 における3次元超擬球面 (𝑟, 𝜃, 𝜑) を埋め込んだ4次元超平面 (𝑉, 𝑅, 𝛩, 𝛷) を、第5の次元である 𝑊 方向に並べてみよう。 𝑊 方向の間隔をうまく調整して、(157)式と同じ計量が実現されればよい。そこで、時間部分の変換は未定の関数 𝑓 として、空間部分は先ほどの(164)式と同じものを使いスケール因子 を代入すれば、 のようになる。今度は時間 𝑤 も変化するので、微分は である。これらを(166)式に代入すると、計量は のようになる。これと(157)式を見比べると、 d𝑟², d𝜃², d𝜑² の係数はすでに一致しており、あとは d𝑤² の係数が一致するように 𝑓 を決めればよい。したがって となる。複号や積分定数は好きなように選んで構わないので、最も簡単になるように複号は正、 𝐶 = 0 として、(167)式に代入すると、埋め込みの座標変換は のように決まる。直交直線座標で表したければ(170)〜(172)式を(161)式に代入すればよい。この4次元超曲面が満たす方程式は、ちょっと考えればわかるように、 あるいは、直交直線座標で表せば である。この式の意味は、原点からの距離が時間的に 𝐿 だということだ。つまり4次元反ドジッター時空とは、5次元ミンコフスキー時空(ただし時間2次元+空間3次元)で原点から時間的に等距離にある点の集合(4次元超擬球面)と同じ形の時空であることがわかる。
この状況を図示したものが図18である。ただし5次元の絵なんてまともに描けないので、 𝑌, 𝑍 座標を省略し、 𝑌 = 𝑍 = 0 で切り取ってきた3次元断面における 𝑉, 𝑊, 𝑋 座標のみを表示している。本当は5次元ミンコフスキー時空に埋め込まれた4次元超曲面であるが、画面に見えているのは3次元ミンコフスキー時空に埋め込まれた2次元曲面であるから、残りの2つの次元は頭の中で補完してほしい。この双曲面みたいなのが反ドジッター時空の正体である。(174)式で表される4次元超曲面のうち、(157)式のFLRW計量の座標系の範囲外の部分は座標軸を張らずに塗りつぶしてある。
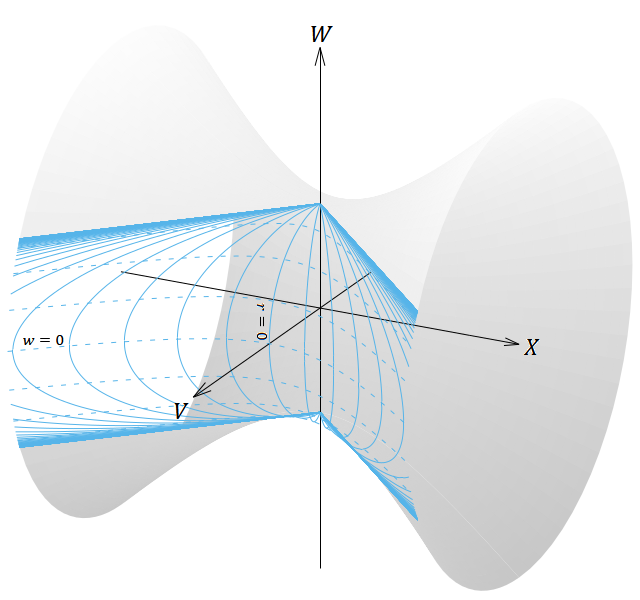
図18. 𝑘 < 0 のFLRW計量(表2の①)の座標系を張った4次元反ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
実線は 𝑟 が一定となる線、破線は 𝑤 が一定となる線を表す。 𝑤 座標の目盛り間隔は 、 𝑟 座標の目盛り間隔は である。
実際は無限に広がっているがこの図は |𝑋| ≦ 2𝐿 の範囲のみを表示している。(以下この節において同じ)
一見すると時刻 𝑤 = 0 で空間の曲がり方が最も緩やかになるように見えるかもしれないが、それは同時刻面の取り方が偏っているせいである。反ドジッター時空内のすべての場所(時刻)が対等であり、特別な時刻は存在しない。
静的な座標系の埋め込み
次に、静的な座標系 (𝑣, 𝜌) の埋め込みを求める。これと 𝑘 < 0 のFLRW計量の座標系 (𝑤, 𝑟) との座標変換は2.3節でやったとおり、 である。(127)・(128)式を(168)〜(172)式に代入すれば、 となる。(125)〜(128)式の座標変換ができるのは(157)式のFLRW計量の座標系が定義される の領域だけであるが、考えている4次元超曲面が満たすべき(173)式に(175)式を代入すると全域で成り立っているし線素の式である(166)式に(175)式を代入すると全域で(158)式と同じになるので、(175)式の埋め込みは全域で使える。この関係を図示したものが図19である。
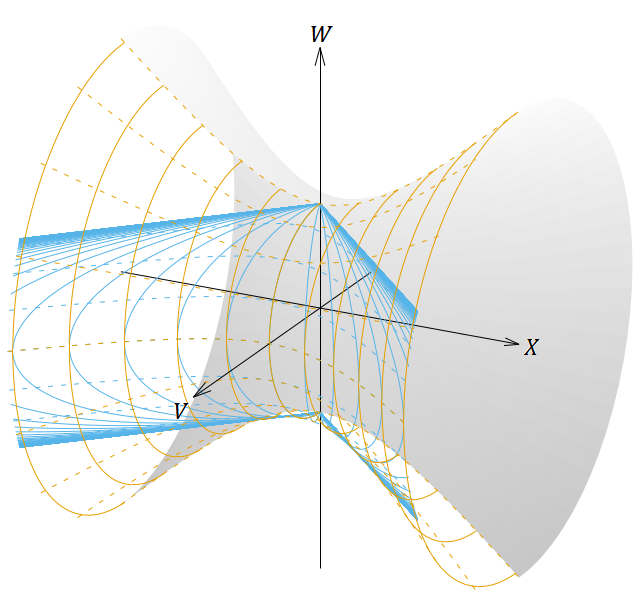
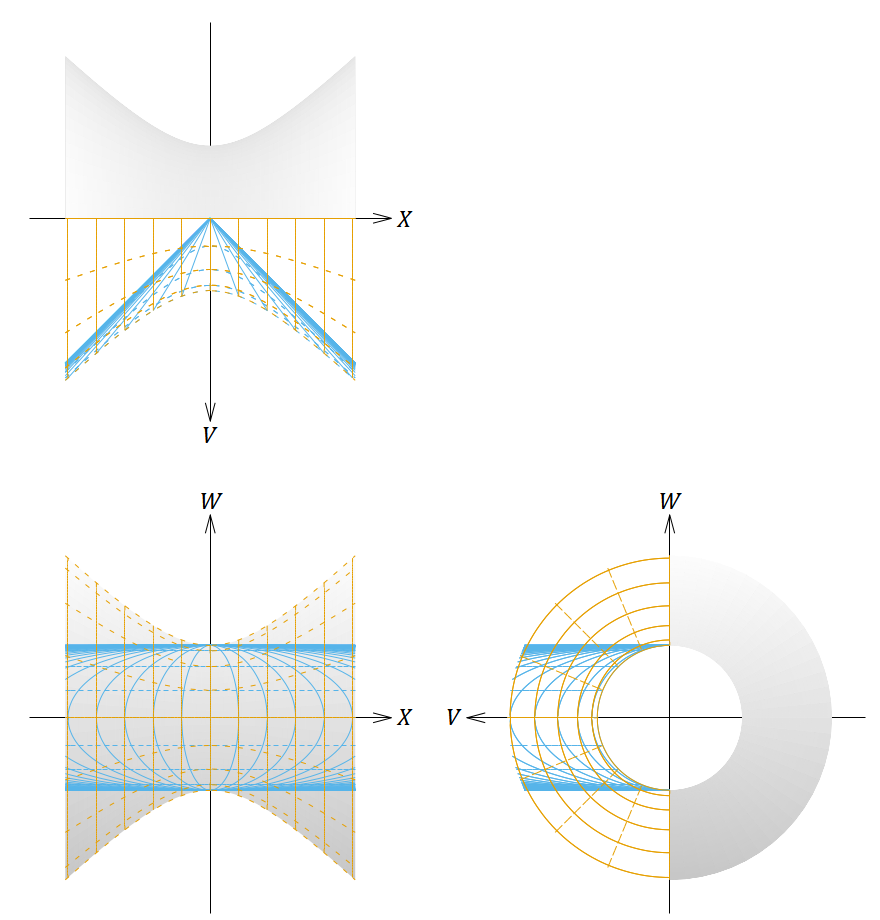
図19. 静的な座標系と 𝑘 < 0 のFLRW計量(表2の①)の座標系を張った4次元反ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
1番目の図は斜めから見た図、2〜4番目の図は正投影図である。茶色の線は静的な座標系、青色の線はFLRW計量の座標系を表す。
𝑤 が一定の青線の一部が実線のように見えるが、破線になっていると思ってほしい。
図19は曲面の全体に座標軸を張ったらごちゃごちゃして見づらくなるので、 𝑉 ≧ 0 の部分(茶色の座標系で言えば の部分)だけ座標軸を描き、 𝑉 < 0 の部分は塗りつぶしてある。これは見た目の都合でそうしただけである。前節のドジッター時空のときと違って、時空の全体を覆うために茶色の静的な座標系が2セットいるわけではなく、1セットで十分である。
これを見ると時間がループになっていて 𝑣 が 2𝜋𝐿 進んだら元の時刻に戻ってくるように見える。しかしそこはあまり気にしなくてよいだろう。4次元時空の曲がり方を人間が理解しやすいように平坦な5次元時空に埋め込んだからそうなってしまっただけである。本来リーマン幾何学はその空間内の計量だけで形を定義できて、平坦な高次元空間に埋め込む必要はないし、それができるとも限らない。また、埋め込むにしても5次元でなくもっと高次元の6次元とか7次元の時空に4次元反ドジッター時空を埋め込めば、曲率を保ったまま別の(時間的)方向に進むこともできるはずで、そうすれば未来と過去がつながらなくても済みそうだ。あるいは、仮に同じ時刻に戻ってくるとしても、この解は中身が空っぽの時空だから(古典的には)中で何も起こらないので特に矛盾はないであろう。