さまざまな座標系の埋め込み
前のページでは4次元ドジッター時空を5次元ミンコフスキー時空に埋め込むことに成功した。 𝑘 > 0 のFLRW計量の座標系 (𝑤, 𝑟, 𝜃, 𝜑) と、埋め込み先の高次元時空 (𝑊, 𝑅, 𝛩, 𝛷, 𝑈) との座標変換は、もう一度書くと である。これを手掛かりにして、残りの 𝑘 ≦ 0 のFLRW計量の座標系および 𝜌 < 𝐿 において静的な座標系についても埋め込みの座標変換式を求めよう。このページではこの先もずっと角度座標 𝛩 = 𝜃 と 𝛷 = 𝜑 は変わらないので、以下では角度座標を書くのを省略する。
最初に 𝜌 < 𝐿 において静的な座標系 (𝑣, 𝜌) の埋め込みを求める。これと 𝑘 > 0 のFLRW計量の座標系 (𝑤, 𝑟) との座標変換は2.2.3節でやったとおり、 である。(99)・(100)式を(143)〜(147)式に代入すればよい。例えば 𝐿 < 𝜌, 𝑣 < 0 の場合の 𝑈 は(99)式の3行目と(100)式の2行目を(147)式に代入すると のようになる。同様にすべての場合の 𝑊, 𝑅, 𝑈 を計算すると となる。この関係を図示したものが図11である。前のページの図10と同様に、5次元のうち 𝑊, 𝑋, 𝑈 座標の3次元のみを表示している。
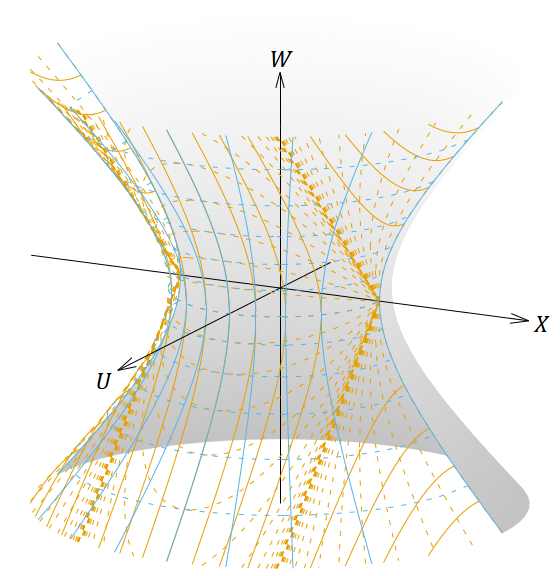
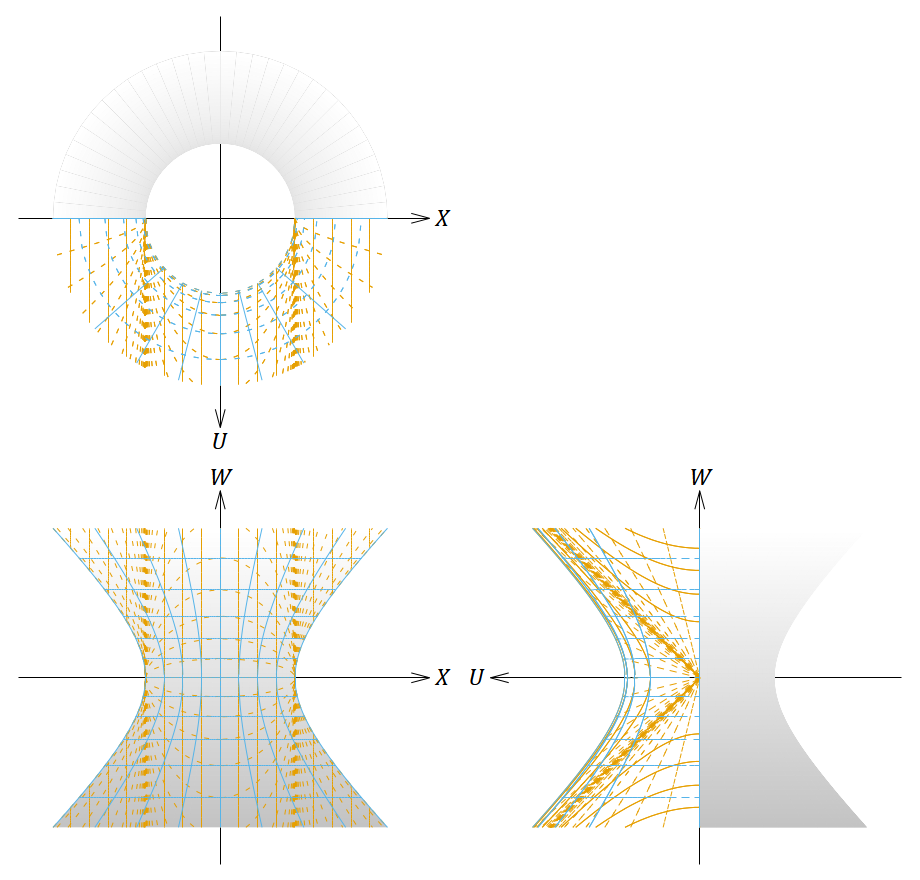
図11. 𝜌 < 𝐿 において静的な座標系と 𝑘 > 0 のFLRW計量(表2の⑥)の座標系を張った4次元ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
1番目の図は斜めから見た図、2〜4番目の図は正投影図である。茶色の線は 𝜌 < 𝐿 において静的な座標系、青色の線はFLRW計量の座標系を表す。
𝑤 が一定の青線の一部が実線のように見えるが、破線になっていると思ってほしい。
これらの2つの座標系はいずれも時空の半分 (𝑈 ≧ 0) だけを覆うので、残りの半分は座標軸を張らずに塗りつぶしてある。時空の全体を覆うためには同じ形の座標系が2セット必要である。前のページでやったように、青色の座標系の2セット目は(147)式の 𝑈 の符号だけを逆にして埋め込めばよかった。一方、茶色の座標系の2セット目で同じようにすると、 𝑈 = 0 をはさんで両側の 𝑣 座標が滑らかにつながらなくなってしまう。そこで2セット目では(150)式の 𝑊 と 𝑈 の両方の符号を逆にして埋め込めば、うまくつながるようになる。このように座標系を張ったものが図12である。
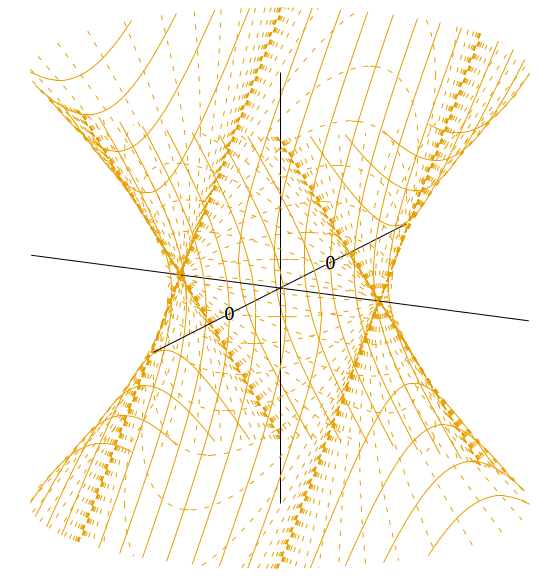
図12. 𝜌 < 𝐿 において静的な座標系(2セット)を張った4次元ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
実線は 𝜌 が一定となる線、破線は 𝑣 が一定となる線を表す。「0」と書いてあるところ(こっち側とあっち側の2か所ある)が (𝑣, 𝜌) 座標系の原点である。目盛り間隔は 𝑣 座標も 𝜌 座標も である。破線が×状に密集しているところが 𝜌 = 𝐿 、その左右が 𝜌 < 𝐿 、上下が 𝜌 > 𝐿 である。
これを 𝑊 軸の回りに回転させた画像を用意したが、サイズが大きいのでここに貼らずにリンクしておく ⇒ 回転する図12 (2294kB)。
この2セットの座標系の埋め込みをまとめて書けば、 0 ≦ 𝜌 < 𝐿 の領域に対して の2セット、 𝐿 < 𝜌 の領域に対して の2セットである。厳密には |𝑊| = |𝑈| ≠ 0 となる3次元超曲面の部分が抜けているがそこは大目に見てほしい。
次に、⑤の解である 𝑘 = 0 のFLRW計量の座標系 (𝑤, 𝑟) の埋め込みを求める。これと 𝜌 < 𝐿 において静的な座標系 (𝑣, 𝜌) との座標変換は2.2.1節でやったとおり、 である。ここで登場する複号はスケール因子 についている複号と同順である。(38)・(26)式を(151)〜(154)式に代入すればよいのだが、複号の上側に対しては(151)・(153)式を、複号の下側に対しては(151)・(154)式を使うと、 となる。言わなくてもわかると思うがこの計算では双曲線関数の定義である と を使って式変形をした。 の領域では(38)・(26)・(33)・(39)式の座標変換ができなかったが、考えている4次元超曲面が満たすべき(148)式に(155)式を代入すると全域で成り立っているし線素の式である(141)式に(155)式を代入すると全域で(131)式と同じになるので、(155)式の埋め込みは全域で使える。スケール因子の複号が正の場合について、この関係を図示したものが図13・14である。複号が負の場合は上下がひっくり返ったような図になるだけなので省略する。
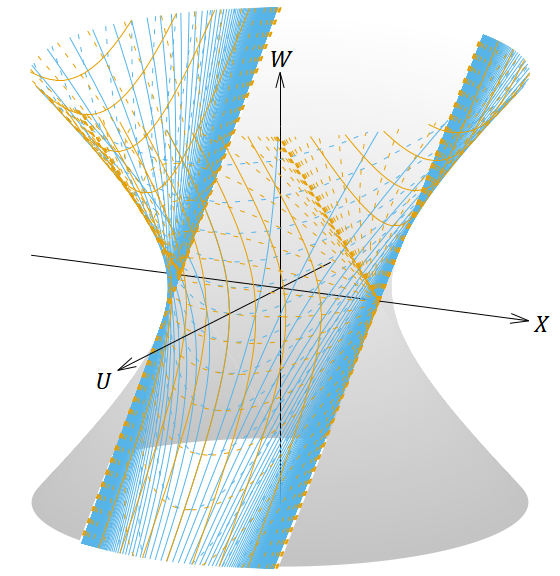
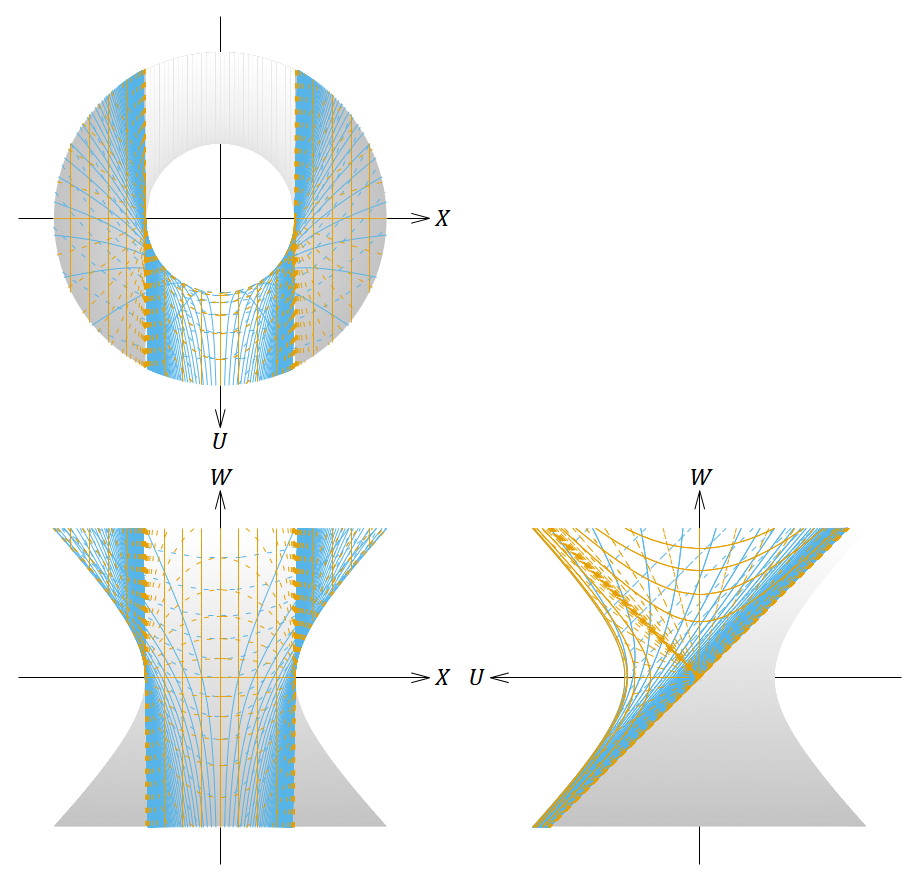
図13. 𝜌 < 𝐿 において静的な座標系と 𝑘 = 0 のFLRW計量(表2の⑤で複号が正)の座標系を張った4次元ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
1番目の図は斜めから見た図、2〜4番目の図は正投影図である。茶色の線は 𝜌 < 𝐿 において静的な座標系、青色の線はFLRW計量の座標系を表す。
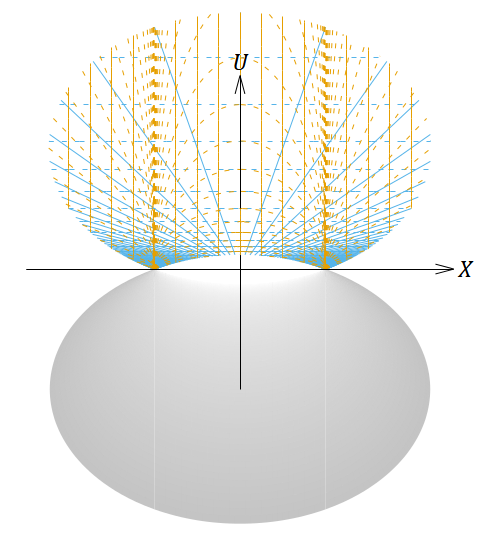
図14. 図13と同じ図形を (𝑊, 𝑋, 𝑈) = (−1, 0, 1) の斜め方向から投影した図。
𝑈 軸は上斜め手前方向を、 𝑊 軸は上斜め奥方向を向いている。線の凡例は図13と同じ。
青色の実線は図13のどの図でも直線に見えないが、図14のように (𝑊, 𝑋, 𝑈) = (−1, 0, 1) の方向から投影すれば直線に見える。
この青色の座標系も時空の半分だけを覆っている。 の座標系は 𝑊 + 𝑈 > 0 の領域、 の座標系は − 𝑊 + 𝑈 > 0 の領域である。時空の全体を覆うためには、前者の座標系をそのままに、後者の座標系の 𝑈 座標の符号を逆にして埋め込めばよい。その図を描くのはもう面倒なので省略する。平坦な空間が永久に指数関数的に膨張する時空と収縮する時空を合わせたものが、ドジッター時空の全体になるのだ。厳密には 𝑊 + 𝑈 = 0 となる3次元超曲面の部分(2つの座標系の境界面)が抜けているがそこは大目に見てほしい。
このように、⑥の解である(132)式のFLRW計量 (𝑘 > 0) と⑤の解である(131)式のFLRW計量 (𝑘 = 0) はともにドジッター時空の半分を覆うが、半分に分ける分け方が異なる。図11は縦に切っているが図13は斜めに切っている。2.2.4節で出てきた疑問の一つに、図7の左図の座標系には切れ目があるが図3・4の左図の座標系にはそのようなものがないのはなぜか、矛盾ではないのか、というものがあった。その答えがこれである。つまりドジッター時空の全体を半分に切る分け方によって切れ目があったりなかったりするのだ。
最後に、④の解である 𝑘 < 0 のFLRW計量の座標系 (𝑤, 𝑟) の埋め込みを求める。これと 𝜌 < 𝐿 において静的な座標系 (𝑣, 𝜌) との座標変換は2.2.2節でやったとおり、 である。ここで登場する複号はスケール因子 についている複号と同順であるとともに、 𝑤 や 𝑣 と同符号でもある。(67)・(68)式を(150)式または(151)〜(154)式に代入すれば、 となる。複号の上側に対しては(151)・(153)式を、複号の下側に対しては(151)・(154)式を使ったと考えてもよいし、(150)式だけを使ったと考えてもよい。 の領域では(67)〜(70)式の座標変換ができなかったが、考えている4次元超曲面が満たすべき(148)式に(156)式を代入すると全域で成り立っているし線素の式である(141)式に(156)式を代入すると全域で(130)式と同じになるので、(156)式の埋め込みは全域で使える。スケール因子の複号が正の場合について、この関係を図示したものが図15である。複号が負の場合は上下がひっくり返ったような図になるだけなので省略する。
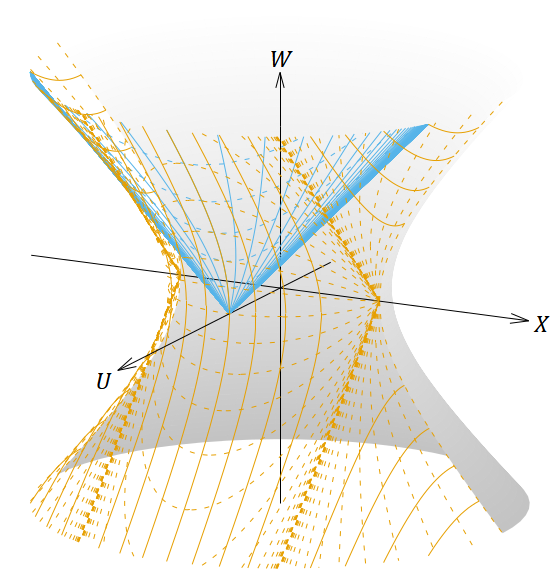
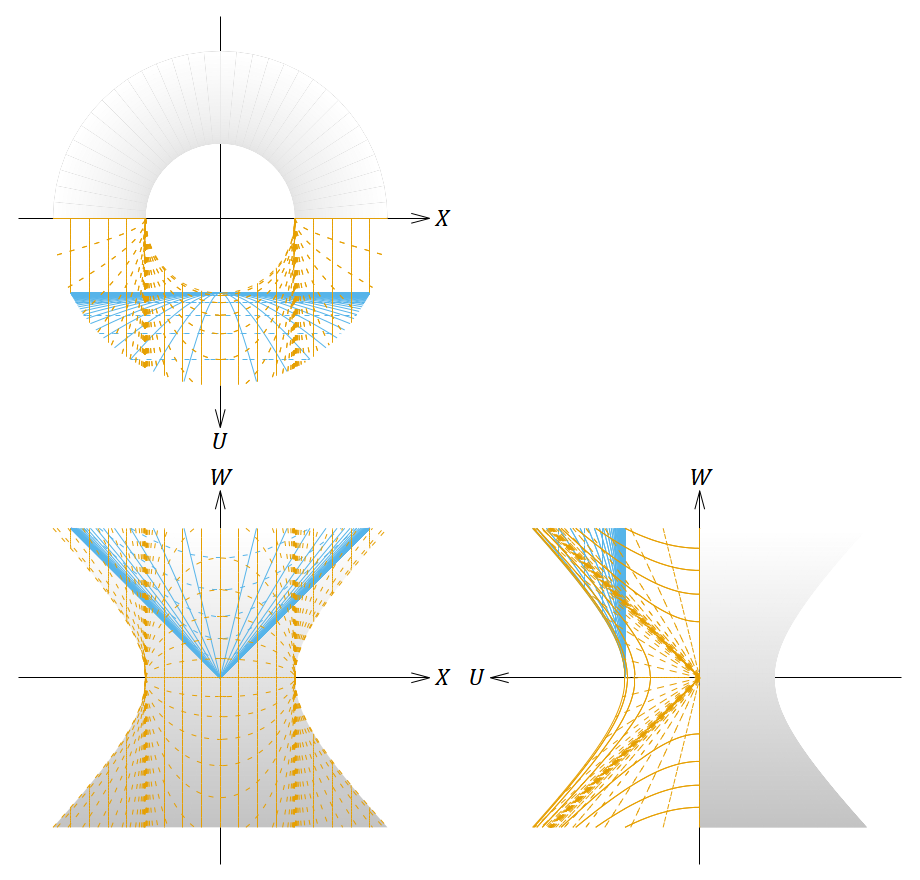
図15. 𝜌 < 𝐿 において静的な座標系と 𝑘 < 0 のFLRW計量(表2の④で複号が正)の座標系を張った4次元ドジッター時空を5次元ミンコフスキー時空に埋め込んだ図。
1番目の図は斜めから見た図、2〜4番目の図は正投影図である。茶色の線は 𝜌 < 𝐿 において静的な座標系、青色の線はFLRW計量の座標系を表す。
図15は茶色の座標系については1セット分だけ座標系を張り、残りの領域は塗りつぶしてある。時空全体を半分に分ける境界を図13と同じ斜めでなく図11と同じ縦にしてあるのはたまたまであり、特に意味はない。図15だけを見ると青色の座標系は時空全体の¼より小さい領域を覆っているようにも見えるが、割合で表すのは難しそうである。同じ形の座標系を何セットか持ってきて過不足なく時空全体を覆うことはできないように思える。
以上をまとめると、5次元ミンコフスキー時空に埋め込んだ4次元ドジッター時空に座標系を張る際、 𝑊 が一定となる面を同時刻とみなした座標系が 𝑘 > 0 のFLRW計量、 ± 𝑊 + 𝑈 が一定となる面を同時刻とみなした座標系が 𝑘 = 0 のFLRW計量、 𝑈 が一定となる面を同時刻とみなした座標系が 𝑘 < 0 のFLRW計量である。確かに座標系の張り方によって空間部分が開いたり閉じたりしているし、膨張や収縮しているように見せることもできる。
ではもっと中途半端な角度の面が同時刻になるように座標系を張ったらどうなるのだろうか。その場合でも上記と同じ 𝑘 ≷ 0 のFLRW計量になるのだ。この記事ではここまで一貫して、 𝑘 ≷ 0 の場合は 𝑤 = 0 なら 𝑣 = 0 になるように座標変換を定義してきた。しかし 𝑣 座標は並進対称性をもっているから 𝑣 は0でなくても何でもよいのである。 𝑤 = 0 に対応する 𝑣 の値を動かしていけば、同時刻面(𝑤 一定面)が5次元ミンコフスキー時空内で傾いていく(なお、その際に 𝑘 の値は変わらない。 𝑘 の(符号を変えずに)値を変えることは、 𝑟 座標の目盛り間隔を変えることに相当する)。あるいは別の考え方として、青色の座標系と茶色の座標系の座標変換は変えずに、茶色の座標系の埋め込み方を変えたと考えることもできる。(151)〜(154)式を少し変形して、 𝑣 に定数を足すように変更すればよい。そうすれば 𝑤 一定面が傾く。その定数を連続的に変化させた様子が図16である。実は 𝑣 方向の平行移動は 𝑊–𝑈 座標に対するローレンツ変換と同じ計算になっている。
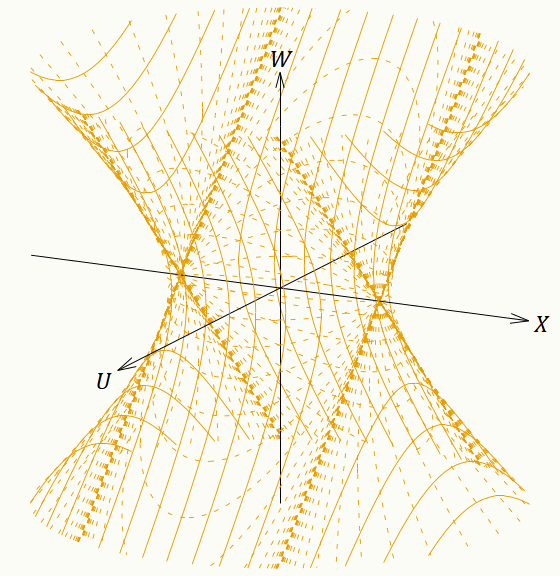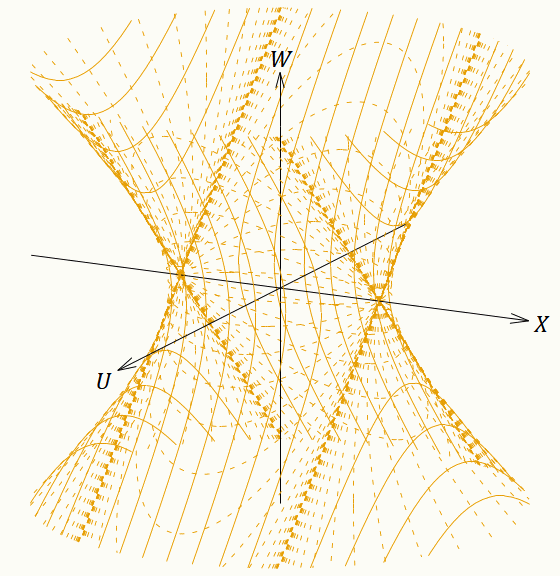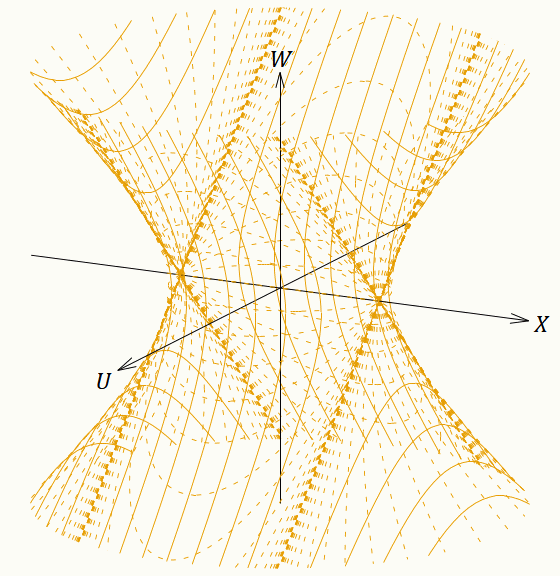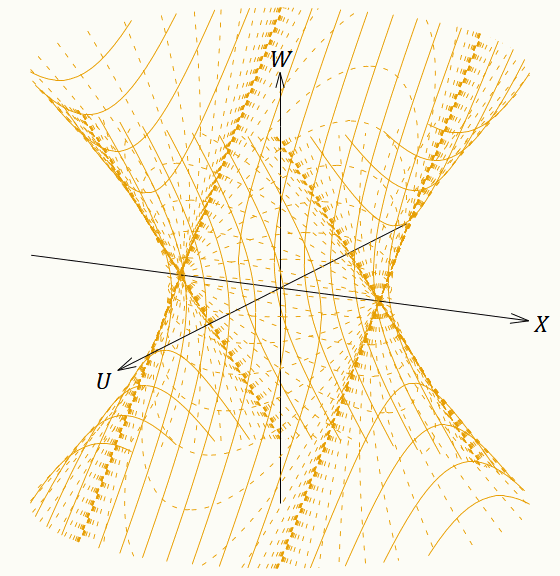
図16を見ると、 𝑣 の値がどれだけ変わっても、すなわちいくら時間が経過しても、状況は何も変わらないことがよくわかる。茶色の座標系を使う観測者にとって、大文字の座標系の原点(そこはドジッター時空の外であるが)はいつでも「現在」である。