2.2.1 空間の曲率がゼロの場合
平坦な空間(𝑘 = 0)である⑤の解
を最初に考える。これは複号が正なら加速膨張、負なら減速収縮である。この先このページでは最下行までずっと複号同順である。ここで動径座標に関して
という座標変換をする。このとき逆変換は
であり、その微分は
のようになる。これらを2乗すれば
である。(25)式を変形し(28)・(29)式を代入して座標変換後の線素の式を計算すると、
となる。この計量は 𝑤 に依存せず定常であるが、非対角成分である d𝑤d𝜌 の項があってわかりにくいので、計量が対角になるようにさらなる座標変換を考える。動径座標はもういじりたくないので、時間座標を座標変換することで対角計量を目指そう。新しい時間座標を 𝑣 として、今のところ未知のその変換と逆変換を
のように書く。すると、
であるから、これらを(30)式に代入すると
となる。ここで d𝑣d𝜌 の係数を0にすればよいのだが、
では困る(まともな座標変換にならない)から、
のようにすればよい。この偏微分方程式はボケっとしていると何が独立変数で何が従属変数なのか忘れそうになるので、括弧内に独立変数を明記しておいた。これを満たすような座標変換をすればよいのだが、 𝑓(𝑣) は任意と言われても手掛かりがなさ過ぎて困ってしまう。そこで、なるべく簡単になるように、特に根拠はないが試しに空間原点(𝜌 = 0)で恒等変換になるように 𝑓(𝑣) = 𝑣 としてみよう。そうすれば
となる。
(33)式より
である。(32)・(35)式を(31)式に代入して座標変換後の線素の式を計算すると、
となる。 を代入すれば、
となる。これは「宇宙項があったらシュバルツシルト解はどう変わるか」の記事で出てきたドジッター解と同じものである。これのことを「ドジッター時空」(de Sitter spacetime)とも呼ぶ。この計量は 𝜌 < 𝐿 において静的である。平坦な空間が加速膨張/減速収縮していると思っていた⑤の解は、ドジッター時空と同じものだったのだ。
ここでは2段階で座標変換をしたが、最初の座標系と最後の座標系が結局どういう関係になっているのかを求めると座標変換は
であり、逆変換は
である。
ただし 𝜌 = 𝐿 の領域ではこれらの変換式が使えない。その領域は元の座標系で考えれば(26)・(27)式より
ということになるが、この関係を満たす 𝑤 と 𝑟 を(38)式に代入すると新しい座標系では 𝑣 → ±∞ となって無限の未来/過去に飛ばされてしまう。逆に新しい座標系における 𝜌 = 𝐿 を元の座標系に変換するために(33)・(39)式に代入すると 𝑤 → ∓∞ , 𝑟 → +∞ となって無限の過去/未来の無限遠に飛ばされてしまう。だから 𝜌 = 𝐿 となる線上(4次元時空内で考えれば3次元超曲面上)の領域に限りこの座標変換は諦めることにする。
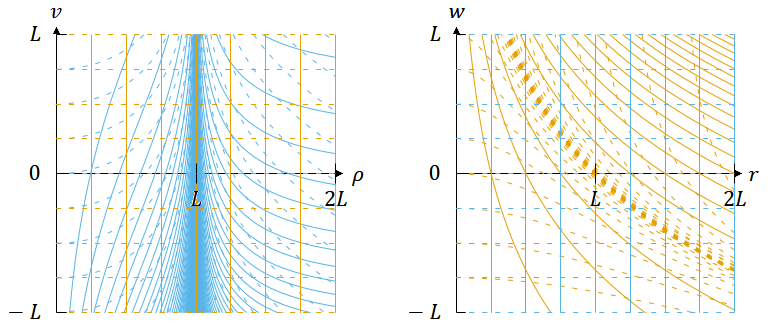
以上の関係を図示したものが図3・4である。茶色で描かれた座標系(𝜌 < 𝐿 において静的; (36)式)と青色で描かれた座標系(𝑘 = 0 のFLRW計量; (25)式)は、 𝜌 = 𝐿 の領域を除いて一対一に対応する。
図3. スケール因子を
としたFLRW計量(表1の⑤で複号が正)の座標変換。
茶色の線は 𝜌 < 𝐿 において静的な座標系、青色の線はFLRW計量の座標系を表す。
左図で青色の線が密集している 𝜌 = 𝐿 の線上の領域は、青色の座標系に対応する領域がない。右図で茶色の破線が密集している
の線上の領域は、茶色の座標系に対応する領域がない。これらの線上を除いて2つの座標系は一対一に対応する。
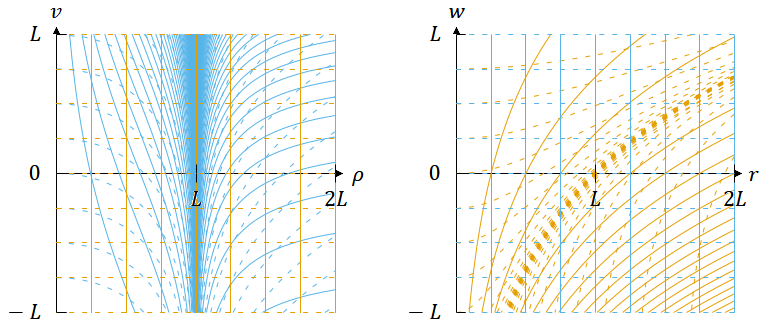
図4. スケール因子を
としたFLRW計量(表1の⑤で複号が負)の座標変換。
茶色の線は 𝜌 < 𝐿 において静的な座標系、青色の線はFLRW計量の座標系を表す。
左図で青色の線が密集している 𝜌 = 𝐿 の線上の領域は、青色の座標系に対応する領域がない。右図で茶色の破線が密集している
の線上の領域は、茶色の座標系に対応する領域がない。これらの線上を除いて2つの座標系は一対一に対応する。