2.2.3 空間の曲率が正の場合

表1で宇宙定数 𝛬 が正の場合の解は④〜⑥である。その中で空間の曲率が正である⑥の解 $$\begin{array}{ll}𝑎=\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}& \text{(71)}\\ {\mathrm{d𝑠}}^2=-{\mathrm{d𝑤}}^2+{\left(\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}\right)}^2(\frac{1}{1-𝑘{𝑟}^2}{\mathrm{d𝑟}}^2+{𝑟}^2{\mathrm{d𝜃}}^2+{𝑟}^2{\sin }^2𝜃{\mathrm{d𝜑}}^2)& \text{(72)}\end{array}$$ をここでは考える。これは減速収縮から加速膨張に転じる時空である。ここで動径座標に関して $$\begin{array}{lll}\hfill 𝑟\text{→}𝜌& =& 𝑎𝑟\\ & =& 𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}& \text{(73)}\end{array}$$ という座標変換をする。このとき逆変換は $$\begin{array}{llll}\hfill 𝜌\text{→}𝑟& =& \frac{𝜌}{\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}}& \text{(74)}\end{array}$$ であり、その微分は $$\begin{array}{lll}\hfill \mathrm{d𝑟}& =& \frac{\mathrm{\partial 𝑟}}{\mathrm{\partial 𝑤}}\mathrm{d𝑤}+\frac{\mathrm{\partial 𝑟}}{\mathrm{\partial 𝜌}}\mathrm{d𝜌}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿}(-\frac{\sinh \frac{𝑤}{𝐿}}{{\cosh }^2\frac{𝑤}{𝐿}}\cdot \frac{1}{𝐿})\mathrm{d𝑤}+\frac{1}{\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}}\mathrm{d𝜌}\\ & =& \frac{1}{\sqrt{𝑘}𝐿{\cosh }^2\frac{𝑤}{𝐿}}(-\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\mathrm{d𝑤}+\cosh \frac{𝑤}{𝐿}\mathrm{d𝜌})\end{array}$$ のようになる。これらを2乗すれば $$\begin{array}{llll}\hfill {𝑟}^2& =& \frac{{𝜌}^2}{𝑘{𝐿}^2{\cosh }^2\frac{𝑤}{𝐿}}& \text{(75)}\\ \hfill {\mathrm{d𝑟}}^2& =& \frac{1}{𝑘{𝐿}^2{\cosh }^4\frac{𝑤}{𝐿}}(\frac{{𝜌}^2}{{𝐿}^2}{\sinh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2)& \text{(76)}\end{array}$$ である。(72)式を変形し(75)・(76)式を代入して座標変換後の線素の式を計算すると、 $$\begin{array}{lll}\hfill {\mathrm{d𝑠}}^2& =& -{\mathrm{d𝑤}}^2+𝑘{𝐿}^2\left({\cosh }^2\frac{𝑤}{𝐿}\right)(\frac{1}{1-𝑘{𝑟}^2}{\mathrm{d𝑟}}^2+{𝑟}^2{\mathrm{d𝜃}}^2+{𝑟}^2{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& -{\mathrm{d𝑤}}^2+\frac{𝑘{𝐿}^2{\cosh }^2\frac{𝑤}{𝐿}}{1-𝑘{𝑟}^2}{\mathrm{d𝑟}}^2+𝑘{𝐿}^2\left({\cosh }^2\frac{𝑤}{𝐿}\right){𝑟}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& -{\mathrm{d𝑤}}^2+\frac{𝑘{𝐿}^2{\cosh }^2\frac{𝑤}{𝐿}}{1-𝑘\cdot \frac{{𝜌}^2}{𝑘{𝐿}^2{\cosh }^2\frac{𝑤}{𝐿}}}\cdot \frac{1}{𝑘{𝐿}^2{\cosh }^4\frac{𝑤}{𝐿}}(\frac{{𝜌}^2}{{𝐿}^2}{\sinh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2)\\ & & +𝑘{𝐿}^2\left({\cosh }^2\frac{𝑤}{𝐿}\right)\frac{{𝜌}^2}{𝑘{𝐿}^2{\cosh }^2\frac{𝑤}{𝐿}}({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& -{\mathrm{d𝑤}}^2+\frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}(\frac{{𝜌}^2}{{𝐿}^2}{\sinh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2)\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\{-({\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}){\mathrm{d𝑤}}^2+\frac{{𝜌}^2}{{𝐿}^2}{\sinh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2\}\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\left[\right\{-{\cosh }^2\frac{𝑤}{𝐿}+\frac{{𝜌}^2}{{𝐿}^2}(1+{\sinh }^2\frac{𝑤}{𝐿})\}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2]\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\left\{\right(-{\cosh }^2\frac{𝑤}{𝐿}+\frac{{𝜌}^2}{{𝐿}^2}{\cosh }^2\frac{𝑤}{𝐿}){\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2\}\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2\}\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)& \text{(77)}\end{array}$$ となる。これは計量の非対角成分である d𝑤d𝜌 の項があってわかりにくいので、計量が対角になるようにさらなる座標変換を考える。動径座標はもういじりたくないので、時間座標を座標変換することで対角計量を目指そう。新しい時間座標を 𝑣 として、今のところ未知のその変換と逆変換を $$\begin{array}{lll}\hfill 𝑤& \text{→}& 𝑣=𝑣(𝑤,𝜌)\\ \hfill 𝑣& \text{→}& 𝑤=𝑤(𝑣,𝜌)\end{array}$$ のように書く。すると、 $$\begin{array}{lll}\hfill \mathrm{d𝑤}& =& \frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\mathrm{d𝑣}+\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\mathrm{d𝜌}\\ \hfill {\mathrm{d𝑤}}^2& =& {\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\right)}^2{\mathrm{d𝑣}}^2+2\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\mathrm{d𝑣}\mathrm{d𝜌}+{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\right)}^2{\mathrm{d𝜌}}^2\end{array}$$ であるから、これらを(77)式に代入すると $$\begin{array}{lll}\hfill {\mathrm{d𝑠}}^2& =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝑤}}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\mathrm{d𝑤}\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2\}\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}[-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}\{{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\right)}^2{\mathrm{d𝑣}}^2+2\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\mathrm{d𝑣}\mathrm{d𝜌}+{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\right)}^2{\mathrm{d𝜌}}^2\}\\ & & -2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\mathrm{d𝑣}+\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\mathrm{d𝜌})\mathrm{d𝜌}+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2]\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}[-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\right)}^2{\mathrm{d𝑣}}^2-2(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\mathrm{d𝑣}\mathrm{d𝜌}-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\right)}^2{\mathrm{d𝜌}}^2\\ & & -2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\mathrm{d𝑣}\mathrm{d𝜌}-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}{\mathrm{d𝜌}}^2+{\cosh }^2\frac{𝑤}{𝐿}{\mathrm{d𝜌}}^2]\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)\\ & =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}[-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\right)}^2{\mathrm{d𝑣}}^2-2\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\{(1-\frac{{𝜌}^2}{{𝐿}^2})\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}+\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\}\mathrm{d𝑣}\mathrm{d𝜌}\\ & & +\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\right)}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}+{\cosh }^2\frac{𝑤}{𝐿}\}{\mathrm{d𝜌}}^2]\\ & & +{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)& \text{(78)}\end{array}$$ となる。ここで d𝑣d𝜌 の係数を0にすればよいのだが、 $\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}=0$ では困る（まともな座標変換にならない）から、 $$\begin{array}{lll}\hfill (1-\frac{{𝜌}^2}{{𝐿}^2})\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}+\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}& =& 0\\ \hfill (1-\frac{{𝜌}^2}{{𝐿}^2})\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}& =& -\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\\ \hfill \frac{\cosh \frac{𝑤}{𝐿}}{𝐿\sinh \frac{𝑤}{𝐿}}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}& =& -\frac{𝜌}{{𝐿}^2(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ \hfill \frac{\partial }{\mathrm{\partial 𝜌}}\ln \left|\sinh \frac{𝑤}{𝐿}\right|& =& \frac{\partial }{\mathrm{\partial 𝜌}}\left(\frac{1}{2}\ln |1-\frac{{𝜌}^2}{{𝐿}^2}|\right)\\ \hfill \ln \left|\sinh \frac{𝑤}{𝐿}\right|& =& \frac{1}{2}\ln |1-\frac{{𝜌}^2}{{𝐿}^2}|+𝑓\left(𝑣\right)& \text{（𝑓(𝑣)は𝑣の任意関数）}\\ \hfill \sinh \frac{𝑤}{𝐿}& =& \pm \sqrt{|1-\frac{{𝜌}^2}{{𝐿}^2}|}{\mathrm{e}}^{𝑓\left(𝑣\right)}& \text{(79)}\end{array}$$ を満たすような座標変換をすればよい。ここで表記の簡略化のために $$\begin{array}{l}𝐴\left(𝜌\right)=\sqrt{|1-\frac{{𝜌}^2}{{𝐿}^2}|}\\ 𝐵\left(𝑣\right)=\pm {\mathrm{e}}^{𝑓\left(𝑣\right)}\end{array}$$ と置く。後で使うために場合分けをして 𝐴(𝜌) を 𝜌 で微分すると、 $$\begin{array}{ll}𝐴\left(𝜌\right)=\{\begin{array}{ll}\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}& (0\leqq 𝜌<𝐿)\\ \sqrt{-(1-\frac{{𝜌}^2}{{𝐿}^2})}& (𝐿<𝜌)\end{array}& \text{(80)}\\ \frac{\mathrm{d𝐴}\left(𝜌\right)}{\mathrm{d𝜌}}=\{\begin{array}{ll}-\frac{\frac{𝜌}{{𝐿}^2}}{\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}}& (0\leqq 𝜌<𝐿)\\ \frac{\frac{𝜌}{{𝐿}^2}}{\sqrt{-(1-\frac{{𝜌}^2}{{𝐿}^2})}}& (𝐿<𝜌)\end{array}& \text{(81)}\end{array}$$ である。このとき(79)式より $$\begin{array}{llll}\hfill \sinh \frac{𝑤}{𝐿}& =& 𝐴\left(𝜌\right)𝐵\left(𝑣\right)& \text{(82)}\\ \hfill 𝑤& =& 𝐿\mathrm{arsinh}\left\{𝐴\right(𝜌\left)𝐵\right(𝑣\left)\right\}& \text{(83)}\end{array}$$ と書ける。

𝐵(𝑣) は任意の関数であって具体的な形が未定であるが、それは後で決めることにしてとりあえずこのまま計算を進める。ここからは 𝐴 や 𝐵 の引数を表す (𝜌) や (𝑣) は省略する。(82)式より $$\begin{array}{lll}\hfill {\sinh }^2\frac{𝑤}{𝐿}& =& {𝐴}^2{𝐵}^2\\ \hfill {\cosh }^2\frac{𝑤}{𝐿}& =& {\sinh }^2\frac{𝑤}{𝐿}+1\\ & =& {𝐴}^2{𝐵}^2+1& \text{(84)}\\ \hfill \cosh \frac{𝑤}{𝐿}& =& \sqrt{{𝐴}^2{𝐵}^2+1}& \text{(85)}\end{array}$$ であり、(83)式より $$\begin{array}{lll}\hfill \frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}& =& 𝐿\frac{1}{\sqrt{{\left(𝐴𝐵\right)}^2+1}}\frac{\partial }{\mathrm{\partial 𝑣}}\left(𝐴𝐵\right)\\ & =& \frac{𝐿𝐴\dot{𝐵}}{\sqrt{{𝐴}^2{𝐵}^2+1}}& \text{(86)}\\ \hfill \frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}& =& 𝐿\frac{1}{\sqrt{{\left(𝐴𝐵\right)}^2+1}}\frac{\partial }{\mathrm{\partial 𝜌}}\left(𝐴𝐵\right)\\ & =& \frac{𝐿{𝐴}^{\prime }𝐵}{\sqrt{{𝐴}^2{𝐵}^2+1}}& \text{(87)}\end{array}$$ である。ただしドット ˙ は座標 𝑣 による微分 $\frac{\mathrm{d}}{\mathrm{d𝑣}}$ を表し、プライム ′ は座標 𝜌 による微分 $\frac{\mathrm{d}}{\mathrm{d𝜌}}$ を表す。(82)・(84)〜(87)式を(78)式に代入して座標変換後の線素の式を計算したいが、(78)式はかなり長くなっているので一気に代入すると大変である。そこで計量の成分ごとに計算しよう。

(78)式の d𝑣^² の係数は $$\begin{array}{lll}\hfill {𝑔}_{00}& =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝑣}}\right)}^2\}\\ & =& \frac{1}{({𝐴}^2{𝐵}^2+1)-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐴}^2{𝐵}^2+1){\left(\frac{𝐿𝐴\dot{𝐵}}{\sqrt{{𝐴}^2{𝐵}^2+1}}\right)}^2\}\\ & =& \frac{1}{{𝐴}^2{𝐵}^2+1-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐴}^2{𝐵}^2+1)\frac{{𝐿}^2{𝐴}^2{\dot{𝐵}}^2}{{𝐴}^2{𝐵}^2+1}\}\\ & =& \frac{1}{{𝐴}^2{𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2{𝐴}^2{\dot{𝐵}}^2\}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{𝐴}^2{\dot{𝐵}}^2}{{𝐴}^2{𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+\frac{1}{{𝐴}^2}(1-\frac{{𝜌}^2}{{𝐿}^2})}\end{array}$$ である。ここに(80)式を代入すると、 0 ≦ 𝜌 < 𝐿 の領域では $$\begin{array}{lll}\hfill {𝑔}_{(+)00}& =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+\frac{1}{{𝐴}^2}(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+\frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+1}\end{array}$$ となり、 𝐿 < 𝜌 の領域では $$\begin{array}{lll}\hfill {𝑔}_{(-)00}& =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+\frac{1}{{𝐴}^2}(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+\frac{1}{-(1-\frac{{𝜌}^2}{{𝐿}^2})}(1-\frac{{𝜌}^2}{{𝐿}^2})}\\ & =& -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2-1}\end{array}$$ となる。まとめると $${𝑔}_{00}=\{\begin{array}{ll}-(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+1}& (0\leqq 𝜌<𝐿)\\ -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2-1}& (𝐿<𝜌)\end{array}$$ のようになる。

(78)式の d𝑣d𝜌 の係数は、それが0になるように 𝑣 を決めたのだから当然0である。

(78)式の d𝜌^² の係数は $$\begin{array}{lll}\hfill {𝑔}_{11}& =& \frac{1}{{\cosh }^2\frac{𝑤}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑤}{𝐿}{\left(\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}\right)}^2-2\frac{𝜌}{𝐿}\sinh \frac{𝑤}{𝐿}\cosh \frac{𝑤}{𝐿}\frac{\mathrm{\partial 𝑤}}{\mathrm{\partial 𝜌}}+{\cosh }^2\frac{𝑤}{𝐿}\}\\ & =& \frac{1}{({𝐴}^2{𝐵}^2+1)-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐴}^2{𝐵}^2+1){\left(\frac{𝐿{𝐴}^{\prime }𝐵}{\sqrt{{𝐴}^2{𝐵}^2+1}}\right)}^2-2\frac{𝜌}{𝐿}𝐴𝐵\sqrt{{𝐴}^2{𝐵}^2+1}\frac{𝐿{𝐴}^{\prime }𝐵}{\sqrt{{𝐴}^2{𝐵}^2+1}}+({𝐴}^2{𝐵}^2+1)\}\\ & =& \frac{1}{{𝐴}^2{𝐵}^2+1-\frac{{𝜌}^2}{{𝐿}^2}}\{-(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐴}^2{𝐵}^2+1)\frac{{𝐿}^2{{𝐴}^{\prime }}^2{𝐵}^2}{{𝐴}^2{𝐵}^2+1}-2\frac{𝜌}{𝐿}𝐴𝐵\cdot 𝐿{𝐴}^{\prime }𝐵+{𝐴}^2{𝐵}^2+1\}\\ & =& \frac{1}{{𝐴}^2{𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2{{𝐴}^{\prime }}^2{𝐵}^2-2𝜌𝐴{𝐴}^{\prime }{𝐵}^2+{𝐴}^2{𝐵}^2+1\}\end{array}$$ である。ここに(80)・(81)式を代入すると、 0 ≦ 𝜌 < 𝐿 の領域では $$\begin{array}{lll}\hfill {𝑔}_{(+)11}& =& \frac{1}{{𝐴}^2{𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2{{𝐴}^{\prime }}^2{𝐵}^2-2𝜌𝐴{𝐴}^{\prime }{𝐵}^2+{𝐴}^2{𝐵}^2+1\}\\ & =& \frac{1}{(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2\frac{\frac{{𝜌}^2}{{𝐿}^4}}{1-\frac{{𝜌}^2}{{𝐿}^2}}{𝐵}^2-2𝜌\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}(-\frac{\frac{𝜌}{{𝐿}^2}}{\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}}){𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐵}^2+1\}\\ & =& \frac{1}{(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐵}^2+1)}(-\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2+2\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2+{𝐵}^2-\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2+1)\\ & =& \frac{1}{(1-\frac{{𝜌}^2}{{𝐿}^2})({𝐵}^2+1)}({𝐵}^2+1)\\ & =& \frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}\end{array}$$ となり、 𝐿 < 𝜌 の領域では $$\begin{array}{lll}\hfill {𝑔}_{(-)11}& =& \frac{1}{{𝐴}^2{𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2{{𝐴}^{\prime }}^2{𝐵}^2-2𝜌𝐴{𝐴}^{\prime }{𝐵}^2+{𝐴}^2{𝐵}^2+1\}\\ & =& \frac{1}{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐵}^2+(1-\frac{{𝜌}^2}{{𝐿}^2})}\{-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐿}^2\frac{\frac{{𝜌}^2}{{𝐿}^4}}{-(1-\frac{{𝜌}^2}{{𝐿}^2})}{𝐵}^2-2𝜌\sqrt{-(1-\frac{{𝜌}^2}{{𝐿}^2})}\cdot \frac{\frac{𝜌}{{𝐿}^2}}{\sqrt{-(1-\frac{{𝜌}^2}{{𝐿}^2})}}{𝐵}^2-(1-\frac{{𝜌}^2}{{𝐿}^2}){𝐵}^2+1\}\\ & =& \frac{1}{(1-\frac{{𝜌}^2}{{𝐿}^2})(-{𝐵}^2+1)}(\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2-2\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2-{𝐵}^2+\frac{{𝜌}^2}{{𝐿}^2}{𝐵}^2+1)\\ & =& \frac{1}{(1-\frac{{𝜌}^2}{{𝐿}^2})(-{𝐵}^2+1)}(-{𝐵}^2+1)\\ & =& \frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}\end{array}$$ となる。したがってどちらの領域でも $${𝑔}_{11}=\frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}$$ のようになる。

これら以外の計量の成分は座標変換しても変わらない。以上により線素の式は $${\mathrm{d𝑠}}^2=\{\begin{array}{ll}-(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+1}{\mathrm{d𝑣}}^2+\frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}{\mathrm{d𝜌}}^2+{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)& (0\leqq 𝜌<𝐿)\\ -(1-\frac{{𝜌}^2}{{𝐿}^2})\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2-1}{\mathrm{d𝑣}}^2+\frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}{\mathrm{d𝜌}}^2+{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)& (𝐿<𝜌)\end{array}\text{(88)}$$ となる。あとは 𝐵(𝑣) の形を好きなように決めればよいのだが、ここで仮に 𝑔_₀₀ が 𝑣 を含まなければ静的な計量にすることができて良さそうである。そのためには $\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2+1}=1$ とか $\frac{{𝐿}^2{\dot{𝐵}}^2}{{𝐵}^2-1}=1$ という微分方程式を解けばよい（右辺は正の定数なら何でもよいが、1にしておくのが楽である）。これらは両辺の平方根を 𝑣 で積分するだけで解けるので計算過程を省略していきなり答えを書くと、 $$𝐵\left(𝑣\right)=\{\begin{array}{ll}\sinh \frac{𝑣}{𝐿}& (0\leqq 𝜌<𝐿)\\ \pm \cosh \frac{𝑣}{𝐿}& (𝐿<𝜌)\end{array}\text{(89)}$$ である。下側の式についている複号は 𝑤 と 𝑣 の符号が同じになるように変換することと定義しておく。(89)式を(88)式に代入すれば $$\begin{array}{llll}\hfill {\mathrm{d𝑠}}^2& =& -(1-\frac{{𝜌}^2}{{𝐿}^2}){\mathrm{d𝑣}}^2+\frac{1}{1-\frac{{𝜌}^2}{{𝐿}^2}}{\mathrm{d𝜌}}^2+{𝜌}^2({\mathrm{d𝜃}}^2+{\sin }^2𝜃{\mathrm{d𝜑}}^2)& \text{(90)}\end{array}$$ となる。この計量は⑤の解（平坦な空間のFLRW計量）を座標変換した(36)式と同じであり、 𝜌 < 𝐿 において静的である。曲率が正の空間が減速収縮から加速膨張に転じると思っていた⑥の解は、ドジッター時空と同じものだったのだ。

ここでは2段階で座標変換をしたが、最初の座標系と最後の座標系が結局どういう関係になっているのかを求めておこう。

0 ≦ 𝜌 < 𝐿 の領域では、(80)・(89)式を(83)・(82)式に代入すると、 $$\begin{array}{llll}\hfill 𝑤& =& 𝐿\mathrm{arsinh}\left(\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}\sinh \frac{𝑣}{𝐿}\right)& \text{(91)}\\ \hfill \sinh \frac{𝑤}{𝐿}& =& \sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}\sinh \frac{𝑣}{𝐿}& \text{(92)}\\ \hfill \frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}}& =& \sinh \frac{𝑣}{𝐿}\\ \hfill 𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}}& =& 𝑣& \text{(93)}\end{array}$$ であるから、座標変換は $$\begin{array}{llll}𝑣& =& 𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}}& \text{←}\text{(93)式}\\ & =& 𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-\frac{{\left(𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}\right)}^2}{{𝐿}^2}}}& \text{←}\text{(73)式}\text{を代入した。}\\ & =& 𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-\frac{{𝐿}^2𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}{{𝐿}^2}}}\\ & =& 𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}}\\ 𝜌& =& 𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}& \text{←}\text{(73)式}\end{array}$$ であり、逆変換は $$\begin{array}{llll}𝑤& =& 𝐿\mathrm{arsinh}\left(\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}\sinh \frac{𝑣}{𝐿}\right)& \text{←}\text{(91)式}\\ 𝑟& =& \frac{𝜌}{\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}}& \text{←}\text{(74)式}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{{\sinh }^2\frac{𝑤}{𝐿}+1}}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{{\left(\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}\sinh \frac{𝑣}{𝐿}\right)}^2+1}}& \text{←}\text{(92)式}\text{を代入した。}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{(1-\frac{{𝜌}^2}{{𝐿}^2}){\sinh }^2\frac{𝑣}{𝐿}+1}}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{{\cosh }^2\frac{𝑣}{𝐿}-\frac{{𝜌}^2}{{𝐿}^2}{\sinh }^2\frac{𝑣}{𝐿}}}\\ & =& \frac{𝜌}{\sqrt{𝑘}\sqrt{{𝐿}^2{\cosh }^2\frac{𝑣}{𝐿}-{𝜌}^2{\sinh }^2\frac{𝑣}{𝐿}}}\end{array}$$ である。

𝐿 < 𝜌 の領域では、(80)・(89)式を(83)・(82)式に代入すると、 $$\begin{array}{llll}\hfill 𝑤& =& 𝐿\mathrm{arsinh}(\pm \sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿})& \text{(94)}\\ \hfill \sinh \frac{𝑤}{𝐿}& =& \pm \sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿}& \text{(95)}\\ \hfill \pm \frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}}& =& \cosh \frac{𝑣}{𝐿}\\ \hfill \pm 𝐿\mathrm{arcosh}\frac{\sinh \frac{\pm 𝑤}{𝐿}}{\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}}& =& 𝑣& \text{(96)}\end{array}$$ であるから、座標変換は $$\begin{array}{llll}𝑣& =& \pm 𝐿\mathrm{arcosh}\frac{\sinh \frac{\pm 𝑤}{𝐿}}{\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}}& \text{←}\text{(96)式}\\ & =& \pm 𝐿\mathrm{arcosh}\frac{\sinh \frac{\pm 𝑤}{𝐿}}{\sqrt{-1+\frac{{\left(𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}\right)}^2}{{𝐿}^2}}}& \text{←}\text{(73)式}\text{を代入した。}\\ & =& \pm 𝐿\mathrm{arcosh}\frac{\sinh \frac{\pm 𝑤}{𝐿}}{\sqrt{-1+\frac{{𝐿}^2𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}{{𝐿}^2}}}\\ & =& \pm 𝐿\mathrm{arcosh}\frac{\sinh \frac{\pm 𝑤}{𝐿}}{\sqrt{-1+𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}}\\ 𝜌& =& 𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}& \text{←}\text{(73)式}\end{array}$$ であり、逆変換は $$\begin{array}{llll}𝑤& =& 𝐿\mathrm{arsinh}(\pm \sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿})& \text{←}\text{(94)式}\\ & =& \pm 𝐿\mathrm{arsinh}\left(\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿}\right)\\ 𝑟& =& \frac{𝜌}{\sqrt{𝑘}𝐿\cosh \frac{𝑤}{𝐿}}& \text{←}\text{(74)式}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{{\sinh }^2\frac{𝑤}{𝐿}+1}}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{{(\pm \sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿})}^2+1}}& \text{←}\text{(95)式}\text{を代入した。}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{(-1+\frac{{𝜌}^2}{{𝐿}^2}){\cosh }^2\frac{𝑣}{𝐿}+1}}\\ & =& \frac{𝜌}{\sqrt{𝑘}𝐿\sqrt{\frac{{𝜌}^2}{{𝐿}^2}{\cosh }^2\frac{𝑣}{𝐿}-{\sinh }^2\frac{𝑣}{𝐿}}}\\ & =& \frac{𝜌}{\sqrt{𝑘}\sqrt{{𝜌}^2{\cosh }^2\frac{𝑣}{𝐿}-{𝐿}^2{\sinh }^2\frac{𝑣}{𝐿}}}\end{array}$$ である。

場合分けと式変形が長くなって全体が見づらいので結果だけをもう一度書いておくと、 $$\begin{array}{ll}𝑣=\{\begin{array}{ll}𝐿\mathrm{arsinh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{1-𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}}& (0\leqq 𝜌<\mathrm{𝐿})\\ 𝐿\mathrm{arcosh}\frac{\sinh \frac{𝑤}{𝐿}}{\sqrt{-1+𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}}& (\mathrm{𝐿}<𝜌,0<\mathrm{𝑣})\\ -𝐿\mathrm{arcosh}\frac{\sinh \frac{-𝑤}{𝐿}}{\sqrt{-1+𝑘{𝑟}^2{\cosh }^2\frac{𝑤}{𝐿}}}& (\mathrm{𝐿}<𝜌,𝑣<0)\end{array}& \text{(97)}\\ 𝜌=𝐿\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}& \text{(98)}\end{array}$$ $$\begin{array}{ll}𝑤=\{\begin{array}{ll}𝐿\mathrm{arsinh}\left(\sqrt{1-\frac{{𝜌}^2}{{𝐿}^2}}\sinh \frac{𝑣}{𝐿}\right)& (0\leqq 𝜌<\mathrm{𝐿})\\ 𝐿\mathrm{arsinh}\left(\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿}\right)& (\mathrm{𝐿}<𝜌,0<\mathrm{𝑣})\\ -𝐿\mathrm{arsinh}\left(\sqrt{-1+\frac{{𝜌}^2}{{𝐿}^2}}\cosh \frac{𝑣}{𝐿}\right)& (\mathrm{𝐿}<𝜌,𝑣<0)\end{array}& \text{(99)}\\ 𝑟=\{\begin{array}{ll}\frac{𝜌}{\sqrt{𝑘}\sqrt{{𝐿}^2{\cosh }^2\frac{𝑣}{𝐿}-{𝜌}^2{\sinh }^2\frac{𝑣}{𝐿}}}& (0\leqq 𝜌<\mathrm{𝐿})\\ \frac{𝜌}{\sqrt{𝑘}\sqrt{{𝜌}^2{\cosh }^2\frac{𝑣}{𝐿}-{𝐿}^2{\sinh }^2\frac{𝑣}{𝐿}}}& (\mathrm{𝐿}<𝜌)\end{array}& \text{(100)}\end{array}$$ である。まだ 𝜌 = 𝐿 の領域が残っているが、これはどうしようもない。その領域は元の座標系で考えれば(73)・(74)式より $\sqrt{𝑘}𝑟\cosh \frac{𝑤}{𝐿}=1$ ということになるが、この関係を満たす 𝑤 と 𝑟 を(97)式に代入すると、 𝑤 = 0 でない限り新しい座標系では 𝑣 → ±∞ となって無限の未来/過去に飛ばされてしまう。逆に新しい座標系における 𝜌 = 𝐿 を元の座標系に変換するために(99)・(100)式に代入すると 𝑣 にかかわらず $(𝑤,𝑟)=(0,\frac{1}{\sqrt{𝑘}})$ となり1点に集まってしまう。だから 𝜌 = 𝐿 となる線上（4次元時空内で考えれば3次元超曲面上）の領域に限りこの座標変換は諦めることにする。

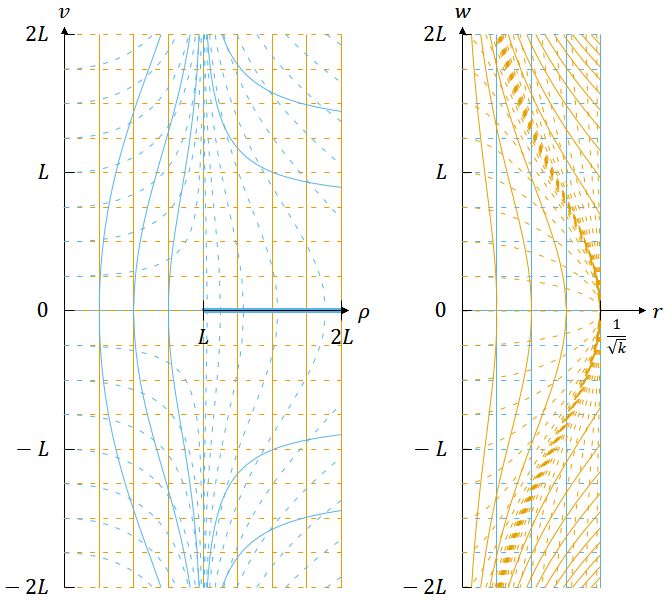
以上の関係を図示したものが図7である。茶色で描かれた座標系（𝜌 < 𝐿 において静的; (90)式）と青色で描かれた座標系（𝑘 > 0 のFLRW計量; (72)式）は、 𝜌 = 𝐿 の領域と 𝑣 = 0 (𝜌 > 𝐿) の領域を除いて一対一に対応する。後者の座標系は時空の半分の領域を覆うのだったから、前者の座標系も時空のほぼ半分の領域を覆っていることになる。

2.2.4 同じドジッター時空

表1で宇宙定数 𝛬 が正の場合の解である④〜⑥は実はすべて同じドジッター時空であることが2.2.1〜2.2.3節でわかった。座標系の張り方の違いによって3種類（複号を区別すれば5種類）あるように見えていただけだ。

確かに数式の上では座標変換でそうなることが示されたが、結局その時空はどのような形をしているか、これだけではよくわからない。 𝑘 < 0 は無限に開いた空間、 𝑘 > 0 は有限の閉じた空間である。座標変換するだけで本当に空間部分が開いたり閉じたりするものだろうか。また、 𝜌 = 𝐿 では座標変換がうまくいかないが、そこはどうなっているのか。さらに、図7の茶色の座標系では 𝑣 = 0 (𝜌 > 𝐿) のところで時空が切れていたが、図3・4の茶色の座標系ではどこにもそんな切れ目は存在しなかった。これは矛盾ではないのだろうか。

このようにいろいろ疑問がわいてくる。これについてはわかりやすく理解する方法があるので、あとで第3章で説明する。