第1章 フリードマン・ルメートル・ロバートソン・ウォーカー計量
これまでバーコフの定理の記事などで考えたように、原点に対して球対称な時空の計量は一般的に という形になるのだった。原点に対して球対称な時空であれば、普通は(1)式の 𝐴(𝑤, 𝑟) と 𝐵(𝑤, 𝑟) の2つをうまく調節すれば表現できるということだ。
ではもっと条件が厳しい一様・等方な時空の計量は一般的にどのような形になるのだろうか。
1.1 一様・等方な2次元空間の計量
最初から曲がった3次元空間を考えるのは大変なので、先に曲がった2次元空間の場合を考えよう。一様・等方な2次元空間といえば、最も単純なものは2次元ユークリッド平面である。そこに普通の極座標(動径座標 𝑟、角度座標 𝜑)を張った場合の線素の式は であることは言うまでもない。
ユークリッド平面の他に、球面も一様・等方な2次元空間である。3次元ユークリッド空間に埋め込まれた半径 𝐷 の2次元球面に普通の球面座標(緯度 𝜃 (北極が0)、経度 𝜑)を張った場合の線素の式は である。ここで、図1のように 𝑧 軸からの距離を 𝑟 として、 𝜃 の代わりに 𝑟 を使った座標系に座標変換することを考える。このような座標系を採用すると北半球と南半球のどちらか一方しか表現できなくなることには注意が必要である。なぜならばまったく同じ座標値になる点が北半球と南半球にそれぞれ1か所ずつ存在するからである。
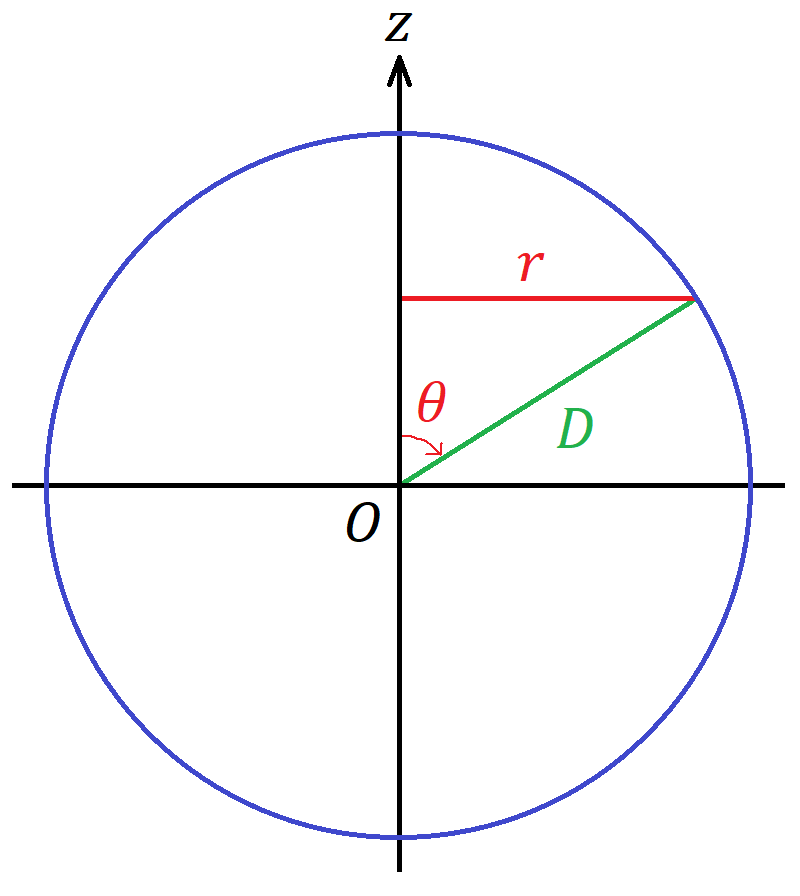
図1からわかるように である。(5)式の微分を計算すると となる。複号は北半球なら正、南半球なら負である。そして(6)・(7)式を(3)式に代入すると、 のようになる。ただし曲率として と置いた。
ここで(2)式と(8)式を見比べてみると、(8)式の 𝑘 を0にすれば(2)式になるので、(8)式だけで両方の場合を言い表せていることがわかる。曲率 𝑘 が正なら球面、0なら平面というわけである。それならば 𝑘 が負の場合も考えられるのではないか、ということでその場合は擬球面になる。擬球面については説明を省略するので、気になる人は他の本等を見てほしい。
結局、(8)式が一様・等方な2次元空間の計量の一般形である。上の方の書いたように、 𝑘 が正のときはこの座標系では空間の半分の領域しかカバーできない。 𝑘 が0以下のときは空間の全域をカバーできる。
1.2 一様・等方な3次元空間の計量
2次元で考えたことを踏まえて、次は3次元について考える。一様・等方な3次元空間といえば、最も単純なものは3次元ユークリッド空間である。そこに普通の球座標(𝑟, 𝜃, 𝜑)を張った場合の線素の式は であることは言うまでもない。ここで、2次元のときに(2)式を一般化したら(8)式の形になったのと同じように、(9)式を少し書き換えて という計量を考えてみると、実はこれが一様・等方な3次元空間の計量の一般形である。これで良い理由をこれ以上は当記事で説明しないので、詳しいことは教科書等を見てほしい。
(10)式の 𝑘 が0なら3次元ユークリッド空間、 𝑘 が正なら3次元超球面、 𝑘 が負なら3次元超擬球面である。 𝑘 が正のときはこの座標系では空間の半分の領域しかカバーできず、 𝑘 が0以下ならばそのような制限はないことも、2次元のときと同様である。
3次元超球面
3次元超球面は閉じた3次元空間であって、有限であるが端はない。3次元世界の人間が3次元超球面を思い浮かべることは難しいが、まったくイメージがわかないのは不便である。そこで、2次元世界の人間が2次元球面を想像する手順を参考にして3次元超球面を思い浮かべてみよう。
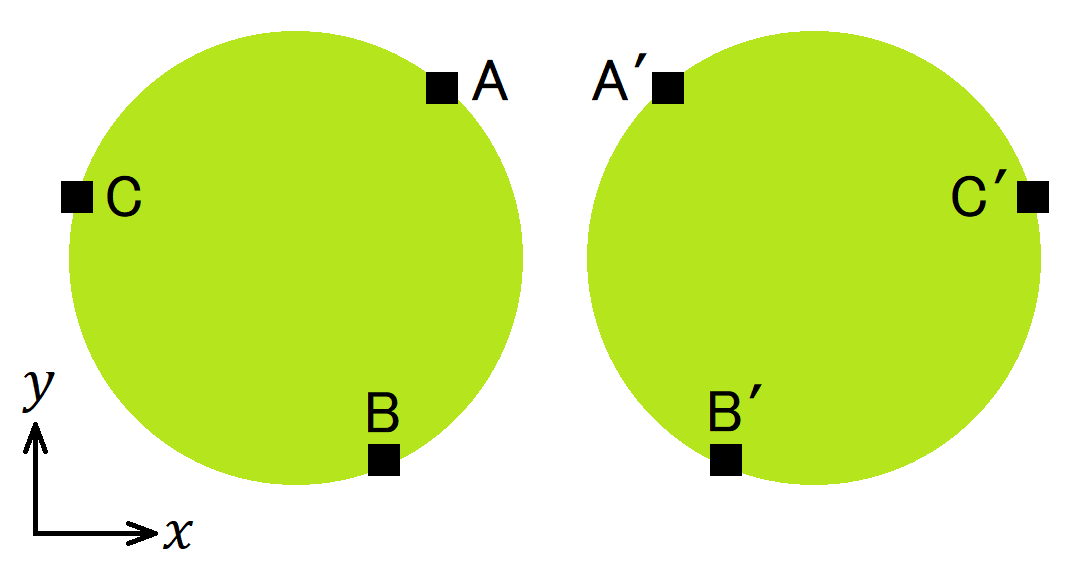
2次元世界の人間にとって、2次元平面が世界のすべてである。図2のように、今その2次元平面の中に2つの円板があり、それらはいくらでも自由に伸び縮みができるものとする。ここで2つの円板の端どうしを貼り合わせることとし、その際にAとA′、BとB′、CとC′がそれぞれ重なるようにする。そんなことを言われても2次元平面内ではどうがんばってもそのように貼り合わせる操作は不可能である。しかし2次元平面の外に出てもよければ簡単だ。3次元空間内で一方の円板をひっくり返して他方の円板に重ねればよい。こうして2つの円板の端をくっつけてできた多様体は端がない有限な2次元空間(曲面)である。そしてこれの真ん中を膨らませれば2次元球面ができあがる。2次元世界の人間はこのような話を聞いて実感はわかないけれども「2次元球面とはそういうものか。」と納得するしかない。
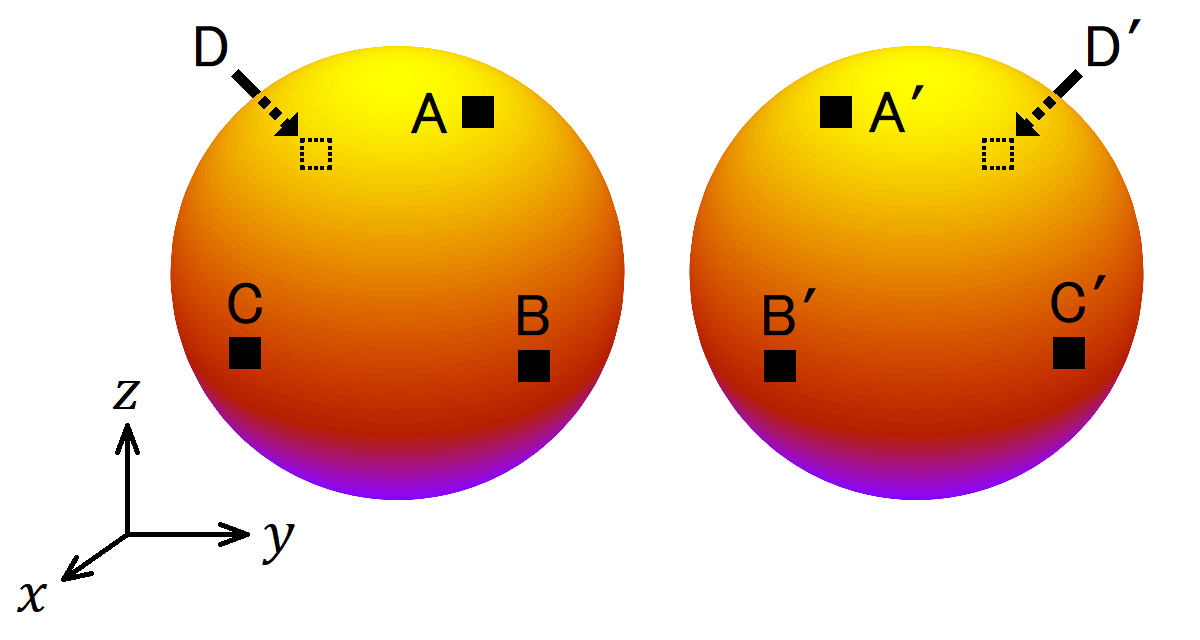
3次元超球面もこれと同じである。図3のように3次元空間内に2つの球体があり、それらはいくらでも自由に伸び縮みができるものとする。ここで2つの球体の表面同士を貼り合わせることとし、その際にAとA′、BとB′、CとC′、DとD′がそれぞれ重なるようにする。3次元空間内ではそんなことはできないがそこを飛び出して4次元空間に出れば可能である。実際に貼り合わせた状況は想像できないかもしれないが、2つの球体のAとA′、BとB′等がつながっているような空間を考えればよい。このようにして考えた2つの球体内部を合わせた空間は、端がない有限な3次元空間である。それを4次元空間内でちょうどよく伸縮させて形を整えれば3次元超球面になる。このように考えれば3次元超球面をイメージすることができるだろう。なお、(10)式の座標系では空間の半分しかカバーできないのであったが、その半分とは2つの球体の一方のことだと思えばよい。
1.3 一様・等方な時空の計量
ここまでは空間だけを考えてきた。ここからは時間についても考えていく。
座標系
座標系は次のように仮定する。
- 𝑥⁰ = 𝑤
- 時間座標(未来方向が正)
- 𝑥¹ = 𝑟
- 動径座標
- 𝑥² = 𝜃
- 角度座標(緯度:北極が0)
- 𝑥³ = 𝜑
- 角度座標(経度)
4次元時空の計量
一様・等方な3次元空間部分は(10)式を流用し、そこに時間を追加すれば4次元時空になる。空間的に一様であるから、どこの場所でも時間の流れ方は同じなので 𝑔₀₀ = −1 とする。これは空間の各点で静止している人にとっての固有時が座標時に等しいということである。また、3次元空間部分は一様であるが、その形を保ちながら時間にしたがって全体的に拡大や縮小することは構わないから、ある時刻を基準として、時刻 𝑤 における空間の大きさが基準時の 𝑎(𝑤) 倍だったとする。このような時空の線素の式は のようになる。 𝑎(𝑤) は 𝑤 の関数であり、その具体的な形は今のことろ未定である。この 𝑎(𝑤) をスケール因子(scale factor)と呼ぶ。ここではスケール因子は原則として正であるが宇宙の始まりと終わりの瞬間だけは0になってもよいこととしておく。
(11)式が一様・等方な時空の一般的な形であり、この計量を「フリードマン・ルメートル・ロバートソン・ウォーカー計量」(Friedmann–Lemaître–Robertson–Walker metric; FLRW計量)と呼ぶ。
静止する自由粒子
話が横道にそれるが、FLRW計量で表される時空では、スケール因子 𝑎(𝑤) の形にかかわらず、この座標系に対して静止している粒子の世界線は測地線である。すなわち、ある瞬間に静止している自由粒子はずっと静止し続けるということだ。空間は一様・等方なのだから、最初に静止していれば勝手に特定の方向に動き出すはずがないので、まあ当たり前であるような気はする。それに計量を見ると 𝑔₀₀ が定数であることからも重力ポテンシャルが一定である(から重力がゼロである)ことが予想できる。しかしきちんと測地線方程式を使ってこのことを確認しておこう。今からやる計算の結果は後で別のところもで使うので無駄にはならない。
測地線方程式にはクリストッフェル記号がいるので、それを求める。ここからは 𝑎 の引数を表す (𝑤) は省略することにする。まず計量テンソル 𝑔𝜇𝜈 は である。添え字が上にある 𝑔𝜇𝜈 は 𝑔𝜇𝜈 の逆行列であるが、今は対角行列であるから対角成分を逆数にするだけでよいので である。 𝑔𝜇𝜈 の微分のうち0でない成分は である。ただしドット ˙ は座標 𝑤 による微分 を表す。これら以外の成分はすべて0である。
クリストッフェル記号の定義は一般に である。だが、「シュバルツシルト解(外部解)の導出」の記事の「計量が対角行列のときに限って使えるクリストッフェル記号の公式」のところに書いたように、計量が対角行列のときに限りクリストッフェル記号の公式は3つの添え字のパターンに応じて次のように簡略化される。以下①〜④の欄に限り、アインシュタインの縮約記法を使っておらず、同じ添え字が2回現れても和を取ってはならない。
① 3つの添え字がすべて等しい成分
② 上付添え字のみが異なり、2つの下付添え字が等しい成分
③ 一方の下付添え字のみが異なり、他方の下付添え字と上付添え字が等しい成分
④ 3つの添え字がすべて異なる成分
ではクリストッフェル記号の各成分を求めよう。(13)〜(20)式を(21)〜(24)式の公式に代入する。
①のパターンは、 が0でないのは(17)式の 𝜆 = 1 の場合だけであるから、 であり、これ以外の場合は0である。②のパターンは、 が0でないのは(14)〜(16)・(18)〜(20)式の場合であるから、 であり、これら以外の場合は0である。③のパターンは、 が0でないのは(14)〜(16)・(18)〜(20)式の場合であるから、 であり、これら以外の場合は0である。④のパターンはすべて0である。以上でクリストッフェル記号のすべての成分が求まった。まとめてもう一度書いておくと、0でない成分は以下である。
さて、測地線方程式は である。ただしパラメータとして固有時 𝜏 を採用した。左辺第2項のクリストッフェル記号のところには(25)式を代入すればよい。
それで今やりたいことは、静止している粒子の世界線が測地線であることの確認であった。静止しているということは である。このことと、4元速度はいつでも を満たしていることと、 𝑔₀₀ = −1 から、 であることがわかる(𝑐 は光速)。したがって(26)式の左辺第1項は定数(0 または 𝑐)を微分したものになるのでいつでも0である。また、左辺第2項の の部分が0でない値になるのは 𝜇 = 𝜈 = 0 となる成分だけであるが、 𝛤𝜆₀₀ は 𝜆 にかかわらず(25)式に含まれていないので0であるから、第2項全体は0である。以上により、静止している粒子の世界線については常に(26)式が成り立つのでそれは測地線であることがわかる。