第3章 解の分類
ライスナー・ノルドシュトルム解の線素の式を改めて書くと、 である。 𝑘 を含む項がシュバルツシルト解からのずれを表している。 𝑟 が大きいところでずれは小さく、 𝑟 = 0 の近傍でずれが大きくなる。この解は物体の外部でしか成り立たないから、帯電した普通の物体が中心にあるときは 𝑟 = 0 の近傍のことは考えなくてよいが、ブラックホールの場合は解の適用範囲が 𝑟 → 0 まで広がる。
𝑟𝑠 と 𝑘 との関係に応じて解の性質は次のように変わる。
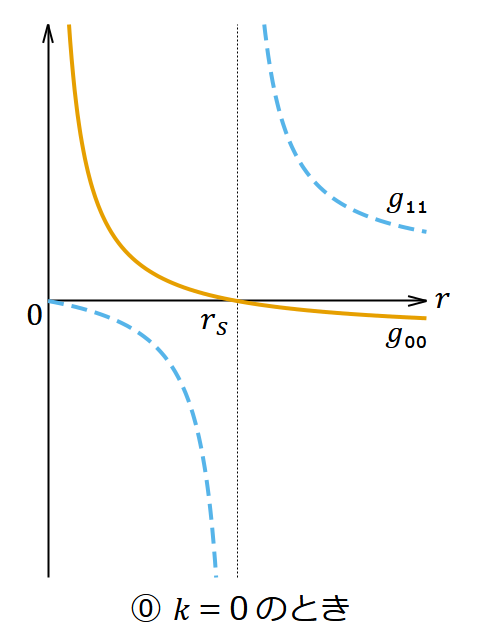
- ⓪ 𝑘 = 0 のとき
- シュバルツシルト解(外部解)そのものである。
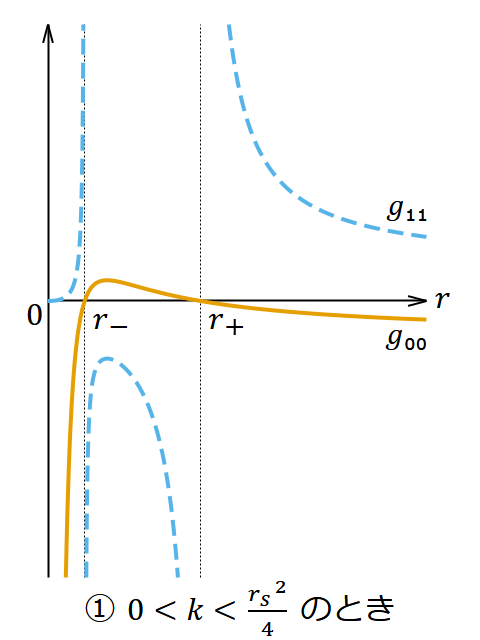
- ① のとき
- の2か所に地平面ができる。これらは座標特異点であり、うまく座標変換することで特異性は除去できる。 𝑟 = 𝑟+ (< 𝑟𝑠) がブラックホールの表面である。 𝑟− < 𝑟 < 𝑟+ の領域では 𝑤 座標が空間的、 𝑟 座標が時間的になっている。 0 < 𝑟 < 𝑟− の領域まで行くと再び 𝑤 座標が時間的、 𝑟 座標が空間的になる。そこでは時間は 𝑤 の正負どちら向きに流れているのかって? それはまた別の機会に考えよう。
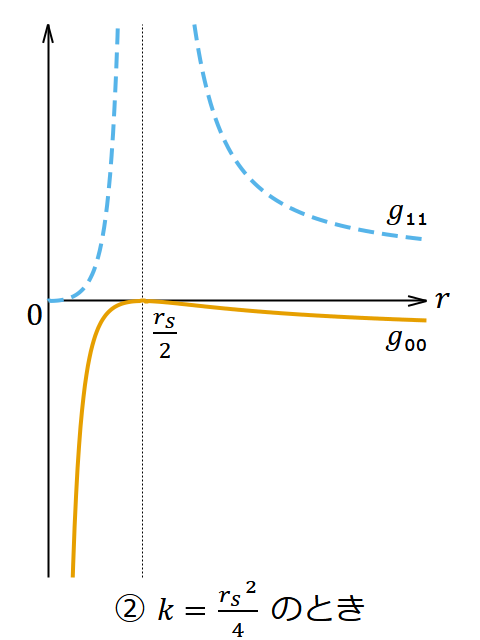
- ② のとき
- 𝑟+ と 𝑟− が一致し、 に事象の地平面ができる。
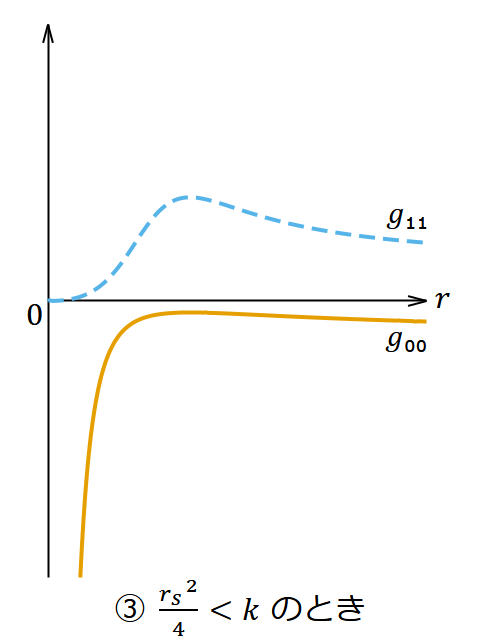
- ③ のとき
- 事象の地平面はない。
それぞれの場合の 𝑔₀₀ と 𝑔₁₁ の挙動は図1のようになる。どの場合でも 𝑟 = 0 は真の特異点である。③は特異点が事象の地平面に囲まれておらずむき出しになっていて一大事である。
ちょうど②になるときの電荷と質量の関係を計算してみると、 になっていることがわかる。(52)式の両辺は、電荷が 𝑄 で質量が 𝑀 の同じ物体を2つ持ってきて1m離して置いたときに両物体の間に働く電磁気力(斥力)と重力(引力)の大きさを、非相対論的に計算したものと同じである。それが等号でつながっているので、2つの力が釣り合うということだ(1m離して釣り合うなら何m離しても釣り合う)。もし左辺の方が小さければ①になるし大きければ③になる。地平面の有無を分ける条件と、静電力と重力が釣り合う(非相対論的な)条件が、なぜ一致するのかは知らない。偶然なのだろうか。
解の性質について話すと長くなりそうである。解の導出はもうできたので、当記事はここまでにしておこう。