「双子のパラドックス」を両者の視点から計算する。(1)

相対性理論におけるいわゆる「双子のパラドックス」とは、次のようなものだ。

これは単に相対性理論を勘違いしているだけのことであり、パラドックスではない。相対性理論に従って計算すれば、どのような視点（座標系）で計算しようとも、アリスが多く歳を取るという一貫した結果が導き出される。では上の話のどこがおかしいかといえば、「運動する物体の時間は遅れる」の法則は慣性系で測ったときにしか成り立たないので、途中で（少なくとも折り返しのときに）加速度運動するボブの視点から見たときにはその法則は使えないのである。ただそれだけだ。「どこがおかしいか」を言うだけなら、これ以上の説明は不要であるし、余計な説明をするとかえって混乱する。

上記がパラドックスでないことはよいとして、それなら加減速時も含めて正しくはどう計算されるのか。これを両者の視点から定量的に計算した説明はあまり見かけない。たぶん、めんどくさい割に学術的には大して重要でないからであろう。しかし具体的にどう計算されるのか気になる人もいると思うので、ここでは特殊相対性理論および一般相対性理論の手法を用いて実際にアリスの視点とボブの視点の両方で定量的に計算して、それらの結果が一致しパラドックスがないことを示す。

念のために言っておくが、ここでやることは相対性理論に上記のような自己矛盾がなく一貫していることを示すだけであり、これをもって相対性理論が正しいことが証明されるわけではない。相対性理論が正しいかどうかは、実験して観測した値と相対性理論に基づいた予測値とを比較して初めてわかることである。それはまた別の話題なのでここでは触れない。

最初に計算結果

せっかちな人のために、まず答えを書いておく。求め方は後で説明する。

ボブが帰ってきたとき、ボブの経過時間は定義により 4𝑇₁ + 2𝑇₂ である。一方、アリスの経過時間を計算すると $2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ になり、これは 4𝑇₁ + 2𝑇₂ より大きい。これはボブの視点の座標系で計算しようがアリスの視点の座標系で計算しようが同じである。ここで 𝑐 は光速である。 $\sinh$ や $\cosh$ は普通の数学に（相対性理論と関係なく）出てくる双曲線関数と呼ばれるものであり、その定義は $\sinh 𝑥 = \frac{e^{𝑥} - e^{- 𝑥}}{2}$ 、 $\cosh 𝑥 = \frac{e^{𝑥} + e^{- 𝑥}}{2}$ である。 $\tanh 𝑥 = \frac{\sinh 𝑥}{\cosh 𝑥} = \frac{e^{𝑥} - e^{- 𝑥}}{e^{𝑥} + e^{- 𝑥}}$ というのもある。双曲線関数についてもっと詳しいことはよそで勉強してきてほしい。

途中経過も含めたアリスの時間とボブの時間の対応の例は表1のようになる。

表1. アリスにとっての同時刻のボブと、ボブにとっての同時刻のアリスの、対応の例
アリスに固定した座標系の例（ミンコフスキー座標）		ボブのできごと	ボブに固定した座標系の例（ミンコフスキー座標とリンドラー座標を切り貼りした座標）
座標時（=アリスの経過時間）	ボブの経過時間	ボブのできごと	座標時（=ボブの経過時間）	アリスの経過時間
$0$	$0$	出発	$0$	$0$
$\frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$𝑇₁$	往路加速終了	$𝑇₁$	$\frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐}$
$𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$𝑇₁ + 𝑇₂$	往路減速開始	$𝑇₁ + 𝑇₂$	$\frac{𝑇₂}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐}$
$𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{2 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$2 𝑇₁ + 𝑇₂$	折り返し	$2 𝑇₁ + 𝑇₂$	$𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{2 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$
$𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{3 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$3 𝑇₁ + 𝑇₂$	復路加速終了	$3 𝑇₁ + 𝑇₂$	$𝑇₂ \sinh \frac{𝑎 𝑇₁}{𝑐} \tanh \frac{𝑎 𝑇₁}{𝑐} + 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$
$2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{3 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$3 𝑇₁ + 2 𝑇₂$	復路減速開始	$3 𝑇₁ + 2 𝑇₂$	$2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$
$2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$	$4 𝑇₁ + 2 𝑇₂$	帰還	$4 𝑇₁ + 2 𝑇₂$	$2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$

「例」と言った理由は、離れた場所における「同時」を一意に決定するような基準はないので、これが唯一の正解ではないからである。一般的に、離れた場所における「同時」とは、「その座標系において時間座標の値（座標時）が同じである事象」といった程度の人為的な意味しかない。物理的に普遍的な意味はないのだ。どのような座標系を使うかは人間の自由であり人間が責任を持って決める必要がある。表1で採用した座標系は対称性が高く計算がやりやすいように選んだものである。

ただし同一の場所における同時は一意に決まる。アリスとボブが同一の場所にいるとき、例えば45歳のアリスにとっての現在のボブが36歳だとしたら、その36歳のボブにとっての現在のアリスは45歳である。同一の場所でこれが食い違うことはあり得ない。

一つ注意してほしいのは、例えばアリスが望遠鏡でボブを観察したとして、現在のアリスにとっての同時刻のボブが見えるわけではないということである。光の速度は有限であるから、見えているのは過去のボブである。「アリスがいつの時点のボブを見るか」を知りたければ、表1の値に対して光の伝搬時間を加味して時間差を補正する必要がある。ボブから見たアリスについても同様である。（当たり前だが、この「いつの時点の相手が見えるか」は座標系に関係なく一意に決まる。）

下の2つの図はそれぞれアリスとボブに固定した座標系で両者の世界線を表したものである。2つの図の縮尺は同じである。水色の線はアリスの世界線、茶色の線はボブの世界線を表す。𝜏_𝐴 はアリスの固有時、𝜏_𝐵 はボブの固有時である。

表1および上図では、出発時の時刻を基準として、ボブが帰還するときまでの経過時間を2つの座標系で計算してある。アリスとボブが離れた場所にいるときは「同時」の見解が互いに異なっているが、帰還時における両者の経過時間のずれはどちらの座標系で計算しても同じであることを表している。

ではこれから具体的に表1の値を導出する手順を説明する。

A. アリスの視点から見た座標系

この章では表1の左半分すなわちアリスに固定した座標系での計算を行う。まずどのような座標系を使うかを決めるのであるが、アリスは慣性系で静止しているのだから、ここは素直に普通のミンコフスキー座標を使って特殊相対性理論で計算すればよい。家の位置を 𝑥 = 0, 𝑦 = 0, 𝑧 = 0 として、ボブが出発する時刻を 𝑡 = 0 とするのである。また、ボブが移動する空間的方向を𝑥軸にとる。

座標系が決まったら、この座標系でボブの世界線を表す方程式を求める。

A.1. 出発局面

ボブの運動は一様ではないので、その局面ごとに別々に求める必要がある。まず出発し加速開始してから加速をやめるまでの間（これを「出発局面」とする。）の運動を求める。求め方は単純で、「4元速度を固有時で微分したもの」と「4元加速度」とが等しいという微分方程式を解くのである。その準備として、4元速度と4元加速度と固有時を未知関数で表すことから始める。

アリスの座標系で測った時刻 𝑡 におけるボブの速度（普通の3次元的な速度）の𝑥成分を未知関数 𝑣(𝑡) と置く。𝑦成分と𝑧成分は0である。するとアリスの座標系で測った時刻 𝑡 におけるボブの4元速度 $𝑢^{𝜇} (𝑡)$ は定義により $(\begin{matrix} 𝑢^{0} (𝑡) \\ 𝑢^{1} (𝑡) \\ 𝑢^{2} (𝑡) \\ 𝑢^{3} (𝑡) \end{matrix}) = (\begin{matrix} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ 0 \\ 0 \end{matrix}) (1)$ である。ここで添え字の0は𝑐𝑡成分、1は𝑥成分、2は𝑦成分、3は𝑧成分をそれぞれ表す。この $𝑢^{𝜇} (𝑡)$ を𝑐で割ったものを4元速度と定義する流儀もあるので、気を付けてほしい。

ボブの加速度は𝑥方向に一定の 𝑎 であり、4元加速度は (0, 𝑎, 0, 0) である。これは瞬間的にボブと同じ速度で動いている慣性系で測った値である。ここはちょっとわかりにくい。ボブの座標系でボブの加速度を測ったら、ボブはずっと空間原点にいるのだから加速度は0ではないか、と思うだろう。そのとおりである。しかしここで言っているのは一定速度 𝑣(𝑡) で運動する慣性系であって、それは時刻 𝑡 の瞬間にだけ速度がボブと一致する。つまりその慣性系から見るとボブの速度が0になるのはその一瞬だけである。それから（アリスの座標系で測って）無限小時間 d𝑡 が経過したのちはボブの速度は（アリスの座標系で測って） 𝑣(𝑡+d𝑡) になっており、このとき一定速度 𝑣(𝑡) で運動する慣性系で測ったボブの速度はもはや0ではない。時間当たりのその変化分が加速度 𝑎 である。

したがって、その4元加速度に対して速度 −𝑣(𝑡) に対応するローレンツ変換を施せばアリスの座標系での値になる。ローレンツ変換の場合は位置ベクトルの変換もそうでない4元ベクトルの反変成分の変換も変換式は同じである（一般の座標変換ではそうはいかない）。よって、アリスの座標系で測った時刻 𝑡 におけるボブの4元加速度 $𝛼^{𝜇} (𝑡)$ は $(\begin{matrix} 𝛼^{0} (𝑡) \\ 𝛼^{1} (𝑡) \\ 𝛼^{2} (𝑡) \\ 𝛼^{3} (𝑡) \end{matrix}) = (\begin{matrix} \frac{1}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & \frac{\frac{𝑣 (𝑡)}{𝑐}}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & 0 & 0 \\ \frac{\frac{𝑣 (𝑡)}{𝑐}}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & \frac{1}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) (\begin{matrix} 0 \\ 𝑎 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} \frac{\frac{𝑣 (𝑡)}{𝑐} 𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ 0 \\ 0 \end{matrix}) (2)$ である。ところで今 𝑎 は正という設定であるが、この先の微分方程式を解くまでの式変形は 𝑎 の符号に依存しないことを意識してもらいたい。理由は、しばらくあとで 𝑎 に負の値を入れた式を使う予定だからだ。ただし 𝑎 は0ではないとする。

次に、ボブの固有時を 𝜏_𝐵 とすると $\frac{{d𝜏}_{𝐵}}{d𝑡} = \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} (3)$ である。(3)式はミンコフスキー座標において公式のようなものだが、忘れてしまったときは線素の式からスタートして次のように導けばよい。

\begin{array}{l} - {(𝑐 {d𝜏}_{𝐵})}^{2} & = & - {(𝑐 d𝑡)}^{2} + {d𝑥}^{2} + {d𝑦}^{2} + {d𝑧}^{2} \\ {(\frac{{d𝜏}_{𝐵}}{d𝑡})}^{2} & = & 1 - \frac{1}{𝑐^{2}} {{(\frac{d𝑥}{d𝑡})}^{2} + {(\frac{d𝑦}{d𝑡})}^{2} + {(\frac{d𝑧}{d𝑡})}^{2}} & ←両辺を−(𝑐d𝑡)²で割った。 \\ {(\frac{{d𝜏}_{𝐵}}{d𝑡})}^{2} & = & 1 - \frac{{𝑣 (𝑡)}^{2}}{𝑐^{2}} & ←三平方の定理。 \\ \frac{{d𝜏}_{𝐵}}{d𝑡} & = & \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} & ← 𝑡 が増えるとき 𝜏_{𝐵} も増えてほしいので正の平方根を採用。 \end{array}

この 𝜏_𝐵 を𝑐倍したものを固有時と定義する流儀もあるので、気を付けてほしい。

これで準備は整った。今から解くべき、「4元速度を固有時で微分したもの」と「4元加速度」とが等しいという微分方程式は $\frac{{d𝑢}^{𝜇} (𝑡)}{{d𝜏}_{𝐵}} = 𝛼^{𝜇} (𝑡) (4)$ である。添え字の 𝜇 には 0, 1, 2, 3 が入るのでこれは4個の式からなる連立方程式であるが、今は第2・3成分（𝑦, 𝑧成分）は 0 = 0 という恒等式になる。この後も第2・3成分はずっと0なのでこの章ではこれ以上書かない。第0・1成分については、(1)・(2)式で準備した $𝑢^{0} (𝑡)$ , $𝛼^{0} (𝑡)$ , $𝑢^{1} (𝑡)$ , $𝛼^{1} (𝑡)$ の具体的な表式を第0・1成分の方程式に代入すると、 $\begin{matrix} 第0成分 & \frac{d}{{d𝜏}_{𝐵}} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} = \frac{\frac{𝑣 (𝑡)}{𝑐} 𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & (5) \\ 第1成分 & \frac{d}{{d𝜏}_{𝐵}} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} = \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & (6) \end{matrix}$ のようになる。未知関数が1個しかないのに式が2個もあって、解が存在するのか不安になるかもしれないが、そこはうまくできているので心配はいらない。後で具体的に確認する。

これを解くには第1成分である(6)式を使う。

\begin{array}{l} \frac{d}{{d𝜏}_{𝐵}} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & ← (6)式 \\ \frac{d𝑡}{{d𝜏}_{𝐵}} \frac{d}{d𝑡} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ \frac{1}{(\frac{{d𝜏}_{𝐵}}{d𝑡})} \frac{d}{d𝑡} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ \frac{1}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \frac{d}{d𝑡} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & \frac{𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & ← (3)式 を代入した。 \\ \frac{d}{d𝑡} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & 𝑎 \\ \int \frac{d}{d𝑡} \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} d𝑡 & = & \int 𝑎 d𝑡 \\ \frac{𝑣 (𝑡)}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & = & 𝑎 𝑡 + 𝐾₀ & （𝐾₀は積分定数） \end{array}

ここで初期条件 𝑡 = 0 のとき 𝑣(0) = 0 より積分定数は 𝐾₀ = 0 と決めることができるが、あとで一般解を使いたいので 𝐾₀ のまま式変形を続ける。

\begin{array}{l} 𝑣 (𝑡) & = & (𝑎 𝑡 + 𝐾₀) \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} \\ {𝑣 (𝑡)}^{2} & = & {(𝑎 𝑡 + 𝐾₀)}^{2} {1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} \\ {𝑣 (𝑡)}^{2} & = & {(𝑎 𝑡 + 𝐾₀)}^{2} - {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2} {𝑣 (𝑡)}^{2} \\ {1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} {𝑣 (𝑡)}^{2} & = & {(𝑎 𝑡 + 𝐾₀)}^{2} \\ {𝑣 (𝑡)}^{2} & = & \frac{{(𝑎 𝑡 + 𝐾₀)}^{2}}{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} & (7) \\ 𝑣 (𝑡) & = & \pm \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} \end{array}

6行上を見ると 𝑣(𝑡) と 𝑎𝑡+𝐾₀ が同符号であることがわかるので、複号は正を採用し、 $𝑣 (𝑡) = \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} (8)$ が一般解である。

ここで $\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}$ という量がこの後何度も出てくるので先に計算しておく。

\begin{array}{l} \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} & = & \sqrt{1 - \frac{1}{𝑐^{2}} {𝑣 (𝑡)}^{2}} \\ = & \sqrt{1 - \frac{1}{𝑐^{2}} \frac{{(𝑎 𝑡 + 𝐾₀)}^{2}}{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} & ← (7)式 を代入した。 \\ = & \sqrt{1 - \frac{{(𝑎 𝑡 + 𝐾₀)}^{2}}{𝑐^{2} + {(𝑎 𝑡 + 𝐾₀)}^{2}}} \\ = & \sqrt{\frac{𝑐^{2}}{𝑐^{2} + {(𝑎 𝑡 + 𝐾₀)}^{2}}} \\ = & \frac{1}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} & (9) \end{array}

ところで(8)式の 𝑣(𝑡) の導出には今のところ微分方程式(4)式のうち第1成分である(6)式しか使っていないのであった。これが第0成分である(5)式をも満たしているかどうかを確認しよう。

\begin{array}{l} (5)式の左辺 & = & \frac{d}{{d𝜏}_{𝐵}} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ = & \frac{d𝑡}{{d𝜏}_{𝐵}} \frac{d}{d𝑡} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ = & \frac{1}{(\frac{{d𝜏}_{𝐵}}{d𝑡})} \frac{d}{d𝑡} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ = & \frac{1}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \frac{d}{d𝑡} \frac{𝑐}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} & ← (3)式 を代入した。 \\ = & \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} \frac{d}{d𝑡} {𝑐 \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} & ← (9)式 を代入した。 \\ = & \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} 𝑐 \frac{1}{2 \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} 2 (\frac{𝑎 𝑡 + 𝐾₀}{𝑐}) \frac{𝑎}{𝑐} \\ = & \frac{𝑎 (𝑎 𝑡 + 𝐾₀)}{𝑐} \\ (5)式の右辺 & = & \frac{\frac{𝑣 (𝑡)}{𝑐} 𝑎}{\sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}}} \\ = & \frac{1}{𝑐} \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} 𝑎 \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} & ← (8) ・ (9)式 を代入した。 \\ = & \frac{𝑎 (𝑎 𝑡 + 𝐾₀)}{𝑐} \end{array}

以上より、左辺と右辺が等しいので確かに(5)式も成り立っている。

次にボブの固有時を求める。(3)式より、 $\begin{array}{l} \frac{{d𝜏}_{𝐵}}{d𝑡} & = & \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} \\ = & \frac{1}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} & ← (9)式を代入した。 \\ 𝜏_{𝐵} & = & \int \frac{1}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} d𝑡 \\ = & \frac{𝑐}{𝑎} arsinh \frac{𝑎 𝑡 + 𝐾₀}{𝑐} + 𝐾₁ & （𝐾₁は積分定数） & (10) \end{array}$ となる。 $arsinh$ は $\sinh$ の逆関数である。最後の等号は微分の公式 $\frac{d}{d𝑥} arsinh 𝑥 = \frac{1}{\sqrt{1 + 𝑥^{2}}}$ を使った。(10)式を 𝑡 について解く。

\begin{array}{l} \frac{𝑐}{𝑎} arsinh \frac{𝑎 𝑡 + 𝐾₀}{𝑐} + 𝐾₁ & = & 𝜏_{𝐵} \\ \frac{𝑐}{𝑎} arsinh \frac{𝑎 𝑡 + 𝐾₀}{𝑐} & = & 𝜏_{𝐵} - 𝐾₁ \\ arsinh \frac{𝑎 𝑡 + 𝐾₀}{𝑐} & = & \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} \\ \frac{𝑎 𝑡 + 𝐾₀}{𝑐} & = & \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} & (11) \\ 𝑎 𝑡 + 𝐾₀ & = & 𝑐 \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} & (12) \\ 𝑎 𝑡 & = & 𝑐 \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} - 𝐾₀ \\ 𝑡 & = & \frac{𝑐}{𝑎} \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} - \frac{𝐾₀}{𝑎} & (13) \end{array}

これで座標時とボブの固有時とボブの速度（普通の3次元的な速度）の関係が明らかになった。せっかくだから速度を積分して、アリスの座標系で測った時刻 𝑡 におけるボブの位置 𝑥(𝑡) も求めておこう。

\begin{array}{l} 𝑥 (𝑡) & = & \int 𝑣 (𝑡) d𝑡 \\ = & \int \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} d𝑡 \\ = & \frac{𝑐^{2}}{𝑎} \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} + 𝐾₂ & （𝐾₂は積分定数） (14) \end{array}

また、 𝑣(𝑡) と 𝑥(𝑡) をそれぞれ 𝜏_𝐵 でパラメータ表示したものを求めると、(8)式より $\begin{array}{l} 𝑣 (𝑡) & = & \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}} \\ = & \frac{𝑐 \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}}{\sqrt{1 + \sinh^{2} \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}}} & ← (12) ・ (11)式を代入した。 \\ = & \frac{𝑐 \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}}{\sqrt{\cosh^{2} \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}}} \\ = & \frac{𝑐 \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}}{\cosh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}} \\ = & 𝑐 \tanh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} & (15) \end{array}$ であり、(14)式より $\begin{array}{l} 𝑥 (𝑡) & = & \frac{𝑐^{2}}{𝑎} \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} + 𝐾₂ \\ = & \frac{𝑐^{2}}{𝑎} \sqrt{1 + \sinh^{2} \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}} + 𝐾₂ & ← (11)式を代入した。 \\ = & \frac{𝑐^{2}}{𝑎} \sqrt{\cosh^{2} \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}} + 𝐾₂ \\ = & \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} + 𝐾₂ & (16) \end{array}$ となる。

以上でボブの固有時と速度と位置の一般解が求まった。(13)・(10)・(8)・(15)・(14)・(16)式で得られた一般解を表2にまとめておく。

表2. 微分方程式(3)・(4)式の一般解
	座標時 𝑡 による表示		ボブの固有時 𝜏_𝐵 によるパラメータ表示
座標時		𝑡	(13)	$\frac{𝑐}{𝑎} \sinh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} - \frac{𝐾₀}{𝑎}$
ボブの固有時	(10)	$\frac{𝑐}{𝑎} arsinh \frac{𝑎 𝑡 + 𝐾₀}{𝑐} + 𝐾₁$		𝜏_𝐵
ボブの速度	(8)	$𝑣 (𝑡) = \frac{𝑎 𝑡 + 𝐾₀}{\sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}}}$	(15)	$𝑐 \tanh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐}$
ボブの位置	(14)	$𝑥 (𝑡) = \frac{𝑐^{2}}{𝑎} \sqrt{1 + {(\frac{𝑎 𝑡 + 𝐾₀}{𝑐})}^{2}} + 𝐾₂$	(16)	$\frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 (𝜏_{𝐵} - 𝐾₁)}{𝑐} + 𝐾₂$
	（𝐾₀, 𝐾₁, 𝐾₂ は積分定数）

表2の右の列は、アリスの座標系で計算したボブの世界線の座標 (𝑡, 𝑥) をボブの固有時 𝜏_𝐵 によってパラメータ表示したものである。ボブの座標系で計算したものではない。ボブの座標系で計算する作業は第B章で行う。

最初のほうで述べたように、この一般解は 𝑎 が0のときは使えないが0でなければ正でも負でも成り立つ。そして初期条件として例えば特定の時刻におけるボブの固有時と位置と速度を与えれば、積分定数 𝐾₀, 𝐾₁, 𝐾₂ が定まるわけである。

では具体的に出発局面の特殊解を求めよう。出発局面における初期条件は、時刻（座標時） 𝑡 = 0 のときボブの位置は 𝑥(0) = 0 、ボブの速度は 𝑣(0) = 0 であり、またボブの固有時も出発時を基準にしたいので 𝑡 = 0 のとき 𝜏_𝐵 = 0 とする。これらを表2の一般解に代入すれば、簡単な計算により積分定数は $𝐾₀ = 0$ , $𝐾₁ = 0$ , $𝐾₂ = - \frac{𝑐^{2}}{𝑎}$ のように定まるので、特殊解は表3のようになる。

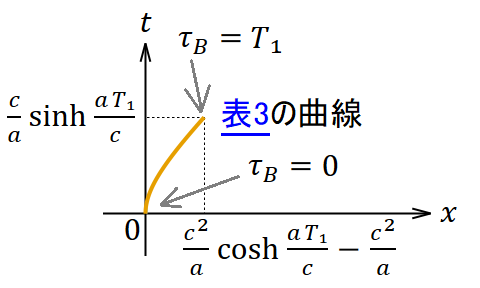
表3. 出発局面 (0 ≦ 𝜏_𝐵 ≦ 𝑇₁) における微分方程式(3)・(4)式の特殊解
	座標時 𝑡 による表示	ボブの固有時 𝜏_𝐵 によるパラメータ表示
座標時	𝑡	$\frac{𝑐}{𝑎} \sinh \frac{𝑎 𝜏_{𝐵}}{𝑐}$
ボブの固有時	$\frac{𝑐}{𝑎} arsinh \frac{𝑎 𝑡}{𝑐}$	𝜏_𝐵
ボブの速度	$𝑣 (𝑡) = \frac{𝑎 𝑡}{\sqrt{1 + {(\frac{𝑎 𝑡}{𝑐})}^{2}}}$	$𝑐 \tanh \frac{𝑎 𝜏_{𝐵}}{𝑐}$
ボブの位置	$𝑥 (𝑡) = \frac{𝑐^{2}}{𝑎} \sqrt{1 + {(\frac{𝑎 𝑡}{𝑐})}^{2}} - \frac{𝑐^{2}}{𝑎}$	$\frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝜏_{𝐵}}{𝑐} - \frac{𝑐^{2}}{𝑎}$

出発局面の終了時では、 𝜏_𝐵 = 𝑇₁ であるからこれを表3の特殊解に代入すると、座標時は $\frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの速度は $𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの位置は $\frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎}$ である。

A.2. 往路惰行局面

次に往路の加速をやめてから減速を始めるまでの、加速度が0である期間（これを「往路惰行局面」とする。）を考える。

この局面の開始時は出発局面の終了時と同じであるから、ボブの固有時は定義により 𝑇₁ であり、A.1節の最後で計算したようにそのときの座標時は $\frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの速度は $𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの位置は $\frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎}$ である。これが初期条件となる。

往路惰行局面を通して加速度が0であるから、速度 $𝑣 (𝑡) = 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$ は一定である。したがって固有時 𝜏_𝐵 は(3)式より $\begin{array}{l} \frac{{d𝜏}_{𝐵}}{d𝑡} & = & \sqrt{1 - {(\frac{𝑣 (𝑡)}{𝑐})}^{2}} \\ = & \sqrt{1 - {(\frac{𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}}{𝑐})}^{2}} \\ = & \sqrt{1 - \tanh^{2} \frac{𝑎 𝑇₁}{𝑐}} \\ = & \sqrt{\frac{1}{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}} \\ = & \frac{1}{\cosh \frac{𝑎 𝑇₁}{𝑐}} \\ 𝜏_{𝐵} & = & \int \frac{1}{\cosh \frac{𝑎 𝑇₁}{𝑐}} d𝑡 \\ = & \frac{𝑡}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝐾₃ & （𝐾₃は積分定数） & (17) \end{array}$ となる。初期条件は $𝑡 = \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ のとき 𝜏_𝐵 = 𝑇₁ であるからこれを(17)式に代入すると $\begin{array}{l} 𝑇₁ & = & \frac{\frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝐾₃ \\ 𝑇₁ & = & \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + 𝐾₃ \\ 𝑇₁ - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} & = & 𝐾₃ \end{array}$ のように積分定数 𝐾₃ が定まる。これを(17)式に代入すると固有時は $𝜏_{𝐵} = \frac{𝑡}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₁ - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} (18)$ となる。(18)式を 𝑡 について解くと $\begin{array}{l} \frac{𝑡}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₁ - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} & = & 𝜏_{𝐵} \\ \frac{𝑡}{\cosh \frac{𝑎 𝑇₁}{𝑐}} & = & 𝜏_{𝐵} - 𝑇₁ + \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} \\ 𝑡 & = & (𝜏_{𝐵} - 𝑇₁) \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} \cosh \frac{𝑎 𝑇₁}{𝑐} \\ = & (𝜏_{𝐵} - 𝑇₁) \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} & (19) \end{array}$ である。速度 𝑣(𝑡) が 𝑡 によらず一定であるから、位置 𝑥(𝑡) は座標時 𝑡 の1次関数になるので速度と初期条件の座標を使って $\begin{array}{l} 𝑥 (𝑡) & = & (𝑡 - 𝑡 の初期値) 𝑣 (𝑡) + 𝑥(𝑡) の初期値 \\ = & (𝑡 - \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎} & (20) \end{array}$ と表される。ついでに、(19)式を(20)式に代入して 𝑥(𝑡) を 𝜏_𝐵 で表してみる。

\begin{array}{l} 𝑥 (𝑡) & = & {(𝜏_{𝐵} - 𝑇₁) \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}} 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎} \\ = & {(𝜏_{𝐵} - 𝑇₁) \cosh \frac{𝑎 𝑇₁}{𝑐}} 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎} \\ = & 𝑐 (𝜏_{𝐵} - 𝑇₁) \sinh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎} & (21) \end{array}

(18)〜(21)式をまとめたものが表4だ。

表4. 往路惰行局面 (𝑇₁ ≦ 𝜏_𝐵 ≦ 𝑇₁+𝑇₂) における解
	座標時 𝑡 による表示		ボブの固有時 𝜏_𝐵 によるパラメータ表示
座標時		𝑡	(19)	$(𝜏_{𝐵} - 𝑇₁) \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$
ボブの固有時	(18)	$\frac{𝑡}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₁ - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐}$		𝜏_𝐵
ボブの速度（一定）		$𝑣 (𝑡) = 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$		$𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$
ボブの位置	(20)	$𝑥 (𝑡) = 𝑐 (𝑡 - \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎}$	(21)	$𝑐 (𝜏_{𝐵} - 𝑇₁) \sinh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎}$

往路惰行局面の終了時では、 𝜏_𝐵 = 𝑇₁+𝑇₂ であるからこれを表4の解に代入すると、座標時は $𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの速度は $𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}$ 、ボブの位置は $𝑐 𝑇₂ \sinh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎} \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐^{2}}{𝑎}$ である。

「双子のパラドックス」を両者の視点から計算する。(1)

目次

条件設定

最初に計算結果

A. アリスの視点から見た座標系

A.1. 出発局面

A.2. 往路惰行局面

「双子のパラドックス」を両者の視点から計算する。(1)

目次

条件設定

最初に計算結果

A. アリスの視点から見た座標系

A.1. 出発局面

A.2. 往路惰行局面

MathJax（数式表示用 JavaScript）使用設定

説明