座標変換

出発局面で採用するS₍₁₎系はどのような座標系であろうか。まずS₍₁₎系の縦軸がS₍₀₎系でどのように表されるべきかを考える。S₍₁₎系の縦軸とはつまり出発局面におけるボブの世界線のことである。S₍₀₎系は前章のアリスの立場のミンコフスキー座標と同じであるから、その座標系におけるボブの世界線はA.1節の表3で導出済みである。出発局面ではボブの固有時 𝜏_𝐵 はS₍₁₎系の座標時 ${𝑡}_{\mathrm{(1)}}$ と同じであるから先ほど定義した変数名を使って書き直すと、 $$\{\begin{array}{l}{𝑡}_{\mathrm{(0)}}=\frac{𝑐}{𝑎}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ {𝑥}_{\mathrm{(0)}}=\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\end{array}\text{(51)}$$ となる。しかし(51)式は ${\mathrm{𝑐𝑡}}_{\mathrm{(1)}}$ 軸上（${𝑥}_{\mathrm{(1)}}=0$）の場所専用の変換式であって、それ以外の場所では使えないのであまり役に立たない。

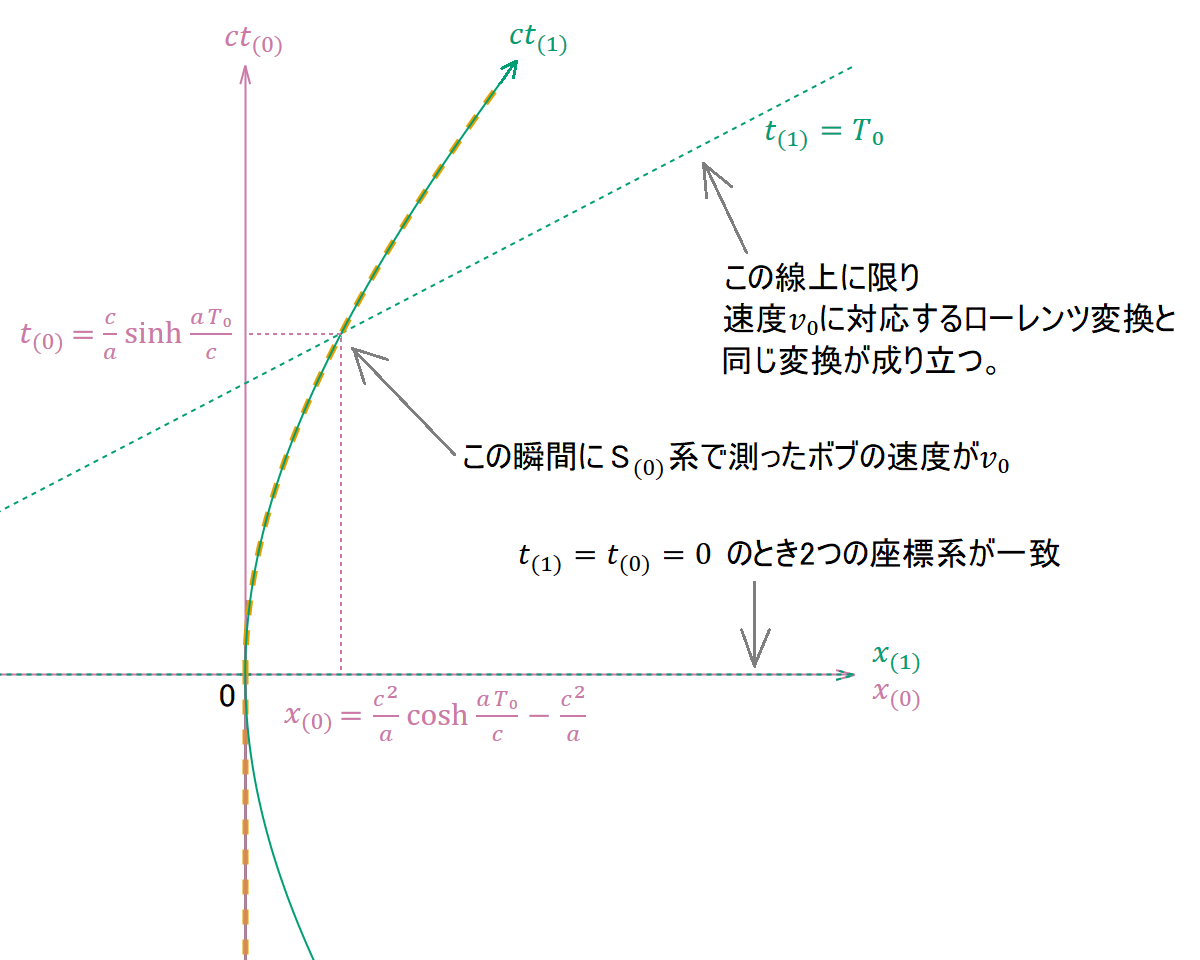
一般の場所でも使えるように、次のような安直な変換を考えてみる。S₍₀₎系から見てボブの速度は刻々と変わるが、ある瞬間だけを考えれば速度は一意に定まる。例えば ${𝑡}_{\mathrm{(1)}}=\mathrm{𝛵₀}\text{（定数）}$ のときのボブの速度を 𝑣₀ とすると、表3より $\mathrm{𝑣₀}=𝑐\tanh \frac{𝑎\mathrm{𝛵₀}}{𝑐}$ である。そこでその時点のボブから見て同時刻とみなせる事象、つまりS₍₁₎系において ${𝑥}_{\mathrm{(1)}}$ の値にかかわらず ${𝑡}_{\mathrm{(1)}}=\mathrm{𝛵₀}$ を満たす事象については、速度 𝑣₀ に対応するローレンツ変換と同じ変換でS₍₀₎系と結ばれていると仮定するのである。今、 $$\begin{array}{lll}\hfill \frac{\mathrm{𝑣₀}}{𝑐}& =& \frac{𝑐\tanh \frac{𝑎\mathrm{𝛵₀}}{𝑐}}{𝑐}\\ & =& \tanh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\\ \hfill \frac{1}{\sqrt{1-{\left(\frac{\mathrm{𝑣₀}}{𝑐}\right)}^2}}& =& \frac{1}{\sqrt{1-{\tanh }^2\frac{𝑎\mathrm{𝛵₀}}{𝑐}}}\\ & =& \frac{1}{\sqrt{\frac{1}{{\cosh }^2\frac{𝑎\mathrm{𝛵₀}}{𝑐}}}}\\ & =& \cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\end{array}$$ であるから、速度 −𝑣₀ に対応するローレンツ変換を考えると $$\begin{array}{lll}\left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(0)}}\\ {𝑥}_{\mathrm{(0)}}\end{array}\right)& =& \left(\begin{array}{cc}\frac{1}{\sqrt{1-{\left(\frac{\mathrm{𝑣₀}}{𝑐}\right)}^2}}& \frac{\frac{\mathrm{𝑣₀}}{𝑐}}{\sqrt{1-{\left(\frac{\mathrm{𝑣₀}}{𝑐}\right)}^2}}\\ \frac{\frac{\mathrm{𝑣₀}}{𝑐}}{\sqrt{1-{\left(\frac{\mathrm{𝑣₀}}{𝑐}\right)}^2}}& \frac{1}{\sqrt{1-{\left(\frac{\mathrm{𝑣₀}}{𝑐}\right)}^2}}\end{array}\right)\left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(1)}}\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)\\ & =& \left(\begin{array}{cc}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \tanh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\\ \tanh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\end{array}\right)\left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(1)}}\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)\\ & =& \left(\begin{array}{cc}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\\ \sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\end{array}\right)\left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(1)}}\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)& \text{(52)}\end{array}$$ のようになる。しかし(52)式の変換は原点を原点に移す変換である。今欲しいのはS₍₁₎系の点 $({𝑡}_{\mathrm{(1)}},{𝑥}_{\mathrm{(1)}})=(\mathrm{𝛵₀},0)$ がS₍₀₎系の点 $({𝑡}_{\mathrm{(0)}},{𝑥}_{\mathrm{(0)}})=(\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐},\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}-\frac{{𝑐}^2}{𝑎})$ に対応するような変換である（この対応は(51)式に ${𝑡}_{\mathrm{(1)}}=\mathrm{𝛵₀}$ を代入して求めた）。そのため(52)式を平行移動して、 $$\left(\begin{array}{c}𝑐({𝑡}_{\mathrm{(0)}}-\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐})\\ {𝑥}_{\mathrm{(0)}}-(\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}-\frac{{𝑐}^2}{𝑎})\end{array}\right)=\left(\begin{array}{cc}\cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\\ \sinh \frac{𝑎\mathrm{𝛵₀}}{𝑐}& \cosh \frac{𝑎\mathrm{𝛵₀}}{𝑐}\end{array}\right)\left(\begin{array}{c}𝑐({𝑡}_{\mathrm{(1)}}-\mathrm{𝛵₀})\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)\text{(53)}$$ のようにする。これで ${𝑡}_{\mathrm{(1)}}=\mathrm{𝛵₀}$ のとき専用の変換式が導かれた。下図はこの座標変換の様子を図示したものである。ピンクはS₍₀₎系の座標、緑はS₍₁₎系の座標であり、茶色の太い破線はボブの世界線を表す。

(51)式と同じような適用範囲が狭いあまり役に立たない式がまたできたと思うかもしれないがそうではない。(51)式の適用範囲は ${𝑥}_{\mathrm{(1)}}$ の値が具体的に0であるときに限定されていた。一方、(53)式の適用範囲は ${𝑡}_{\mathrm{(1)}}$ の値が 𝛵₀ であるときに限定されてはいるが、 𝛵₀ の具体的な値は指定していない。もし時刻が変わって ${𝑡}_{\mathrm{(1)}}$ の値が 𝛵₀ でなくなり 𝛵₅ とか 𝛵₈ とかになったとしたら、(53)式の 𝛵₀ を 𝛵₅ とか 𝛵₈ とかに書き換えればその式が使えるのである。ということは(53)式の 𝛵₀ を ${𝑡}_{\mathrm{(1)}}$ に書き換えてしまえばいつでも使える式ができるわけである。そこで(53)式に $\mathrm{𝛵₀}={𝑡}_{\mathrm{(1)}}$ を代入しついでに整理すると、 $$\begin{array}{lll}\hfill \left(\begin{array}{c}𝑐({𝑡}_{\mathrm{(0)}}-\frac{𝑐}{𝑎}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐})\\ {𝑥}_{\mathrm{(0)}}-(\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎})\end{array}\right)& =& \left(\begin{array}{cc}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\end{array}\right)\left(\begin{array}{c}𝑐({𝑡}_{\mathrm{(1)}}-{𝑡}_{\mathrm{(1)}})\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)\\ \hfill \left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(0)}}-\frac{{𝑐}^2}{𝑎}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ {𝑥}_{\mathrm{(0)}}-(\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎})\end{array}\right)& =& \left(\begin{array}{cc}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\end{array}\right)\left(\begin{array}{c}0\\ {𝑥}_{\mathrm{(1)}}\end{array}\right)\\ \hfill \left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(0)}}-\frac{{𝑐}^2}{𝑎}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ {𝑥}_{\mathrm{(0)}}-(\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎})\end{array}\right)& =& \left(\begin{array}{c}{𝑥}_{\mathrm{(1)}}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ {𝑥}_{\mathrm{(1)}}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\end{array}\right)\\ \hfill \left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(0)}}\\ {𝑥}_{\mathrm{(0)}}\end{array}\right)& =& \left(\begin{array}{c}{𝑥}_{\mathrm{(1)}}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}+\frac{{𝑐}^2}{𝑎}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ {𝑥}_{\mathrm{(1)}}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}+(\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎})\end{array}\right)\\ \hfill \left(\begin{array}{c}𝑐{𝑡}_{\mathrm{(0)}}\\ {𝑥}_{\mathrm{(0)}}\end{array}\right)& =& \left(\begin{array}{c}({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ ({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\end{array}\right)& \text{(54)}\end{array}$$ のようになる。これがS₍₀₎系とS₍₁₎系との座標変換である。当然ながら(54)式の変換はもはやローレンツ変換ではなく、何か別の非線形な変換である。

ところで ${𝑥}_{\mathrm{(1)}}=-\frac{{𝑐}^2}{𝑎}$ のときは ${𝑡}_{\mathrm{(1)}}$ の値にかかわらず $({𝑡}_{\mathrm{(0)}},{𝑥}_{\mathrm{(0)}})=(0,-\frac{{𝑐}^2}{𝑎})$ となるし、 ${𝑥}_{\mathrm{(1)}}<-\frac{{𝑐}^2}{𝑎}$ のときは ${𝑡}_{\mathrm{(1)}}$ が増加すると ${𝑡}_{\mathrm{(0)}}$ が減少することになり、ややこしい。そのような面倒な話は扱いたくないので、今後S₍₁₎系では ${𝑥}_{\mathrm{(1)}}>-\frac{{𝑐}^2}{𝑎}$ である領域に限って話を進めることにする。もしS₍₁₎系でアリスの世界線を計算した結果が ${𝑥}_{\mathrm{(1)}}\leqq -\frac{{𝑐}^2}{𝑎}$ になってしまったらもう一度考え直しである。

ここで後々のために(54)式の逆変換を求めておく。(54)式の𝑥成分より、 $$\begin{array}{lll}\hfill {𝑥}_{\mathrm{(0)}}& =& ({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\\ \hfill {𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}& =& ({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \text{(55)}\\ \hfill \frac{{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}}{\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}}& =& {𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎}\end{array}$$ であるから、これを(54)式の𝑐𝑡成分の右辺に代入すると、 $$\begin{array}{lll}\hfill 𝑐{𝑡}_{\mathrm{(0)}}& =& \frac{{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}}{\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill 𝑐{𝑡}_{\mathrm{(0)}}& =& ({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})\tanh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{𝑐{𝑡}_{\mathrm{(0)}}}{{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}}& =& \tanh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \mathrm{artanh}\frac{𝑐{𝑡}_{\mathrm{(0)}}}{{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}}& =& \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{𝑐{𝑡}_{\mathrm{(0)}}}{{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}}& =& 𝑐{𝑡}_{\mathrm{(1)}}& \text{(56)}\end{array}$$ である。$\mathrm{artanh}$ は $\tanh$ の逆関数である。また、[(55)式]²−[(54)式の𝑐𝑡成分]²より、 $$\begin{array}{lll}\hfill {({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2& =& {\left\{({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}}^2-{\left\{({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}}^2\\ \hfill {({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2& =& {({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})}^2({\cosh }^2\frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-{\sinh }^2\frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐})\\ \hfill {({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2& =& {({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})}^2\\ \hfill \pm \sqrt{{({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2}& =& {𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎}\\ \hfill -\frac{{𝑐}^2}{𝑎}\pm \sqrt{{({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2}& =& {𝑥}_{\mathrm{(1)}}\end{array}$$ であるが、今 ${𝑥}_{\mathrm{(1)}}>-\frac{{𝑐}^2}{𝑎}$ だから複号は正を採用し、 $${𝑥}_{\mathrm{(1)}}=\sqrt{{({𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎})}^2-{\left(𝑐{𝑡}_{\mathrm{(0)}}\right)}^2}-\frac{{𝑐}^2}{𝑎}\text{(57)}$$ である。なおこの変換ができるためのS₍₀₎系の変域は $\left|𝑐{𝑡}_{\mathrm{(0)}}\right|<{𝑥}_{\mathrm{(0)}}+\frac{{𝑐}^2}{𝑎}$ である。

ここまでで求めたS₍₁₎系のような座標系をリンドラー座標と呼ぶ。この節の最初のほうで「安直な変換を考えてみる。」と言ったが、今のように時空が平坦で加速度が一定で加速度と速度の方向が同じである特殊な状況であれば、このような安直な方法でうまくいくのである。しかしいつでもこの考え方が通用するわけではない。

計量テンソル

S₍₁₎系の計量テンソル 𝑔_𝜇𝜈 を求める。ミンコフスキー座標S₍₀₎系との変換式が求まっているから、計量テンソルの計算は単に公式に当てはめるだけなので簡単である。具体的には ${𝑔}_{𝜇𝜈}=\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛼}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜇}}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛽}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜈}}{𝜂}_{𝛼𝛽}$ を計算する。この式の右辺は見かけは1個の項だが、実際は ∑ が省略されており、上下にペアで現れる添え字は和をとるという規約が適用される。∑ を省略せずに書けば ${𝑔}_{𝜇𝜈}=\sum _{𝛼=0}^3\sum _{𝛽=0}^3\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛼}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜇}}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛽}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜈}}{𝜂}_{𝛼𝛽}$ でありこれは16個の項から成っている。

まず 𝜂_𝛼𝛽 はミンコフスキー計量でありその値は $$\left({𝜂}_{𝛼𝛽}\right)=\left(\begin{array}{cccc}{𝜂}_{00}& {𝜂}_{01}& {𝜂}_{02}& {𝜂}_{03}\\ {𝜂}_{10}& {𝜂}_{11}& {𝜂}_{12}& {𝜂}_{13}\\ {𝜂}_{20}& {𝜂}_{21}& {𝜂}_{22}& {𝜂}_{23}\\ {𝜂}_{30}& {𝜂}_{31}& {𝜂}_{32}& {𝜂}_{33}\end{array}\right)=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{(58)}$$ である。符号を逆に定義する流儀もあるので、気を付けてほしい。

次に座標変換の偏微分 $\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛼}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜇}}$ を求める。S₍₀₎系とS₍₁₎系との座標変換の式は(54)式で導出したが、4成分とも省略せずに書けば $$\{\begin{array}{lll}\hfill 𝑐{𝑡}_{\mathrm{(0)}}& =& ({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill {𝑥}_{\mathrm{(0)}}& =& ({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\\ \hfill {𝑦}_{\mathrm{(0)}}& =& {𝑦}_{\mathrm{(1)}}\\ \hfill {𝑧}_{\mathrm{(0)}}& =& {𝑧}_{\mathrm{(1)}}\end{array}\text{(59)}$$ であるから、その偏微分は $$\begin{array}{lll}\hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& =& \frac{\partial \left(𝑐{𝑡}_{\mathrm{(0)}}\right)}{\partial \left(𝑐{𝑡}_{\mathrm{(1)}}\right)}\\ & =& \frac{1}{𝑐}\frac{\partial }{{\mathrm{\partial 𝑡}}_{\mathrm{(1)}}}\left\{\right({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎}\left)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}\\ & =& \frac{1}{𝑐}({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\frac{𝑎}{𝑐}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ & =& (\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& =& \frac{\partial \left(𝑐{𝑡}_{\mathrm{(0)}}\right)}{{\mathrm{\partial 𝑥}}_{\mathrm{(1)}}}\\ & =& \frac{\partial }{{\mathrm{\partial 𝑥}}_{\mathrm{(1)}}}\left\{\right({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎}\left)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}\\ & =& \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& =& \frac{{\mathrm{\partial 𝑥}}_{\mathrm{(0)}}}{\partial \left(𝑐{𝑡}_{\mathrm{(1)}}\right)}\\ & =& \frac{1}{𝑐}\frac{\partial }{{\mathrm{\partial 𝑡}}_{\mathrm{(1)}}}\left\{\right({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\}\\ & =& \frac{1}{𝑐}({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\frac{𝑎}{𝑐}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ & =& (\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& =& \frac{{\mathrm{\partial 𝑥}}_{\mathrm{(0)}}}{{\mathrm{\partial 𝑥}}_{\mathrm{(1)}}}\\ & =& \frac{\partial }{{\mathrm{\partial 𝑥}}_{\mathrm{(1)}}}\left\{\right({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}-\frac{{𝑐}^2}{𝑎}\}\\ & =& \cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ \hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^2}& =& \frac{{\mathrm{\partial 𝑦}}_{\mathrm{(0)}}}{{\mathrm{\partial 𝑦}}_{\mathrm{(1)}}}\\ & =& \frac{\partial }{{\mathrm{\partial 𝑦}}_{\mathrm{(1)}}}{𝑦}_{\mathrm{(1)}}\\ & =& 1\\ \hfill \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^3}& =& \frac{{\mathrm{\partial 𝑧}}_{\mathrm{(0)}}}{{\mathrm{\partial 𝑧}}_{\mathrm{(1)}}}\\ & =& \frac{\partial }{{\mathrm{\partial 𝑧}}_{\mathrm{(1)}}}{𝑧}_{\mathrm{(1)}}\\ & =& 1\end{array}$$ であり、その他の成分は0である。まとめると、 $$\left(\begin{array}{cccc}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^2}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^3}\\ \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^2}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^3}\\ \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^2}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^3}\\ \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^2}& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^3}\end{array}\right)=\left(\begin{array}{cccc}(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& 0& 0\\ (\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& \cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{(60)}$$ のようになる。

これらを使って計量テンソルが求められる。例えば第00成分は、 $$\begin{array}{lll}\hfill {𝑔}_{00}& =& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛼}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛽}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{𝛼𝛽}\\ & =& \phantom{+}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{00}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{01}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{02}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{03}\\ & & +\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{10}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{11}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{12}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{13}\\ & & +\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{20}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{21}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{22}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{23}\\ & & +\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{30}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{31}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^2}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{32}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^3}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{33}\\ & =& \phantom{+}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{00}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0\cdot 0+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0\cdot 0\\ & & +\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}{𝜂}_{11}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0\cdot 0+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0\cdot 0\\ & & +0\cdot \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+0\cdot \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+0\cdot 0\cdot {𝜂}_{22}+0\cdot 0\cdot 0\\ & & +0\cdot \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+0\cdot \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\cdot 0+0\cdot 0\cdot 0+0\cdot 0\cdot {𝜂}_{33}\\ & =& {\left(\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\right)}^2{𝜂}_{00}+{\left(\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\right)}^2{𝜂}_{11}\\ & =& {\left\{\right(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}}^2\cdot (-1)+{\left\{\right(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}}^2\cdot 1\\ & =& {(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2(-{\cosh }^2\frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}+{\sinh }^2\frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐})\\ & =& -{(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2\end{array}$$ のようになる。3個目の等号では(58)・(60)式のうち0であるものだけを代入した。5個目の等号では(58)・(60)式の残りを代入した。

他の成分も同様に計算される。途中の計算式で0になる項は面倒なのでもう書かない。

また、計量テンソルは対称テンソルであるから、 $$\begin{array}{lll}\hfill {𝑔}_{10}={𝑔}_{01}& =& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛼}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^{𝛽}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}{𝜂}_{𝛼𝛽}\\ & =& \frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^0}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}{𝜂}_{00}+\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^0}\frac{{{\mathrm{\partial 𝑋}}_{\mathrm{(0)}}}^1}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}{𝜂}_{11}\\ & =& \left\{\right(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}\left(\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right)\cdot (-1)+\left\{\right(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right\}\left(\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\right)\cdot 1\\ & =& -(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}+(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\sinh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\cosh \frac{𝑎{𝑡}_{\mathrm{(1)}}}{𝑐}\\ & =& 0\end{array}$$ であり、これら以外の成分は途中の計算式のすべての項が0であるから結果も0である。まとめると、 $$\left({𝑔}_{𝜇𝜈}\right)=\left(\begin{array}{cccc}{𝑔}_{00}& {𝑔}_{01}& {𝑔}_{02}& {𝑔}_{03}\\ {𝑔}_{10}& {𝑔}_{11}& {𝑔}_{12}& {𝑔}_{13}\\ {𝑔}_{20}& {𝑔}_{21}& {𝑔}_{22}& {𝑔}_{23}\\ {𝑔}_{30}& {𝑔}_{31}& {𝑔}_{32}& {𝑔}_{33}\end{array}\right)=\left(\begin{array}{cccc}-{(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{(61)}$$ である。また、反変成分は共変成分の逆行列であるが(61)式は対角行列であるから対角成分を逆数にすればよくて、 $$\left({𝑔}^{𝜇𝜈}\right)=\left(\begin{array}{cccc}{𝑔}^{00}& {𝑔}^{01}& {𝑔}^{02}& {𝑔}^{03}\\ {𝑔}^{10}& {𝑔}^{11}& {𝑔}^{12}& {𝑔}^{13}\\ {𝑔}^{20}& {𝑔}^{21}& {𝑔}^{22}& {𝑔}^{23}\\ {𝑔}^{30}& {𝑔}^{31}& {𝑔}^{32}& {𝑔}^{33}\end{array}\right)=\left(\begin{array}{cccc}-\frac{1}{{(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2}& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{(62)}$$ である。

クリストッフェル記号

S₍₁₎系のクリストッフェル記号 𝛤^𝜆_𝜇𝜈 を求める。単に公式に当てはめるだけであり、具体的には $𝛤^{𝜆}{}_{𝜇}{}_{𝜈}=\frac{1}{2}{𝑔}^{𝜆𝜌}(\frac{{\mathrm{\partial 𝑔}}_{𝜌𝜇}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜈}}+\frac{{\mathrm{\partial 𝑔}}_{𝜌𝜈}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜇}}-\frac{{\mathrm{\partial 𝑔}}_{𝜇𝜈}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜌}})$ を計算する。この式の右辺は見かけは1個（かっこを展開すれば3個）の項だが、実際は ∑ が省略されており、上下にペアで現れる添え字は和をとるという規約が適用される。∑ を省略せずに書けば $𝛤^{𝜆}{}_{𝜇}{}_{𝜈}=\frac{1}{2}\sum _{𝜌=0}^3{𝑔}^{𝜆𝜌}(\frac{{\mathrm{\partial 𝑔}}_{𝜌𝜇}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜈}}+\frac{{\mathrm{\partial 𝑔}}_{𝜌𝜈}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜇}}-\frac{{\mathrm{\partial 𝑔}}_{𝜇𝜈}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^{𝜌}})$ でありこれは4個（かっこを展開すれば12個）の項から成っている。

(61)式より、計量テンソルの偏微分のうち0でないものは $$\begin{array}{lll}\hfill \frac{{\mathrm{\partial 𝑔}}_{00}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}& =& \frac{\partial }{{\mathrm{\partial 𝑥}}_{\mathrm{(1)}}}\{-{(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2\}\\ & =& -\frac{2𝑎}{{𝑐}^2}(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\end{array}$$ だけである。これ以外の成分はすべて0である。

したがって、クリストッフェル記号のうち0でないものは $$\begin{array}{lll}\hfill 𝛤^0{}_0{}_1=𝛤^0{}_1{}_0& =& \frac{1}{2}{𝑔}^{00}\left(\frac{{\mathrm{\partial 𝑔}}_{00}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1}\right)\\ & =& \frac{1}{2}\{-\frac{1}{{(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)}^2}\}\{-\frac{2𝑎}{{𝑐}^2}(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\right\}\\ & =& \frac{𝑎}{{𝑐}^2}\frac{1}{\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1}\\ & =& \frac{1}{{𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎}}& \text{(63)}\\ \hfill 𝛤^1{}_0{}_0& =& \frac{1}{2}{𝑔}^{11}(-\frac{{\mathrm{\partial 𝑔}}_{00}}{{{\mathrm{\partial 𝑋}}_{\mathrm{(1)}}}^1})\\ & =& \frac{1}{2}\cdot 1\cdot \left\{\frac{2𝑎}{{𝑐}^2}\right(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1\left)\right\}\\ & =& \frac{𝑎}{{𝑐}^2}(\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(1)}}+1)\\ & =& \frac{{𝑎}^2}{{𝑐}^4}({𝑥}_{\mathrm{(1)}}+\frac{{𝑐}^2}{𝑎})& \text{(64)}\end{array}$$ である。これら以外の成分はすべて0である。