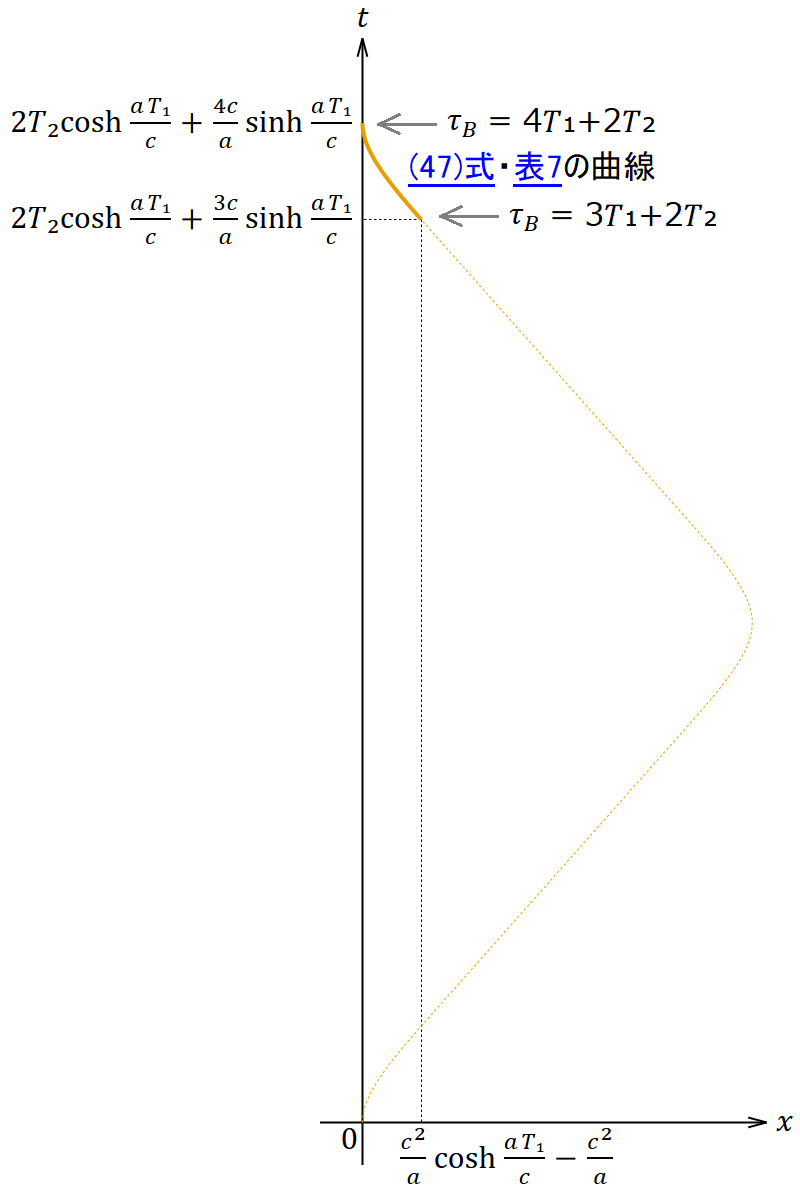A.3. 折り返し局面

次に往路の減速を始めてから往路が終了するまで、およびその後直ちに復路に突入してから復路の加速をやめるまでの期間（これを「折り返し局面」とする。）を考える。往路から復路に切り替わる前後で加速度は一定だからまとめて扱うのである。

この局面の開始時は往路惰行局面の終了時と同じであるから、ボブの固有時は定義により 𝑇₁+𝑇₂ であり、A.2節の最後で計算したようにそのときの座標時は $\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの速度は $𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの位置は $𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}$ である。これが初期条件となる。

次にボブが満たすべき微分方程式の一般解を求める。加速度が一定の 𝑎 である場合の解はA.1節の出発局面の表2で導出済みである。そしてその解は 𝑎 が正でも負でも成り立つのであった。今の折り返し局面では加速度が一定の −𝑎 (𝑎 > 0) であるから、以下のように表2の 𝑎 を −𝑎 に置き換えるだけでよい。

ボブの固有時は(10)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill {𝜏}_{𝐵}& =& \frac{𝑐}{-𝑎}\mathrm{arsinh}\frac{-𝑎𝑡+\mathrm{𝐾₀}}{𝑐}+\mathrm{𝐾₁}\\ & =& -\frac{𝑐}{𝑎}\mathrm{arsinh}(-\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐})+\mathrm{𝐾₁}\\ & =& \frac{𝑐}{𝑎}\mathrm{arsinh}\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}+\mathrm{𝐾₁}& \text{(22)}\end{array}$$ となり、ボブの速度は(8)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill 𝑣\left(𝑡\right)& =& \frac{-𝑎𝑡+\mathrm{𝐾₀}}{\sqrt{1+{\left(\frac{-𝑎𝑡+\mathrm{𝐾₀}}{𝑐}\right)}^2}}\\ & =& -\frac{𝑎𝑡-\mathrm{𝐾₀}}{\sqrt{1+{(-\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐})}^2}}\\ & =& -\frac{𝑎𝑡-\mathrm{𝐾₀}}{\sqrt{1+{\left(\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}\right)}^2}}& \text{(23)}\end{array}$$ となり、ボブの位置は(14)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill 𝑥\left(𝑡\right)& =& \frac{{𝑐}^2}{-𝑎}\sqrt{1+{\left(\frac{-𝑎𝑡+\mathrm{𝐾₀}}{𝑐}\right)}^2}+\mathrm{𝐾₂}\\ & =& -\frac{{𝑐}^2}{𝑎}\sqrt{1+{(-\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐})}^2}+\mathrm{𝐾₂}\\ & =& -\frac{{𝑐}^2}{𝑎}\sqrt{1+{\left(\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}\right)}^2}+\mathrm{𝐾₂}& \text{(24)}\end{array}$$ となる。また、 𝜏_𝐵 によるパラメータ表示をすると、座標時は(13)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill 𝑡& =& \frac{𝑐}{-𝑎}\sinh \frac{-𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}-\frac{\mathrm{𝐾₀}}{-𝑎}\\ & =& -\frac{𝑐}{𝑎}\{-\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}\}+\frac{\mathrm{𝐾₀}}{𝑎}\\ & =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}& \text{(25)}\end{array}$$ となり、ボブの速度は(15)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill 𝑣\left(𝑡\right)& =& 𝑐\tanh \frac{-𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}\\ & =& -𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}& \text{(26)}\end{array}$$ となり、ボブの位置は(16)式の 𝑎 を −𝑎 に置き換えて $$\begin{array}{lll}\hfill 𝑥\left(𝑡\right)& =& \frac{{𝑐}^2}{-𝑎}\cosh \frac{-𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}\\ & =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}& \text{(27)}\end{array}$$ となる。

次に初期条件を使って積分定数 𝐾₀, 𝐾₁, 𝐾₂ を定める。まず(26)式の 𝑣(𝑡) と 𝜏_𝐵 に初期条件を代入すると、 $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& -𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}& \text{←}\text{(26)式}\\ \hfill 𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& -𝑐\tanh \frac{𝑎\left\{\right(\mathrm{𝑇₁}+\mathrm{𝑇₂})-\mathrm{𝐾₁}\}}{𝑐}& \text{←初期条件を代入した。}\\ \hfill \tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& -\tanh \frac{𝑎(\mathrm{𝑇₁}+\mathrm{𝑇₂}-\mathrm{𝐾₁})}{𝑐}\\ \hfill \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& -\frac{𝑎(\mathrm{𝑇₁}+\mathrm{𝑇₂}-\mathrm{𝐾₁})}{𝑐}\\ \hfill \mathrm{𝑇₁}& =& -(\mathrm{𝑇₁}+\mathrm{𝑇₂}-\mathrm{𝐾₁})\\ \hfill \mathrm{𝑇₁}& =& -\mathrm{𝑇₁}-\mathrm{𝑇₂}+\mathrm{𝐾₁}\\ \hfill 2\mathrm{𝑇₁}+\mathrm{𝑇₂}& =& \mathrm{𝐾₁}& \text{(28)}\end{array}$$ のように 𝐾₁ が定まる。(25)式の 𝑡 と 𝜏_𝐵 に初期条件を代入し 𝐾₁ に(28)式を代入すると、 $$\begin{array}{llll}\hfill 𝑡& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}& \text{←}\text{(25)式}\\ \hfill \mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎\left\{\right(\mathrm{𝑇₁}+\mathrm{𝑇₂})-(2\mathrm{𝑇₁}+\mathrm{𝑇₂}\left)\right\}}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}& \text{←初期条件と}\text{(28)式}\text{を代入した。}\\ \hfill \mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑐}{𝑎}\sinh \frac{-𝑎\mathrm{𝑇₁}}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}\\ \hfill \mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& -\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}\\ \hfill \mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{\mathrm{𝐾₀}}{𝑎}\\ \hfill 𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₀}& \text{(29)}\end{array}$$ のように 𝐾₀ が定まる。(27)式の 𝑥(𝑡) と 𝜏_𝐵 に初期条件を代入し 𝐾₁ に(28)式を代入すると、 $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}& \text{←}\text{(27)式}\\ \hfill 𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\left\{\right(\mathrm{𝑇₁}+\mathrm{𝑇₂})-(2\mathrm{𝑇₁}+\mathrm{𝑇₂}\left)\right\}}{𝑐}+\mathrm{𝐾₂}& \text{←初期条件と}\text{(28)式}\text{を代入した。}\\ \hfill 𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{-𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₂}\\ \hfill 𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₂}\\ \hfill 𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& \mathrm{𝐾₂}& \text{(30)}\end{array}$$ のように 𝐾₂ が定まる。

以上で積分定数の値が決まったので、特殊解を求める。ボブの固有時は(22)式より $$\begin{array}{llll}\hfill {𝜏}_{𝐵}& =& \frac{𝑐}{𝑎}\mathrm{arsinh}\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}+\mathrm{𝐾₁}& \text{←}\text{(22)式}\\ & =& \frac{𝑐}{𝑎}\mathrm{arsinh}\frac{𝑎𝑡-(𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}+(2\mathrm{𝑇₁}+\mathrm{𝑇₂})& \text{←}\text{(29)}\text{・}\text{(28)式}\text{を代入した。}\\ & =& \frac{𝑐}{𝑎}\mathrm{arsinh}\{\frac{𝑎}{𝑐}(𝑡-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\}+2\mathrm{𝑇₁}+\mathrm{𝑇₂}& \text{(31)}\end{array}$$ となり、ボブの速度は(23)式より $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& -\frac{𝑎𝑡-\mathrm{𝐾₀}}{\sqrt{1+{\left(\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}\right)}^2}}& \text{←}\text{(23)式}\\ & =& -\frac{𝑎𝑡-(𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{\sqrt{1+{\left\{\frac{𝑎𝑡-(𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}\right\}}^2}}& \text{←}\text{(29)式}\text{を代入した。}\\ & =& -\frac{𝑎(𝑡-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\sqrt{1+{\left\{\frac{𝑎}{𝑐}\right(𝑡-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\}}^2}}& \text{(32)}\end{array}$$ となり、ボブの位置は(24)式より $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& -\frac{{𝑐}^2}{𝑎}\sqrt{1+{\left(\frac{𝑎𝑡-\mathrm{𝐾₀}}{𝑐}\right)}^2}+\mathrm{𝐾₂}& \text{←}\text{(24)式}\\ & =& -\frac{{𝑐}^2}{𝑎}\sqrt{1+{\left\{\frac{𝑎𝑡-(𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}\right\}}^2}+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})& \text{←}\text{(29)}\text{・}\text{(30)式}\text{を代入した。}\\ & =& -\frac{{𝑐}^2}{𝑎}\sqrt{1+{\{\frac{𝑎}{𝑐}(𝑡-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\}}^2}+𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& \text{(33)}\end{array}$$ となる。また、 𝜏_𝐵 によるパラメータ表示をすると、座標時は(25)式より $$\begin{array}{llll}\hfill 𝑡& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\frac{\mathrm{𝐾₀}}{𝑎}& \text{←}\text{(25)式}\\ & =& \frac{𝑐}{𝑎}\sinh \frac{𝑎\{{𝜏}_{𝐵}-(2\mathrm{𝑇₁}+\mathrm{𝑇₂}\left)\right\}}{𝑐}+\frac{𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{𝑎}& \text{←}\text{(28)}\text{・}\text{(29)式}\text{を代入した。}\\ & =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-2\mathrm{𝑇₁}-\mathrm{𝑇₂})}{𝑐}+\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(34)}\end{array}$$ となり、ボブの速度は(26)式より $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& -𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}& \text{←}\text{(26)式}\\ & =& -𝑐\tanh \frac{𝑎\{{𝜏}_{𝐵}-(2\mathrm{𝑇₁}+\mathrm{𝑇₂}\left)\right\}}{𝑐}& \text{←}\text{(28)式}\text{を代入した。}\\ & =& -𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-2\mathrm{𝑇₁}-\mathrm{𝑇₂})}{𝑐}& \text{(35)}\end{array}$$ となり、ボブの位置は(27)式より $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}& \text{←}\text{(27)式}\\ & =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\{{𝜏}_{𝐵}-(2\mathrm{𝑇₁}+\mathrm{𝑇₂}\left)\right\}}{𝑐}+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})& \text{←}\text{(28)}\text{・}\text{(30)式}\text{を代入した。}\\ & =& -\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-2\mathrm{𝑇₁}-\mathrm{𝑇₂})}{𝑐}+𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& \text{(36)}\end{array}$$ となる。

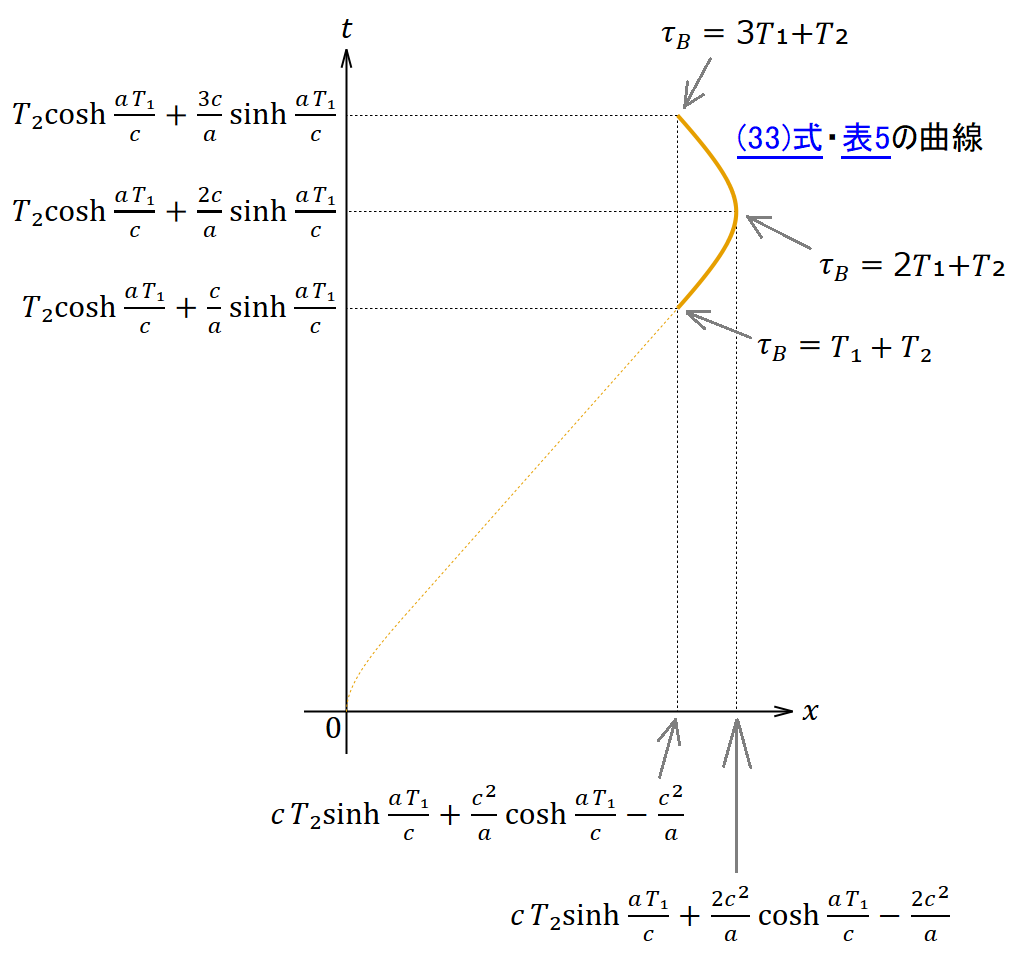
(31)〜(36)式をまとめたものが表5だ。だんだん式が長くなってきたが、大部分は定数であって変数は 𝑡 または 𝜏_𝐵 だけなので、それほどややこしい関数ではない。単なる双曲線である。

ボブの固有時が 𝜏_𝐵 = 2𝑇₁+𝑇₂ であるときに往路から復路に切り替わることが期待されるが、本当にそうなっているか確認しよう。(35)式に 𝜏_𝐵 = 2𝑇₁+𝑇₂ を代入すると 速度=0 となり、この瞬間に速度が正から負に変わることがわかるので、確かにそうなっている。このとき、(34)式より座標時は $\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ であり、(36)式よりボブの位置は $𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2{𝑐}^2}{𝑎}$ である。この位置はボブがアリスから最も遠くに離れたときの位置である。

折り返し局面の終了時では、 𝜏_𝐵 = 3𝑇₁+𝑇₂ であるからこれを表5の解に代入すると、座標時は $\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの速度は $-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの位置は $𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}$ である。

A.4. 復路惰行局面

次に復路の加速をやめてから減速を始めるまでの、加速度が0である期間（これを「復路惰行局面」とする。）を考える。

この局面の開始時は折り返し局面の終了時と同じであるから、ボブの固有時は定義により 3𝑇₁+𝑇₂ であり、A.3節の最後で計算したようにそのときの座標時は $\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの速度は $-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの位置は $𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}$ である。これが初期条件となる。

復路惰行局面を通して加速度が0であるから、速度 $𝑣\left(𝑡\right)=-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ は一定である。これは往路惰行局面での速度と同じ大きさで符号が逆である。固有時を求める式は(3)式のように、速度 𝑣(𝑡) についてはその2乗 {𝑣(𝑡)}² しか出てこないので、速度の大きさが同じであれば符号が逆でも固有時の式は同じである。したがって固有時 𝜏_𝐵 は往路惰行局面の(17)式と同じ計算により $${𝜏}_{𝐵}=\frac{𝑡}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\mathrm{𝐾₃}\text{（𝐾₃は積分定数）}\text{(37)}$$ となる。初期条件は $𝑡=\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ のとき 𝜏_𝐵 = 3𝑇₁+𝑇₂ であるからこれを(37)式に代入すると $$\begin{array}{lll}\hfill 3\mathrm{𝑇₁}+\mathrm{𝑇₂}& =& \frac{\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\mathrm{𝐾₃}\\ \hfill 3\mathrm{𝑇₁}+\mathrm{𝑇₂}& =& \mathrm{𝑇₂}+\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₃}\\ \hfill 3\mathrm{𝑇₁}-\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₃}\end{array}$$ のように積分定数 𝐾₃ が定まる。これを(37)式に代入すると固有時は $${𝜏}_{𝐵}=\frac{𝑡}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+3\mathrm{𝑇₁}-\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\text{(38)}$$ となる。(38)式を 𝑡 について解くと $$\begin{array}{lll}\hfill \frac{𝑡}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+3\mathrm{𝑇₁}-\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {𝜏}_{𝐵}\\ \hfill \frac{𝑡}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}& =& {𝜏}_{𝐵}-3\mathrm{𝑇₁}+\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ \hfill 𝑡& =& ({𝜏}_{𝐵}-3\mathrm{𝑇₁})\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& ({𝜏}_{𝐵}-3\mathrm{𝑇₁})\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(39)}\end{array}$$ である。速度 𝑣(𝑡) が 𝑡 によらず一定であるから、位置 𝑥(𝑡) は座標時 𝑡 の1次関数になるので速度と初期条件の座標を使って $$\begin{array}{lll}\hfill 𝑥\left(𝑡\right)& =& (𝑡-\boxed{\text{𝑡 の初期値}})𝑣\left(𝑡\right)+\boxed{\text{𝑥(𝑡) の初期値}}\\ & =& \{𝑡-(\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}(-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})\\ & =& -𝑐(𝑡-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})\\ & =& -𝑐(𝑡-\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+𝑐\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})\\ & =& -𝑐(𝑡-\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+(𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎})\\ & =& -𝑐(𝑡-\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+2𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& \text{(40)}\end{array}$$ と表される。 ついでに、(39)式を(40)式に代入して 𝑥(𝑡) を 𝜏_𝐵 で表してみる。

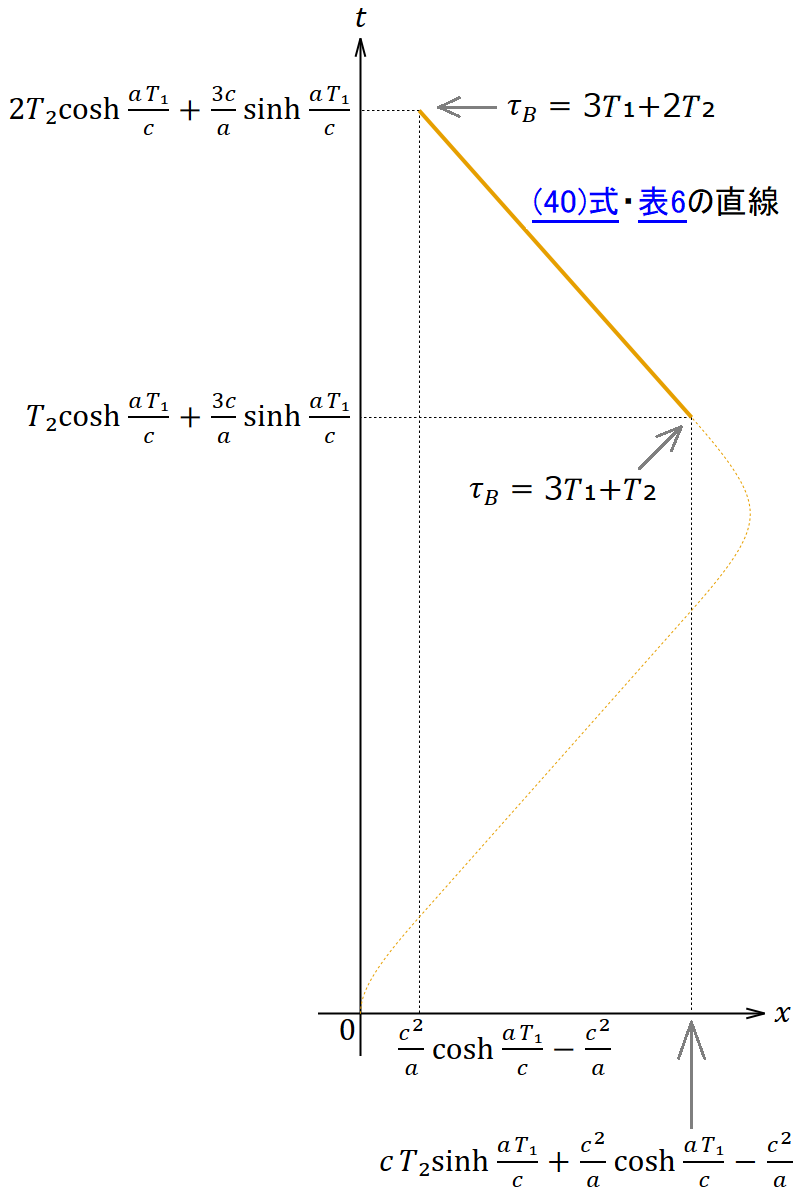
(38)〜(41)式をまとめたものが表6だ。

復路惰行局面の終了時では、 𝜏_𝐵 = 3𝑇₁+2𝑇₂ であるからこれを表6の解に代入すると、座標時は $2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの速度は $-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの位置は $\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}$ である。

A.5. 帰還局面

最後に復路の減速を始めてから復路が終了するまでの期間（これを「帰還局面」とする。）を考える。

この局面の開始時は復路惰行局面の終了時と同じであるから、ボブの固有時は定義により 3𝑇₁+2𝑇₂ であり、A.4節の最後で計算したようにそのときの座標時は $2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの速度は $-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、ボブの位置は $\frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}$ である。これが初期条件となる。

今の帰還局面では加速度が一定の 𝑎 であり、これは出発局面と同じであるから、ボブが満たすべき微分方程式も出発局面とまったく同じである。したがって一般解はA.1節の出発局面の表2で導出した(13)・(10)・(8)・(15)・(14)・(16)式をそのまま使えばよい。

次に初期条件を使って積分定数 𝐾₀, 𝐾₁, 𝐾₂ を定める。まず(15)式の 𝑣(𝑡) と 𝜏_𝐵 に初期条件を代入すると、 $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& 𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}& \text{←}\text{(15)式}\\ \hfill -𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& 𝑐\tanh \frac{𝑎\left\{\right(3\mathrm{𝑇₁}+2\mathrm{𝑇₂})-\mathrm{𝐾₁}\}}{𝑐}& \text{←初期条件を代入した。}\\ \hfill -\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \tanh \frac{𝑎(3\mathrm{𝑇₁}+2\mathrm{𝑇₂}-\mathrm{𝐾₁})}{𝑐}\\ \hfill -\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑎(3\mathrm{𝑇₁}+2\mathrm{𝑇₂}-\mathrm{𝐾₁})}{𝑐}\\ \hfill -\mathrm{𝑇₁}& =& 3\mathrm{𝑇₁}+2\mathrm{𝑇₂}-\mathrm{𝐾₁}\\ \hfill \mathrm{𝐾₁}& =& 4\mathrm{𝑇₁}+2\mathrm{𝑇₂}& \text{(42)}\end{array}$$ のように 𝐾₁ が定まる。(13)式の 𝑡 と 𝜏_𝐵 に初期条件を代入し 𝐾₁ に(42)式を代入すると、 $$\begin{array}{llll}\hfill 𝑡& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}-\frac{\mathrm{𝐾₀}}{𝑎}& \text{←}\text{(13)式}\\ \hfill 2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎\left\{\right(3\mathrm{𝑇₁}+2\mathrm{𝑇₂})-(4\mathrm{𝑇₁}+2\mathrm{𝑇₂}\left)\right\}}{𝑐}-\frac{\mathrm{𝐾₀}}{𝑎}& \text{←初期条件と}\text{(42)式}\text{を代入した。}\\ \hfill 2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑐}{𝑎}\sinh \frac{-𝑎\mathrm{𝑇₁}}{𝑐}-\frac{\mathrm{𝐾₀}}{𝑎}\\ \hfill 2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{3𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& -\frac{𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{\mathrm{𝐾₀}}{𝑎}\\ \hfill \frac{\mathrm{𝐾₀}}{𝑎}& =& -2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{4𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ \hfill \mathrm{𝐾₀}& =& -2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(43)}\end{array}$$ のように 𝐾₀ が定まる。(16)式の 𝑥(𝑡) と 𝜏_𝐵 に初期条件を代入し 𝐾₁ に(42)式を代入すると、 $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}& \text{←}\text{(16)式}\\ \hfill \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\left\{\right(3\mathrm{𝑇₁}+2\mathrm{𝑇₂})-(4\mathrm{𝑇₁}+2\mathrm{𝑇₂}\left)\right\}}{𝑐}+\mathrm{𝐾₂}& \text{←初期条件と}\text{(42)式}\text{を代入した。}\\ \hfill \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& \frac{{𝑐}^2}{𝑎}\cosh \frac{-𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₂}\\ \hfill \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎}& =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₂}\\ \hfill -\frac{{𝑐}^2}{𝑎}& =& \mathrm{𝐾₂}& \text{(44)}\end{array}$$ のように 𝐾₂ が定まる。

以上で積分定数の値が決まったので、特殊解を求める。ボブの固有時は(10)式より $$\begin{array}{llll}\hfill {𝜏}_{𝐵}& =& \frac{𝑐}{𝑎}\mathrm{arsinh}\frac{𝑎𝑡+\mathrm{𝐾₀}}{𝑐}+\mathrm{𝐾₁}& \text{←}\text{(10)式}\\ & =& \frac{𝑐}{𝑎}\mathrm{arsinh}\frac{𝑎𝑡+(-2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}+4\mathrm{𝑇₁}+2\mathrm{𝑇₂}& \text{←}\text{(43)}\text{・}\text{(42)式}\text{を代入した。}\\ & =& \frac{𝑐}{𝑎}\mathrm{arsinh}\left\{\frac{𝑎}{𝑐}\right(𝑡-2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-4\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\}+4\mathrm{𝑇₁}+2\mathrm{𝑇₂}& \text{(45)}\end{array}$$ となり、ボブの速度は(8)式より $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& \frac{𝑎𝑡+\mathrm{𝐾₀}}{\sqrt{1+{\left(\frac{𝑎𝑡+\mathrm{𝐾₀}}{𝑐}\right)}^2}}& \text{←}\text{(8)式}\\ & =& \frac{𝑎𝑡+(-2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{\sqrt{1+{\left\{\frac{𝑎𝑡+(-2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}\right\}}^2}}& \text{←}\text{(43)式を}\text{代入した。}\\ & =& \frac{𝑎(𝑡-2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\sqrt{1+{\left\{\frac{𝑎}{𝑐}(𝑡-2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-4\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\right\}}^2}}& \text{(46)}\end{array}$$ となり、ボブの位置は(14)式より $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& \frac{{𝑐}^2}{𝑎}\sqrt{1+{\left(\frac{𝑎𝑡+\mathrm{𝐾₀}}{𝑐}\right)}^2}+\mathrm{𝐾₂}& \text{←}\text{(14)式}\\ & =& \frac{{𝑐}^2}{𝑎}\sqrt{1+{\left\{\frac{𝑎𝑡+(-2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{𝑐}\right\}}^2}-\frac{{𝑐}^2}{𝑎}& \text{←}\text{(43)}\text{・}\text{(44)式}\text{を代入した。}\\ & =& \frac{{𝑐}^2}{𝑎}\sqrt{1+{\{\frac{𝑎}{𝑐}(𝑡-2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})-4\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\}}^2}-\frac{{𝑐}^2}{𝑎}& \text{(47)}\end{array}$$ となる。また、 𝜏_𝐵 によるパラメータ表示をすると、座標時は(13)式より $$\begin{array}{llll}\hfill 𝑡& =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}-\frac{\mathrm{𝐾₀}}{𝑎}& \text{←}\text{(13)式}\\ & =& \frac{𝑐}{𝑎}\sinh \frac{𝑎\{{𝜏}_{𝐵}-(4\mathrm{𝑇₁}+2\mathrm{𝑇₂}\left)\right\}}{𝑐}-\frac{-2𝑎\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-4𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{𝑎}& \text{←}\text{(42)}\text{・}\text{(43)式}\text{を代入した。}\\ & =& \frac{𝑐}{𝑎}\sinh \frac{𝑎({𝜏}_{𝐵}-4\mathrm{𝑇₁}-2\mathrm{𝑇₂})}{𝑐}+2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{4𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(48)}\end{array}$$ となり、ボブの速度は(15)式より $$\begin{array}{llll}\hfill 𝑣\left(𝑡\right)& =& 𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}& \text{←}\text{(15)式}\\ & =& 𝑐\tanh \frac{𝑎\{{𝜏}_{𝐵}-(4\mathrm{𝑇₁}+2\mathrm{𝑇₂}\left)\right\}}{𝑐}& \text{←}\text{(42)式}\text{を代入した。}\\ & =& 𝑐\tanh \frac{𝑎({𝜏}_{𝐵}-4\mathrm{𝑇₁}-2\mathrm{𝑇₂})}{𝑐}& \text{(49)}\end{array}$$ となり、ボブの位置は(16)式より $$\begin{array}{llll}\hfill 𝑥\left(𝑡\right)& =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-\mathrm{𝐾₁})}{𝑐}+\mathrm{𝐾₂}& \text{←}\text{(16)式}\\ & =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎\{{𝜏}_{𝐵}-(4\mathrm{𝑇₁}-2\mathrm{𝑇₂}\left)\right\}}{𝑐}-\frac{{𝑐}^2}{𝑎}& \text{←}\text{(28)}\text{・}\text{(30)式}\text{を代入した。}\\ & =& \frac{{𝑐}^2}{𝑎}\cosh \frac{𝑎({𝜏}_{𝐵}-4\mathrm{𝑇₁}-2\mathrm{𝑇₂})}{𝑐}-\frac{{𝑐}^2}{𝑎}& \text{(50)}\end{array}$$ となる。

(45)〜(50)式をまとめたものが表7だ。

ボブの固有時が 𝜏_𝐵 = 4𝑇₁+2𝑇₂ であるときに全行程が終了し、このときボブは家に静止していることが期待されるが、本当にそうなっているか確認しよう。(49)式に 𝜏_𝐵 = 4𝑇₁+2𝑇₂ を代入すると 速度=0 となり、(50)式に 𝜏_𝐵 = 4𝑇₁+2𝑇₂ を代入すると 位置=0 となるので、確かにそうなっている。このとき、(48)式より座標時は $2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{4𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ である。

以上の計算により、ボブが出発局面の最初から帰還局面の最後まで合計 4𝑇₁+2𝑇₂ の時間をかけて移動して戻ってくる間に、アリスにとっては $2\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{4𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ だけ時間が進むという主張が導かれた。ここまで延々と計算してようやく表1の左半分が算出できた。まだ半分、しかも楽なほうの半分である。