B.2. 往路惰行局面

運動方程式

アリスの速度はこの局面を通して一定である。その3次元的な速度 𝑣 を求める。今は(100)式より4元速度の第2・3成分（𝑦, 𝑧 成分）は0であるから、ミンコフスキー座標における4元速度の定義により次のような関係を満たす。

$$\begin{array}{l}{{𝑢}_{\mathrm{(2)}}}^0=\frac{𝑐}{\sqrt{1-{\left(\frac{𝑣}{𝑐}\right)}^2}}\text{(101)}\\ {{𝑢}_{\mathrm{(2)}}}^1=\frac{𝑣}{\sqrt{1-{\left(\frac{𝑣}{𝑐}\right)}^2}}\text{(102)}\end{array}$$

(102)式に(100)式の第1成分を代入すると、 $$\begin{array}{lll}\hfill -𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑣}{\sqrt{1-{\left(\frac{𝑣}{𝑐}\right)}^2}}\\ \hfill -\sqrt{1-{\left(\frac{𝑣}{𝑐}\right)}^2}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{𝑣}{𝑐}\\ \hfill \{1-{\left(\frac{𝑣}{𝑐}\right)}^2\}{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {\left(\frac{𝑣}{𝑐}\right)}^2\\ \hfill {\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}-{\left(\frac{𝑣}{𝑐}\right)}^2{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {\left(\frac{𝑣}{𝑐}\right)}^2\\ \hfill {\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {\left(\frac{𝑣}{𝑐}\right)}^2+{\left(\frac{𝑣}{𝑐}\right)}^2{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ \hfill {\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {\left(\frac{𝑣}{𝑐}\right)}^2(1+{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐})\\ \hfill {\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {\left(\frac{𝑣}{𝑐}\right)}^2{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ \hfill {𝑐}^2{\tanh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& {𝑣}^2\\ \hfill \pm 𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& 𝑣\end{array}$$ となるが、(102)式より ${{𝑢}_{\mathrm{(2)}}}^1$ と 𝑣 は同符号であることがわかるので、複号は負を採用し、 $$𝑣=-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\text{(103)}$$ である。(100)式の第0成分と(103)式を(101)式に代入すれば、(101)式も満たされていることがわかる。

アリスの速度 𝑣 が ${𝑡}_{\mathrm{(2)}}$ によらず一定であるから、アリスの位置 ${𝑥}_{\mathrm{(2)}}$ は座標時 ${𝑡}_{\mathrm{(2)}}$ の1次関数になるので(103)式の速度と(98)・(99)式の初期条件の座標を使って $$\begin{array}{lll}\hfill {𝑥}_{\mathrm{(2)}}& =& ({𝑡}_{\mathrm{(2)}}-\boxed{{𝑡}_{\mathrm{(2)}}\text{の初期値}})𝑣+\boxed{{𝑥}_{\mathrm{(2)}}\text{の初期値}}\\ & =& ({𝑡}_{\mathrm{(2)}}-\mathrm{𝑇₁})(-𝑐\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+(\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎})\\ & =& -𝑐({𝑡}_{\mathrm{(2)}}-\mathrm{𝑇₁})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}& \text{(104)}\end{array}$$ となる。また、アリスの固有時 𝜏_𝐴 も座標時 ${𝑡}_{\mathrm{(2)}}$ の1次関数になるので(98)・(100)式の初期条件を使って $$\begin{array}{lll}\hfill {𝜏}_{𝐴}& =& ({𝑡}_{\mathrm{(2)}}-\boxed{{𝑡}_{\mathrm{(2)}}\text{の初期値}})\frac{{\mathrm{d𝜏}}_{𝐴}}{{\mathrm{d𝑡}}_{\mathrm{(2)}}}+\boxed{{𝜏}_{𝐴}\text{の初期値}}\\ & =& ({𝑡}_{\mathrm{(2)}}-\boxed{{𝑡}_{\mathrm{(2)}}\text{の初期値}})\frac{𝑐}{{{𝑢}_{\mathrm{(2)}}}^0}+\boxed{{𝜏}_{𝐴}\text{の初期値}}& \text{←4元速度の定義}{{𝑢}_{\mathrm{(2)}}}^0=\frac{\mathrm{d}\left({\mathrm{𝑐𝑡}}_{\mathrm{(2)}}\right)}{{\mathrm{d𝜏}}_{𝐴}}=𝑐\frac{{\mathrm{d𝑡}}_{\mathrm{(2)}}}{{\mathrm{d𝜏}}_{𝐴}}\text{を使った。}\\ & =& ({𝑡}_{\mathrm{(2)}}-\mathrm{𝑇₁})\frac{𝑐}{𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& \frac{{𝑡}_{\mathrm{(2)}}-\mathrm{𝑇₁}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(105)}\end{array}$$ である。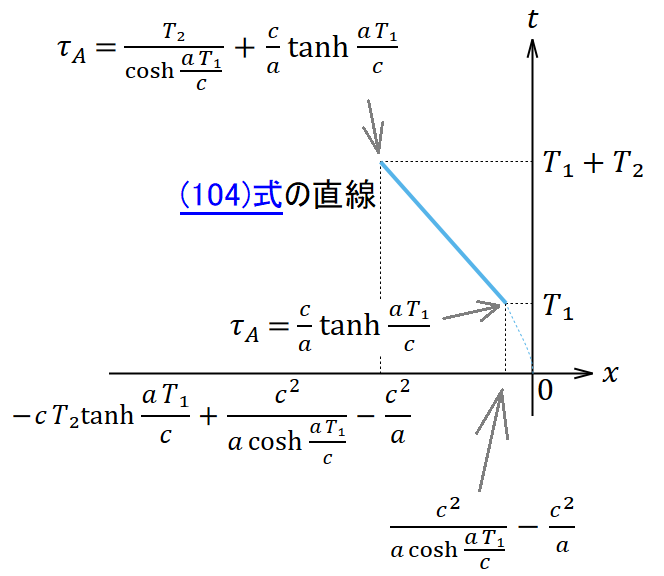ここで固有時 𝜏_𝐴 はスカラーだからその初期値は前節の最後で求めた値 $\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ をそのまま使った。以上でS₍₂₎系におけるアリスの世界線が(104)・(105)式のように求まった。

往路惰行局面の終了時では、 ${𝑡}_{\mathrm{(2)}}=\mathrm{𝑇₁}+\mathrm{𝑇₂}$ であるからこれを(104)・(105)式に代入すると、アリスの固有時は $\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$ 、位置は $-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}$ であり、4元速度は一定だから(100)式と同じで $(𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐},-𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐},0,0)$ である。

B.3. 折り返し局面

折り返し局面は $\mathrm{𝑇₁}+\mathrm{𝑇₂}\leqq {𝑡}_{\mathrm{(3)}}\leqq 3\mathrm{𝑇₁}+\mathrm{𝑇₂}$ である。ここで採用するS₍₃₎系は、空間原点に静止するボブが𝑥軸正方向に大きさ𝑎の一定の重力加速度を感じる座標系である。これは物理的な状況はB.1節の出発局面のリンドラー座標S₍₁₎系とまったく同じであり、ただ重力加速度の方向と人間が人為的に引いた座標系の 𝑥 軸の方向との関係が逆になっているだけである。ということはS₍₃₎系の計量や測地線の方程式は、S₍₁₎系のそれに対して 𝑥 軸の方向を逆にすればよい。

すなわちS₍₁₎系の計量テンソル(61)式の ${𝑥}_{\mathrm{(1)}}$ を $-{𝑥}_{\mathrm{(3)}}$ に置き換えることにより、S₍₃₎系の計量テンソルは $$\left({𝑔}_{𝜇𝜈}\right)=\left(\begin{array}{cccc}{𝑔}_{00}& {𝑔}_{01}& {𝑔}_{02}& {𝑔}_{03}\\ {𝑔}_{10}& {𝑔}_{11}& {𝑔}_{12}& {𝑔}_{13}\\ {𝑔}_{20}& {𝑔}_{21}& {𝑔}_{22}& {𝑔}_{23}\\ {𝑔}_{30}& {𝑔}_{31}& {𝑔}_{32}& {𝑔}_{33}\end{array}\right)=\left(\begin{array}{cccc}-{(-\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(3)}}+1)}^2& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\text{(106)}$$ のように求まる。また、S₍₁₎系の定義域は ${𝑥}_{\mathrm{(1)}}>-\frac{{𝑐}^2}{𝑎}$ であったから、これの ${𝑥}_{\mathrm{(1)}}$ を $-{𝑥}_{\mathrm{(3)}}$ に置き換えるとS₍₃₎系の定義域は $$\begin{array}{lll}\hfill -{𝑥}_{\mathrm{(3)}}& >& -\frac{{𝑐}^2}{𝑎}\\ \hfill {𝑥}_{\mathrm{(3)}}& <& \frac{{𝑐}^2}{𝑎}\end{array}$$ になる。

次に初期条件としてこの局面の開始時 ${𝑡}_{\mathrm{(3)}}=\mathrm{𝑇₁}+\mathrm{𝑇₂}$ におけるアリスの固有時と位置と4元速度を求める。これはB.2節の往路惰行局面の終了時 ${𝑡}_{\mathrm{(2)}}=\mathrm{𝑇₁}+\mathrm{𝑇₂}$ のS₍₂₎系における値をS₍₃₎系に座標変換したものである。固有時 𝜏_𝐴 はスカラーだから座標系に無関係なので初期条件は $${𝜏}_{𝐴}=\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\text{(107)}$$ である。位置と4元速度に関してはB.2節の最初のほうで述べたような理屈により、S₍₂₎系とS₍₃₎系が一致する ${𝑡}_{\mathrm{(2)}}={𝑡}_{\mathrm{(3)}}=\mathrm{𝑇₁}+\mathrm{𝑇₂}$ の瞬間に限り、4元速度の第0成分（𝑐𝑡 成分）を除いて座標変換しても値が変わらないから、初期条件は $$\begin{array}{llll}\hfill {𝑥}_{\mathrm{(3)}}& =& -𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}& \text{(108)}\\ \hfill {𝑦}_{\mathrm{(3)}}& =& 0& \text{(109)}\\ \hfill {𝑧}_{\mathrm{(3)}}& =& 0& \text{(110)}\\ \hfill {{𝑢}_{\mathrm{(3)}}}^1& =& -𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& \text{(111)}\\ \hfill {{𝑢}_{\mathrm{(3)}}}^2& =& 0& \text{(112)}\\ \hfill {{𝑢}_{\mathrm{(3)}}}^3& =& 0& \text{(113)}\end{array}$$ である。4元速度の第0成分（𝑐𝑡 成分）の初期条件は、それを使ってもこの後で独立でない条件式が増えるだけで何も変わらないので実は求める必要はないのであるが、気になる人のためにここで求めておく。4元速度の大きさの2乗がいつでも −𝑐² に等しいという条件を使うのである。

(106)式より 𝜇≠𝜈 のとき ${𝑔}_{𝜇𝜈}=0$であり、(112)・(113)式より ${{𝑢}_{\mathrm{(3)}}}^2={{𝑢}_{\mathrm{(3)}}}^3=0$ であるから、0でない項だけを残すと $$\begin{array}{lll}\hfill {𝑔}_{00}{{𝑢}_{\mathrm{(3)}}}^0{{𝑢}_{\mathrm{(3)}}}^0+{𝑔}_{11}{{𝑢}_{\mathrm{(3)}}}^1{{𝑢}_{\mathrm{(3)}}}^1& =& -{𝑐}^2\\ \hfill {𝑔}_{00}{\left({{𝑢}_{\mathrm{(3)}}}^0\right)}^2+{𝑔}_{11}{\left({{𝑢}_{\mathrm{(3)}}}^1\right)}^2& =& -{𝑐}^2\\ \hfill {𝑔}_{00}{\left({{𝑢}_{\mathrm{(3)}}}^0\right)}^2& =& -{𝑐}^2-{𝑔}_{11}{\left({{𝑢}_{\mathrm{(3)}}}^1\right)}^2\\ \hfill {\left({{𝑢}_{\mathrm{(3)}}}^0\right)}^2& =& \frac{-{𝑐}^2-{𝑔}_{11}{\left({{𝑢}_{\mathrm{(3)}}}^1\right)}^2}{{𝑔}_{00}}\\ \hfill {{𝑢}_{\mathrm{(3)}}}^0& =& \pm \sqrt{\frac{-{𝑐}^2-{𝑔}_{11}{\left({{𝑢}_{\mathrm{(3)}}}^1\right)}^2}{{𝑔}_{00}}}\\ & =& \pm \sqrt{\frac{-{𝑐}^2-1{(-𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}{-{(-\frac{𝑎}{{𝑐}^2}{𝑥}_{\mathrm{(3)}}+1)}^2}}& \text{←}\text{(106)}\text{・}\text{(111)式}\text{を代入した。}\\ & =& \pm \sqrt{\frac{-{𝑐}^2-{𝑐}^2{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{-{\{-\frac{𝑎}{{𝑐}^2}(-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎})+1\}}^2}}& \text{←}\text{(108)式}\text{を代入した。}\\ & =& \pm \sqrt{\frac{-{𝑐}^2(1+{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐})}{-{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+1+1)}^2}}\\ & =& \pm \sqrt{\frac{{𝑐}^2{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+2)}^2}}\\ & =& \pm \frac{𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+2}\end{array}$$ であるが、 𝜏_𝐴 が増えるとき ${𝑡}_{\mathrm{(3)}}$ も増えてほしいので複号は正を採用し、 $${{𝑢}_{\mathrm{(3)}}}^0=\frac{𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+2}\text{(114)}$$ である。

次にアリスの運動方程式を求める。この節の最初の方で述べたように、A.1節の出発局面のS₍₁₎系における解に対して 𝑥 軸の方向を逆にすればよい。さらに(109)・(110)式より初期条件の第2・3成分（𝑦, 𝑧 成分）が0である点も同じであるから、それを適用した後の(80)〜(83)式（𝜏_𝐴 によるパラメータ表示）または(85)・(86)・(88)・(89)式（${𝑡}_{\mathrm{(1)}}$ の関数としての表示）に対して次のような置き換えをすればよい。

第2・3成分（𝑦, 𝑧 成分）はずっと0であるからこの節ではもう書かない。 𝜏_𝐴 によるパラメータ表示である(80)〜(83)式に対して(115)式の置き換えをすると、 $$\begin{array}{ll}{\mathrm{𝑐𝑡}}_{\mathrm{(3)}}=\frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{{𝑐}^4({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}{𝑎\mathrm{𝐾₁₀}}+\mathrm{𝐾₁₂}& \text{(116)}\\ {𝑥}_{\mathrm{(3)}}=\frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2{({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}^2+\frac{{𝑎}^2{\mathrm{𝐾₁₀}}^2}{{𝑐}^6}}& \text{(117)}\\ {{𝑢}_{\mathrm{(3)}}}^0=\frac{\mathrm{𝐾₁₀}}{-{𝑐}^2{({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}^2+\frac{{𝑎}^2{\mathrm{𝐾₁₀}}^2}{{𝑐}^6}}=\frac{\mathrm{𝐾₁₀}}{{(-{𝑥}_{\mathrm{(3)}}+\frac{{𝑐}^2}{𝑎})}^2}& \text{(118)}\\ {{𝑢}_{\mathrm{(3)}}}^1=\frac{{𝑐}^2({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}{\sqrt{-{𝑐}^2{({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}^2+\frac{{𝑎}^2{\mathrm{𝐾₁₀}}^2}{{𝑐}^6}}}=\frac{{𝑐}^2({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}{-{𝑥}_{\mathrm{(3)}}+\frac{{𝑐}^2}{𝑎}}& \text{(119)}\end{array}$$ である。(85)・(86)・(88)・(89)式（${𝑡}_{\mathrm{(1)}}$ の関数としての表示）に対して(115)式の置き換えをすると、 $$\begin{array}{ll}{𝜏}_{𝐴}=\frac{𝑎\mathrm{𝐾₁₀}}{{𝑐}^4}\tanh \left\{\frac{𝑎}{𝑐}\right({𝑡}_{\mathrm{(3)}}-\frac{\mathrm{𝐾₁₂}}{𝑐}\left)\right\}-\mathrm{𝐾₁₁}& \text{(120)}\\ {𝑥}_{\mathrm{(3)}}=\frac{{𝑐}^2}{𝑎}-\frac{𝑎\left|\mathrm{𝐾₁₀}\right|}{{𝑐}^3\cosh \left\{\frac{𝑎}{𝑐}\right({𝑡}_{\mathrm{(3)}}-\frac{\mathrm{𝐾₁₂}}{𝑐}\left)\right\}}& \text{(121)}\\ {{𝑢}_{\mathrm{(3)}}}^0=\frac{{𝑐}^6{\cosh }^2\left\{\frac{𝑎}{𝑐}\right({𝑡}_{\mathrm{(3)}}-\frac{\mathrm{𝐾₁₂}}{𝑐}\left)\right\}}{{𝑎}^2\mathrm{𝐾₁₀}}& \text{(122)}\\ {{𝑢}_{\mathrm{(3)}}}^1=\frac{\mathrm{𝐾₁₀}}{\left|\mathrm{𝐾₁₀}\right|}𝑐\sinh \left\{\frac{𝑎}{𝑐}\right({𝑡}_{\mathrm{(3)}}-\frac{\mathrm{𝐾₁₂}}{𝑐}\left)\right\}& \text{(123)}\end{array}$$ である。積分定数を定めるためには前者の組と後者の組のどちらを使っても（あるいは両方を少しずつ使っても）構わないが、ここでは計算が楽そうな前者の(116)〜(119)式を使う。(119)式の左辺と右辺に初期条件(111)・(107)・(108)式を代入すると、 $$\begin{array}{llll}\hfill {{𝑢}_{\mathrm{(3)}}}^1& =& \frac{{𝑐}^2({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}{-{𝑥}_{\mathrm{(3)}}+\frac{{𝑐}^2}{𝑎}}& \text{←}\text{(119)式}\\ \hfill -𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{{𝑐}^2\left\{\right(\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+\mathrm{𝐾₁₁}\}}{-(-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎})+\frac{{𝑐}^2}{𝑎}}& \text{←}\text{(111)}\text{・}\text{(107)}\text{・}\text{(108)式}\text{を代入した。}\\ \hfill -𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{{𝑐}^2(\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₁₁})}{𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{2{𝑐}^2}{𝑎}}\\ \hfill \frac{-𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}(𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{2{𝑐}^2}{𝑎})}{{𝑐}^2}& =& \frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₁₁}\\ \hfill -\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝐾₁₁}\\ \hfill -\mathrm{𝑇₂}\frac{\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₁₁}\\ \hfill -\mathrm{𝑇₂}\frac{{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}+1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₁₁}\\ \hfill -\mathrm{𝑇₂}\frac{{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₁₁}\\ \hfill -\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}& =& \mathrm{𝐾₁₁}& \text{(124)}\end{array}$$ のように𝐾₁₁が定まる。(118)式の左辺と右辺に初期条件(114)・(108)式を代入すると、 $$\begin{array}{llll}\hfill {{𝑢}_{\mathrm{(3)}}}^0& =& \frac{\mathrm{𝐾₁₀}}{{(-{𝑥}_{\mathrm{(3)}}+\frac{{𝑐}^2}{𝑎})}^2}& \text{←}\text{(118)式}\\ \hfill \frac{𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+2}& =& \frac{\mathrm{𝐾₁₀}}{{\{-(-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎})+\frac{{𝑐}^2}{𝑎}\}}^2}& \text{←}\text{(114)}\text{・}\text{(108)式}\text{を代入した。}\\ \hfill \frac{𝑐\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎}{{𝑐}^2}(𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{2{𝑐}^2}{𝑎})}& =& \frac{\mathrm{𝐾₁₀}}{{(𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{2{𝑐}^2}{𝑎})}^2}\\ \hfill \frac{{𝑐}^3}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}(𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{2{𝑐}^2}{𝑎})& =& \mathrm{𝐾₁₀}\\ \hfill \frac{{𝑐}^5}{{𝑎}^2}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})& =& \mathrm{𝐾₁₀}& \text{(125)}\end{array}$$ のように𝐾₁₀が定まる。今定めた(124)・(125)式の𝐾₁₁と𝐾₁₀が(117)式を満たすかどうか確認すると、 $$\begin{array}{lll}\hfill \text{(117)式の左辺}& =& {𝑥}_{\mathrm{(3)}}\\ & =& -𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}& \text{←}\text{(108)式}\text{を代入した。}\\ \hfill \text{(117)式の右辺}& =& \frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2{({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}^2+\frac{{𝑎}^2{\mathrm{𝐾₁₀}}^2}{{𝑐}^6}}\\ & =& \frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2{\left\{\right(\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+(-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2𝑐}{𝑎}𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}^2+\frac{{𝑎}^2{\left\{\frac{{𝑐}^5}{{𝑎}^2}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\right\}}^2}{{𝑐}^6}}& \text{←}\text{(107)}\text{・}\text{(124)}\text{・}\text{(125)式}\text{を代入した。}\\ & =& \frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2{\{\mathrm{𝑇₂}\frac{1-{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}^2+\frac{{𝑎}^2\frac{{𝑐}^{10}}{{𝑎}^4}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}{{𝑐}^6}}\\ & =& \frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2{\{\mathrm{𝑇₂}\frac{-{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}^2+\frac{{𝑐}^4}{{𝑎}^2}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\sqrt{-{𝑐}^2\frac{{𝑐}^2}{{𝑎}^2}{\{-\frac{𝑎\mathrm{𝑇₂}}{𝑐}\frac{{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}^2+\frac{{𝑐}^4}{{𝑎}^2}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\sqrt{-\frac{{𝑐}^4}{{𝑎}^2}{\{-\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}(1-2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\}}^2+\frac{{𝑐}^4}{{𝑎}^2}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\sqrt{-{{\tanh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}\{-\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+(1-2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\}}^2+{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\sqrt{-{\tanh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2+{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\sqrt{(-{\tanh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}+1){(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\sqrt{\frac{1}{{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}^2}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\\ & =& \frac{{𝑐}^2}{𝑎}-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{2{𝑐}^2}{𝑎}\\ & =& -𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}\end{array}$$ となって左辺と右辺が同じになるので確かに(117)式も満たされている。(118)・(119)式のそれぞれ右の等号は(117)式と同じことを言っているのだから、考えてみれば当たり前だ。少し上で4元速度の第0成分の初期条件を使う必要がないと言ったのはこのことである。

最後に残った𝐾₁₂を定めるため(116)式に初期条件(107)式と ${𝑡}_{\mathrm{(3)}}=\mathrm{𝑇₁}+\mathrm{𝑇₂}$ および(124)・(125)式を代入すると、 $$\begin{array}{llll}\hfill {\mathrm{𝑐𝑡}}_{\mathrm{(3)}}& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{{𝑐}^4({𝜏}_{𝐴}+\mathrm{𝐾₁₁})}{𝑎\mathrm{𝐾₁₀}}+\mathrm{𝐾₁₂}& \text{←}\text{(116)式}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{{𝑐}^4\left\{\right(\frac{\mathrm{𝑇₂}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+(-\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}{𝑎\frac{{𝑐}^5}{{𝑎}^2}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}+\mathrm{𝐾₁₂}& \text{←}{𝑡}_{\mathrm{(3)}}\text{の初期条件と}\text{(107)}\text{・}\text{(124)}\text{・}\text{(125)式}\text{を代入した。}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{{𝑐}^4\{\mathrm{𝑇₂}\frac{1-{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}{\frac{{𝑐}^5}{𝑎}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{𝑎\{\mathrm{𝑇₂}\frac{-{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\frac{𝑐}{𝑎}(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}{𝑐(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{𝑎\frac{𝑐}{𝑎}\{-\frac{𝑎\mathrm{𝑇₂}}{𝑐}\frac{{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+(\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}}{𝑐(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{-\frac{𝑎\mathrm{𝑇₂}}{𝑐}\frac{{\sinh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-2\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\frac{-\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}(-\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐})+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}\mathrm{artanh}\left\{\tanh \right(-\frac{𝑎\mathrm{𝑇₁}}{𝑐}\left)\right\}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \frac{{𝑐}^2}{𝑎}(-\frac{𝑎\mathrm{𝑇₁}}{𝑐})+\mathrm{𝐾₁₂}\\ \hfill 𝑐(\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& -𝑐\mathrm{𝑇₁}+\mathrm{𝐾₁₂}\\ \hfill 𝑐(2\mathrm{𝑇₁}+\mathrm{𝑇₂})& =& \mathrm{𝐾₁₂}& \text{(126)}\end{array}$$ のように𝐾₁₂が定まる。

(124)〜(126)式で定まった積分定数の値を(120)〜(123)式に代入すれば、S₍₃₎系で見たアリスの固有時と位置と4元速度は次のようになる。

だんだん式が長くなってきたが、大部分は定数であって変数は ${𝑡}_{\mathrm{(3)}}$ だけなので、それほどややこしい関数ではない。

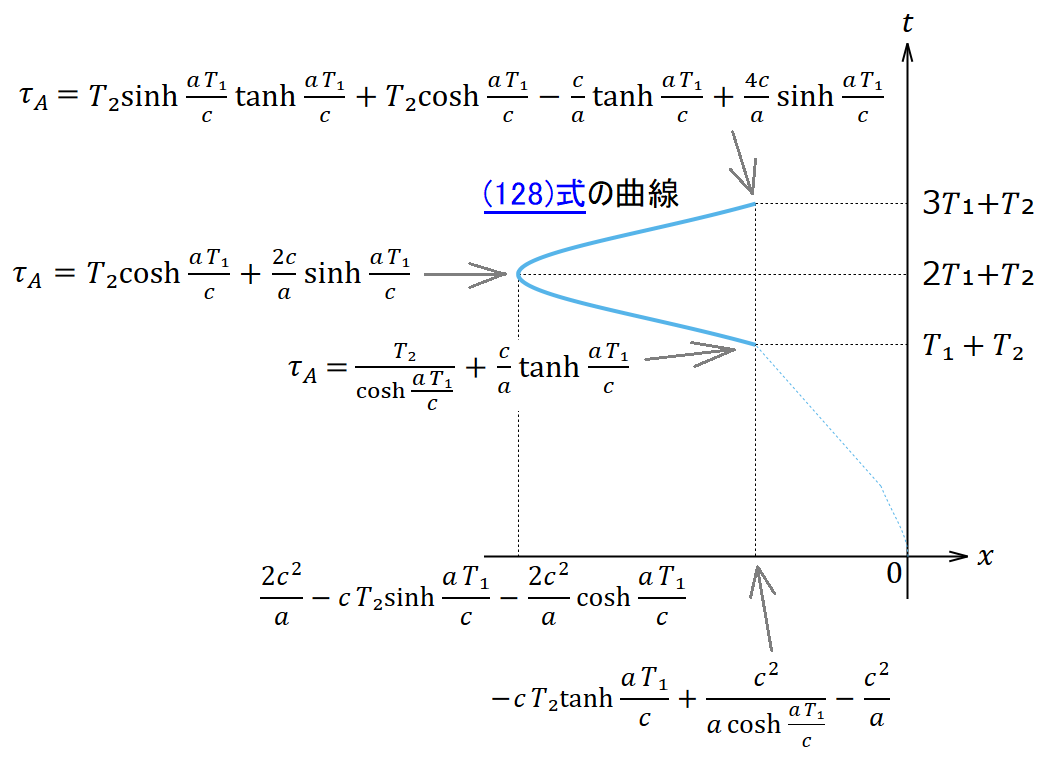
ボブの固有時が ${𝜏}_{𝐵}={𝑡}_{\mathrm{(3)}}=2\mathrm{𝑇₁}+\mathrm{𝑇₂}$ であるときに往路から復路に切り替わることが期待される。(130)式に ${𝑡}_{\mathrm{(3)}}=2\mathrm{𝑇₁}+\mathrm{𝑇₂}$ を代入するとアリスの4元速度の第1成分（𝑥 成分）は 0 となり、この瞬間に負から正に変わることがわかる。このとき、(128)式よりアリスの位置は $$\begin{array}{lll}\hfill {𝑥}_{\mathrm{(3)}}& =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\cdot \frac{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\left\{\right(2\mathrm{𝑇₁}+\mathrm{𝑇₂})-2\mathrm{𝑇₁}-\mathrm{𝑇₂}\}}{𝑐}}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\\ & =& \frac{{𝑐}^2}{𝑎}-𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎}-\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& \frac{2{𝑐}^2}{𝑎}-𝑐\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{2{𝑐}^2}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\end{array}$$ である。この位置はアリスがボブから最も遠くに離れたときの位置である。またこのときのアリスの経過時間は(127)式に ${𝑡}_{\mathrm{(3)}}=2\mathrm{𝑇₁}+\mathrm{𝑇₂}$ を代入すると $${𝜏}_{𝐴}=\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}$$ である。

折り返し局面の終了時では、 ${𝑡}_{\mathrm{(3)}}=3\mathrm{𝑇₁}+\mathrm{𝑇₂}$ であるからこれを(127)〜(130)式に代入すると、アリスの固有時は $$\begin{array}{lll}\hfill {𝜏}_{𝐴}& =& (\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{𝑐}{𝑎}+\frac{2𝑐}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\left\{\right(3\mathrm{𝑇₁}+\mathrm{𝑇₂})-2\mathrm{𝑇₁}-\mathrm{𝑇₂}\}}{𝑐}+\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& (\mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{𝑐}{𝑎}+\frac{2𝑐}{𝑎}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐})\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& \mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{2𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\\ & =& \mathrm{𝑇₂}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\mathrm{𝑇₂}\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{𝑐}{𝑎}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{4𝑐}{𝑎}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}\end{array}$$ であり、位置は $$\begin{array}{lll}\hfill {𝑥}_{\mathrm{(3)}}& =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\cdot \frac{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎({𝑡}_{\mathrm{(3)}}-2\mathrm{𝑇₁}-\mathrm{𝑇₂})}{𝑐}}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\cdot \frac{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\left\{\right(3\mathrm{𝑇₁}+\mathrm{𝑇₂})-2\mathrm{𝑇₁}-\mathrm{𝑇₂}\}}{𝑐}}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}\cdot \frac{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}\\ & =& \frac{{𝑐}^2}{𝑎}-\frac{{𝑐}^2}{𝑎}(\frac{𝑎\mathrm{𝑇₂}}{𝑐}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-\frac{1}{\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}+2)\\ & =& \frac{{𝑐}^2}{𝑎}-𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{2{𝑐}^2}{𝑎}\\ & =& -𝑐\mathrm{𝑇₂}\tanh \frac{𝑎\mathrm{𝑇₁}}{𝑐}+\frac{{𝑐}^2}{𝑎\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}}-\frac{{𝑐}^2}{𝑎}\end{array}$$ であり、4元速度は $(\frac{𝑐{\cosh }^2\frac{𝑎\mathrm{𝑇₁}}{𝑐}}{\frac{𝑎\mathrm{𝑇₂}}{𝑐}\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐}-1+2\cosh \frac{𝑎\mathrm{𝑇₁}}{𝑐}},𝑐\sinh \frac{𝑎\mathrm{𝑇₁}}{𝑐},0,0)$ である。