「双子のパラドックス」を両者の視点から計算する。(6)

B.4. 復路惰行局面

復路路惰行局面は $3 𝑇₁ + 𝑇₂ ≦ 𝑡_{(4)} ≦ 3 𝑇₁ + 2 𝑇₂$ である。ここで採用するS₍₄₎系は慣性系のミンコフスキー座標である。アリスには何の力も作用しないから、この座標系でアリスの運動はただの直線である。初期条件を当てはめればその直線は一意に決まる。初期条件として、この局面の開始時のアリスの固有時と位置と4元速度を使えばよい。

この局面の開始時は折り返し局面の終了時と同じである。その際、B.2節の最初のほうで述べたような理屈により、固有時と位置 $𝑥_{(3)}$ と4元速度の空間成分 ${𝑢_{(3)}}^{1}$ は折り返し局面のS₍₃₎系での値と同じものをそのまま使えばよい。したがってB.3節の最後で計算したように固有時は $𝜏_{𝐴} = 𝑇₂ \sinh \frac{𝑎 𝑇₁}{𝑐} \tanh \frac{𝑎 𝑇₁}{𝑐} + 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} (131)$ であり、位置は $𝑥_{(4)} = - 𝑐 𝑇₂ \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎} (132)$ であり、4元速度の第1成分（𝑥 成分）は ${𝑢_{(4)}}^{1} = 𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐} (133)$ である。第2・3成分（𝑦, 𝑧 成分）はここでもずっと0なのでもう書かない。普通の3次元的な速度 𝑣 は、(102)式から(103)式を導出したときと同様でただ符号が異なるだけなので、 $𝑣 = 𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐} (134)$ である。この 𝑣 は局面を通して一定であるから、座標時 $𝑡_{(4)}$ とアリスの固有時 𝜏_𝐴 との関係は(3)式の公式より $\begin{array}{l} \frac{{d𝜏}_{𝐴}}{{d𝑡}_{(4)}} & = & \sqrt{1 - {(\frac{𝑣}{𝑐})}^{2}} \\ = & \sqrt{1 - {(\frac{𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}}{𝑐})}^{2}} \\ = & \sqrt{1 - \tanh^{2} \frac{𝑎 𝑇₁}{𝑐}} \\ = & \sqrt{\frac{1}{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}} \\ = & \frac{1}{\cosh \frac{𝑎 𝑇₁}{𝑐}} & (135) \end{array}$ である。

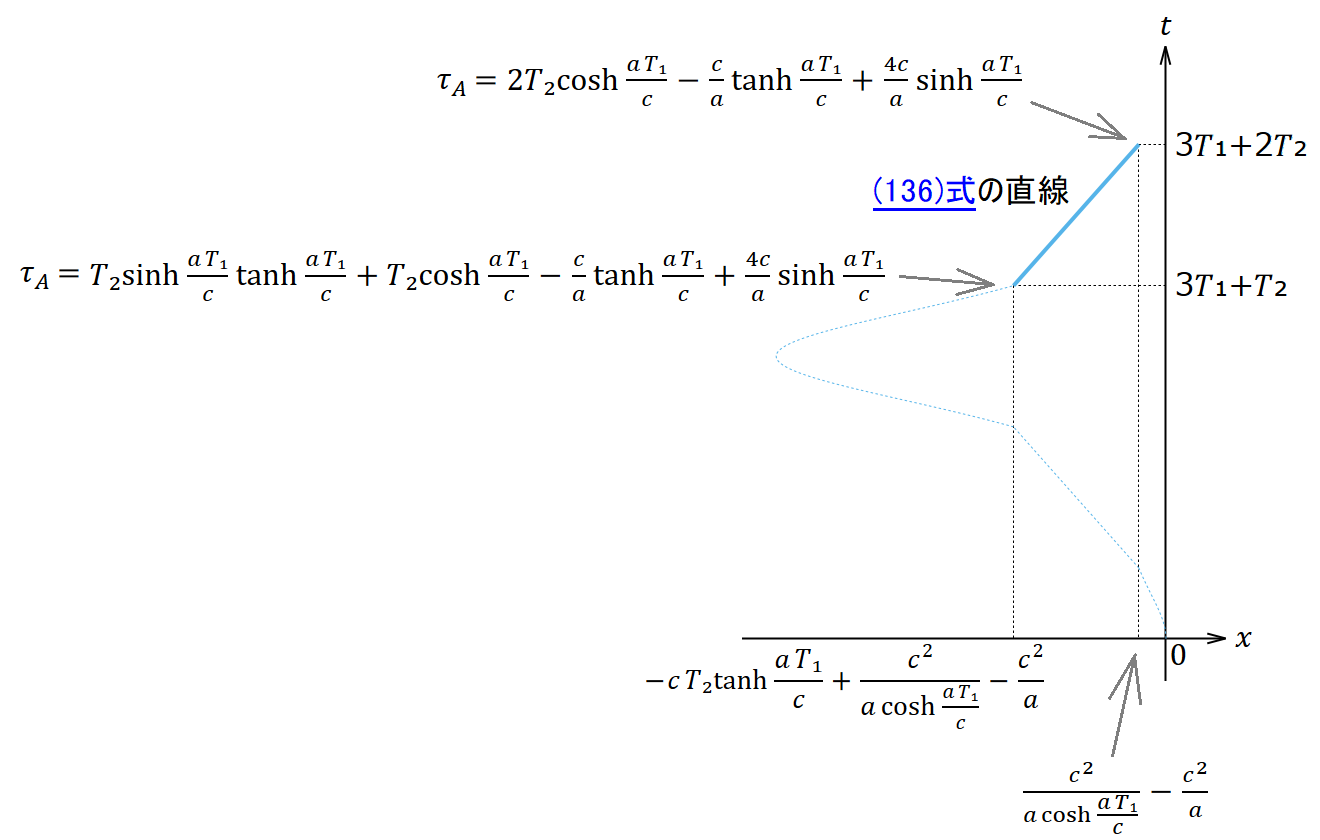
アリスの速度 𝑣 が $𝑡_{(4)}$ によらず一定であるから、アリスの位置 $𝑥_{(4)}$ は座標時 $𝑡_{(4)}$ の1次関数になるので(134)式の速度と(131)・(132)式の初期条件の座標を使って $\begin{array}{l} 𝑥_{(4)} & = & (𝑡_{(4)} - 𝑡_{(4)} の初期値) 𝑣 + 𝑥_{(4)} の初期値 \\ = & {𝑡_{(4)} - (3 𝑇₁ + 𝑇₂)} (𝑐 \tanh \frac{𝑎 𝑇₁}{𝑐}) + (- 𝑐 𝑇₂ \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎}) \\ = & 𝑐 (𝑡_{(4)} - 3 𝑇₁ - 𝑇₂) \tanh \frac{𝑎 𝑇₁}{𝑐} - 𝑐 𝑇₂ \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎} \\ = & 𝑐 (𝑡_{(4)} - 3 𝑇₁ - 2 𝑇₂) \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎} & (136) \end{array}$ となる。また、アリスの固有時 𝜏_𝐴 も座標時 $𝑡_{(4)}$ の1次関数になるので(131)式の初期条件と(135)式を使って $\begin{array}{l} 𝜏_{𝐴} & = & (𝑡_{(4)} - 𝑡_{(4)} の初期値) \frac{{d𝜏}_{𝐴}}{{d𝑡}_{(4)}} + 𝜏_{𝐴} の初期値 \\ = & {𝑡_{(4)} - (3 𝑇₁ + 𝑇₂)} \frac{1}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + (𝑇₂ \sinh \frac{𝑎 𝑇₁}{𝑐} \tanh \frac{𝑎 𝑇₁}{𝑐} + 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) \\ = & \frac{𝑡_{(4)} - 3 𝑇₁ - 𝑇₂}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₂ \sinh \frac{𝑎 𝑇₁}{𝑐} \tanh \frac{𝑎 𝑇₁}{𝑐} + 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & \frac{𝑡_{(4)} - 3 𝑇₁ - 𝑇₂}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₂ \frac{\sinh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} + 𝑇₂ \frac{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & \frac{𝑡_{(4)} - 3 𝑇₁ + 𝑇₂ (- 1 + \sinh^{2} \frac{𝑎 𝑇₁}{𝑐} + \cosh^{2} \frac{𝑎 𝑇₁}{𝑐})}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & \frac{𝑡_{(4)} - 3 𝑇₁ + 2 𝑇₂ \sinh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} & (137) \end{array}$ である。

復路惰行局面の終了時では、 $𝑡_{(4)} = 3 𝑇₁ + 2 𝑇₂$ であるからこれを(137)・(136)式に代入すると、アリスの固有時は $\begin{array}{l} 𝜏_{𝐴} & = & \frac{(3 𝑇₁ + 2 𝑇₂) - 3 𝑇₁ + 2 𝑇₂ \sinh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & \frac{2 𝑇₂ (1 + \sinh^{2} \frac{𝑎 𝑇₁}{𝑐})}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & \frac{2 𝑇₂ \cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \\ = & 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} \end{array}$ であり、位置は $\frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎}$ であり、4元速度は一定だからその第1成分（𝑥 成分）は(133)式と同じで $𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐}$ である。

B.5. 帰還局面

帰還局面は $3 𝑇₁ + 2 𝑇₂ ≦ 𝑡_{(5)} ≦ 4 𝑇₁ + 2 𝑇₂$ である。ここで採用するS₍₅₎系は、空間原点に静止するボブが𝑥軸負方向に大きさ𝑎の一定の重力加速度を感じる座標系である。これは物理的な状況はB.1節の出発局面のリンドラー座標S₍₁₎系とまったく同じであり、座標の取り方もまったく同じである。したがってS₍₅₎系の計量や測地線の方程式は、S₍₁₎系と同じ式を使えばよい。なお、このことはS₍₁₎系とS₍₅₎系が同一の座標系だと言っているわけではない。異なる座標系であるが座標の値に依存する性質がまったく同じなだけである。

この局面の開始時は復路惰行局面の終了時と同じである。初期条件としてこの局面の開始時 $𝑡_{(5)} = 3 𝑇₁ + 2 𝑇₂$ におけるアリスの固有時と位置と4元速度を求める。これはB.4節の復路惰行局面の終了時 $𝑡_{(4)} = 3 𝑇₁ + 2 𝑇₂$ のS₍₄₎系における値をS₍₅₎系に座標変換したものである。その際、B.2節の最初のほうで述べたような理屈により、固有時と位置 $𝑥_{(5)}$ と4元速度の空間成分 ${𝑢_{(5)}}^{1}$ は復路惰行局面のS₍₄₎系での値と同じものをそのまま使えばよい。したがってB.4節の最後で計算したように固有時は $𝜏_{𝐴} = 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} (138)$ であり、位置は $𝑥_{(5)} = \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎} (139)$ であり、4元速度の第1成分（𝑥 成分）は ${𝑢_{(5)}}^{1} = 𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐} (140)$ である。B.3節で述べたように、4元速度の第0成分（𝑐𝑡 成分）の初期条件は冗長であり新たな条件が追加されるわけではないのでそれはもう求めない。

次にアリスの運動方程式を求める。それはA.1節の出発局面のS₍₁₎系における解と同じ式を使えばよい。さらに初期条件の第2・3成分（𝑦, 𝑧 成分）が0である点も同じであるから、それを適用した後の(80)〜(83)式（𝜏_𝐴 によるパラメータ表示）または(85)・(86)・(88)・(89)式（ $𝑡_{(1)}$ の関数としての表示）に対して次のような置き換えをすればよい。

{\begin{cases} 𝑡_{(1)} & \to & 𝑡_{(5)} \\ 𝑥_{(1)} & \to & 𝑥_{(5)} \\ {𝑢_{(1)}}^{0} & \to & {𝑢_{(5)}}^{0} \\ {𝑢_{(1)}}^{1} & \to & {𝑢_{(5)}}^{1} \end{cases} (141)

𝜏_𝐴 によるパラメータ表示である(80)〜(83)式に対して(141)式の置き換えをすると、 $\begin{array}{l} {𝑐𝑡}_{(5)} = \frac{𝑐^{2}}{𝑎} artanh \frac{𝑐^{4} (𝜏_{𝐴} + 𝐾₁₁)}{𝑎 𝐾₁₀} + 𝐾₁₂ & (142) \\ 𝑥_{(5)} = - \frac{𝑐^{2}}{𝑎} + \sqrt{- 𝑐^{2} {(𝜏_{𝐴} + 𝐾₁₁)}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} & (143) \\ {𝑢_{(5)}}^{0} = \frac{𝐾₁₀}{- 𝑐^{2} {(𝜏_{𝐴} + 𝐾₁₁)}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} = \frac{𝐾₁₀}{{(𝑥_{(5)} + \frac{𝑐^{2}}{𝑎})}^{2}} & (144) \\ {𝑢_{(5)}}^{1} = - \frac{𝑐^{2} (𝜏_{𝐴} + 𝐾₁₁)}{\sqrt{- 𝑐^{2} {(𝜏_{𝐴} + 𝐾₁₁)}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}}} = - \frac{𝑐^{2} (𝜏_{𝐴} + 𝐾₁₁)}{𝑥_{(5)} + \frac{𝑐^{2}}{𝑎}} & (145) \end{array}$ である。(85)・(86)・(88)・(89)式（ $𝑡_{(1)}$ の関数としての表示）に対して(141)式の置き換えをすると、 $\begin{array}{l} 𝜏_{𝐴} = \frac{𝑎 𝐾₁₀}{𝑐^{4}} \tanh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})} - 𝐾₁₁ & (146) \\ 𝑥_{(5)} = - \frac{𝑐^{2}}{𝑎} + \frac{𝑎 | 𝐾₁₀ |}{𝑐^{3} \cosh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})}} & (147) \\ {𝑢_{(5)}}^{0} = \frac{𝑐^{6} \cosh^{2} {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})}}{𝑎^{2} 𝐾₁₀} & (148) \\ {𝑢_{(5)}}^{1} = - \frac{𝐾₁₀}{| 𝐾₁₀ |} 𝑐 \sinh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})} & (149) \end{array}$ である。積分定数を定めるためには前者の組と後者の組のどちらを使っても（あるいは両方を少しずつ使っても）構わないが、ここでは計算が楽そうな前者の(142)〜(145)式を使う。(145)式の左辺と右辺に初期条件(138)〜(140)式を代入すると、 $\begin{array}{l} {𝑢_{(5)}}^{1} & = & - \frac{𝑐^{2} (𝜏_{𝐴} + 𝐾₁₁)}{𝑥_{(5)} + \frac{𝑐^{2}}{𝑎}} & ← (145)式 \\ 𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐} & = & - \frac{𝑐^{2} {(2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) + 𝐾₁₁}}{(\frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎}) + \frac{𝑐^{2}}{𝑎}} & ← (138) 〜 (140)式を代入した。 \\ 𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐} & = & - \frac{𝑐^{2} (2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} + 𝐾₁₁)}{(\frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}})} \\ \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} 𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐} & = & - 𝑐^{2} (2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} + 𝐾₁₁) \\ \frac{𝑐 \sinh \frac{𝑎 𝑇₁}{𝑐}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} & = & - (2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} + 𝐾₁₁) \\ \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} & = & - 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} - \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} - 𝐾₁₁ \\ 𝐾₁₁ & = & - 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} & (150) \end{array}$ のように𝐾₁₁が定まる。(143)式の左辺と右辺に初期条件(138)・(139)式および(150)式を代入すると、 $\begin{array}{l} 𝑥_{(5)} & = & - \frac{𝑐^{2}}{𝑎} + \sqrt{- 𝑐^{2} {(𝜏_{𝐴} + 𝐾₁₁)}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} & ← (143)式 \\ \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} - \frac{𝑐^{2}}{𝑎} & = & - \frac{𝑐^{2}}{𝑎} + \sqrt{- 𝑐^{2} {(2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) + (- 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐})}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} & ← (138) ・ (139) ・ (150)式を代入した。 \\ \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} & = & \sqrt{- 𝑐^{2} {(- \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐})}^{2} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} \\ \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 𝑇₁}{𝑐}} & = & \sqrt{- \frac{𝑐^{4}}{𝑎^{2}} \tanh^{2} \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}}} \\ \frac{𝑐^{4}}{𝑎^{2} \cosh^{2} \frac{𝑎 𝑇₁}{𝑐}} & = & - \frac{𝑐^{4}}{𝑎^{2}} \tanh^{2} \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}} \\ \frac{𝑐^{4}}{𝑎^{2}} \tanh^{2} \frac{𝑎 𝑇₁}{𝑐} + \frac{𝑐^{4}}{𝑎^{2} \cosh^{2} \frac{𝑎 𝑇₁}{𝑐}} & = & \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}} \\ \frac{𝑐^{4}}{𝑎^{2}} (\frac{\sinh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}} + \frac{1}{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}) & = & \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}} \\ \frac{𝑐^{4}}{𝑎^{2}} \frac{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}}{\cosh^{2} \frac{𝑎 𝑇₁}{𝑐}} & = & \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}} \\ \frac{𝑐^{4}}{𝑎^{2}} & = & \frac{𝑎^{2} {𝐾₁₀}^{2}}{𝑐^{6}} \\ \frac{𝑐^{10}}{𝑎^{4}} & = & {𝐾₁₀}^{2} \\ \pm \frac{𝑐^{5}}{𝑎^{2}} & = & 𝐾₁₀ \end{array}$ であるが、(144)式より ${𝑢_{(5)}}^{0}$ と𝐾₁₀の符号が同じであり、 𝜏_𝐴 が増えるとき $𝑡_{(5)}$ も増えてほしいので ${𝑢_{(5)}}^{0} > 0$ だから、複号は正を採用し、 $𝐾₁₀ = \frac{𝑐^{5}}{𝑎^{2}} (151)$ のように𝐾₁₀が定まる。(142)式に初期条件(138)式と $𝑡_{(5)} = 3 𝑇₁ + 2 𝑇₂$ および(150)・(151)式を代入すると、 $\begin{array}{l} {𝑐𝑡}_{(5)} & = & \frac{𝑐^{2}}{𝑎} artanh \frac{𝑐^{4} (𝜏_{𝐴} + 𝐾₁₁)}{𝑎 𝐾₁₀} + 𝐾₁₂ \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & \frac{𝑐^{2}}{𝑎} artanh \frac{𝑐^{4} {(2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) + (- 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐})}}{𝑎 \frac{𝑐^{5}}{𝑎^{2}}} + 𝐾₁₂ & ← 𝑡_{(5)} の初期条件と (138) ・ (150) ・ (151)式を代入した。 \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & \frac{𝑐^{2}}{𝑎} artanh \frac{𝑐^{4} (- \frac{𝑐}{𝑎} \tanh \frac{𝑎 𝑇₁}{𝑐})}{(\frac{𝑐^{5}}{𝑎})} + 𝐾₁₂ \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & \frac{𝑐^{2}}{𝑎} artanh (- \tanh \frac{𝑎 𝑇₁}{𝑐}) + 𝐾₁₂ \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & \frac{𝑐^{2}}{𝑎} artanh {\tanh (- \frac{𝑎 𝑇₁}{𝑐})} + 𝐾₁₂ \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & \frac{𝑐^{2}}{𝑎} (- \frac{𝑎 𝑇₁}{𝑐}) + 𝐾₁₂ \\ 𝑐 (3 𝑇₁ + 2 𝑇₂) & = & - 𝑐 𝑇₁ + 𝐾₁₂ \\ 𝑐 (4 𝑇₁ + 2 𝑇₂) & = & 𝐾₁₂ & (152) \end{array}$ のように𝐾₁₂が定まる。

(150)〜(152)式で定まった積分定数の値を(146)〜(149)式に代入すれば、S₍₅₎系で見たアリスの固有時と位置と4元速度は次のようになる。

\begin{array}{l} 𝜏_{𝐴} & = & \frac{𝑎 𝐾₁₀}{𝑐^{4}} \tanh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})} - 𝐾₁₁ & ← (146)式 \\ = & \frac{𝑎 \frac{𝑐^{5}}{𝑎^{2}}}{𝑐^{4}} \tanh [\frac{𝑎}{𝑐} {𝑡_{(5)} - \frac{𝑐 (4 𝑇₁ + 2 𝑇₂)}{𝑐}}] - (- 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} - \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}) & ←積分定数の値を代入した。 \\ = & \frac{𝑐}{𝑎} \tanh \frac{𝑎 (𝑡_{(5)} - 4 𝑇₁ - 2 𝑇₂)}{𝑐} + 2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐} & (153) \\ 𝑥_{(5)} & = & - \frac{𝑐^{2}}{𝑎} + \frac{𝑎 | 𝐾₁₀ |}{𝑐^{3} \cosh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})}} & ← (147)式 \\ = & - \frac{𝑐^{2}}{𝑎} + \frac{𝑎 | \frac{𝑐^{5}}{𝑎^{2}} |}{𝑐^{3} \cosh [\frac{𝑎}{𝑐} {𝑡_{(5)} - \frac{𝑐 (4 𝑇₁ + 2 𝑇₂)}{𝑐}}]} & ←積分定数の値を代入した。 \\ = & - \frac{𝑐^{2}}{𝑎} + \frac{𝑐^{2}}{𝑎 \cosh \frac{𝑎 (𝑡_{(5)} - 4 𝑇₁ - 2 𝑇₂)}{𝑐}} & (154) \\ {𝑢_{(5)}}^{0} & = & \frac{𝑐^{6} \cosh^{2} {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})}}{𝑎^{2} 𝐾₁₀} & ← (148)式 \\ = & \frac{𝑐^{6} \cosh^{2} [\frac{𝑎}{𝑐} {𝑡_{(5)} - \frac{𝑐 (4 𝑇₁ + 2 𝑇₂)}{𝑐}}]}{𝑎^{2} \frac{𝑐^{5}}{𝑎^{2}}} & ←積分定数の値を代入した。 \\ = & 𝑐 \cosh^{2} \frac{𝑎 (𝑡_{(5)} - 4 𝑇₁ - 2 𝑇₂)}{𝑐} & (155) \\ {𝑢_{(5)}}^{1} & = & - \frac{𝐾₁₀}{| 𝐾₁₀ |} 𝑐 \sinh {\frac{𝑎}{𝑐} (𝑡_{(5)} - \frac{𝐾₁₂}{𝑐})} & ← (149)式 \\ = & - 1 𝑐 \sinh [\frac{𝑎}{𝑐} {𝑡_{(5)} - \frac{𝑐 (4 𝑇₁ + 2 𝑇₂)}{𝑐}}] & ←積分定数の値を代入した。 \\ = & - 𝑐 \sinh \frac{𝑎 (𝑡_{(5)} - 4 𝑇₁ - 2 𝑇₂)}{𝑐} & (156) \end{array}

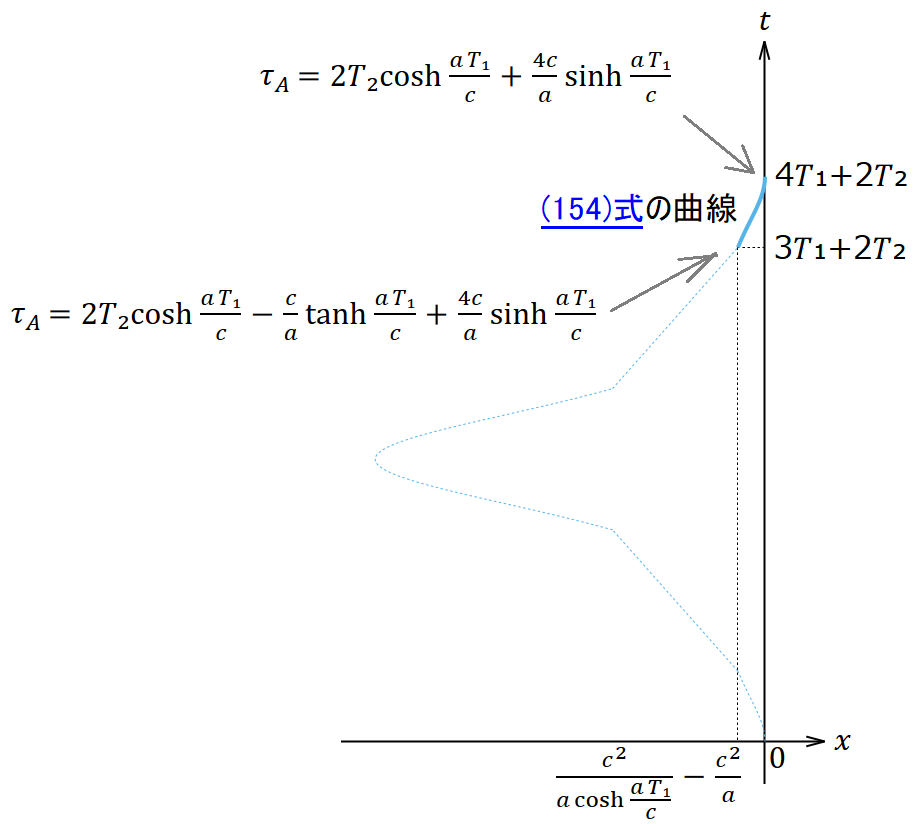
折り返し局面の終了時すなわち全行程の終了時では、 $𝑡_{(5)} = 4 𝑇₁ + 2 𝑇₂$ であるから、これを(154)式に代入すると $𝑥_{(5)} = 0$ となり、アリスがボブと同じ位置に帰還することを示す。また、(155)・(156)式に代入すると ${𝑢_{(5)}}^{0} = 𝑐$ , ${𝑢_{(5)}}^{1} = 0$ となり、この瞬間にアリスが静止する（ボブとの相対速度が0になる）ことを示す。一方、(153)式に代入するとアリスの固有時は $2 𝑇₂ \cosh \frac{𝑎 𝑇₁}{𝑐} + \frac{4 𝑐}{𝑎} \sinh \frac{𝑎 𝑇₁}{𝑐}$ となる。

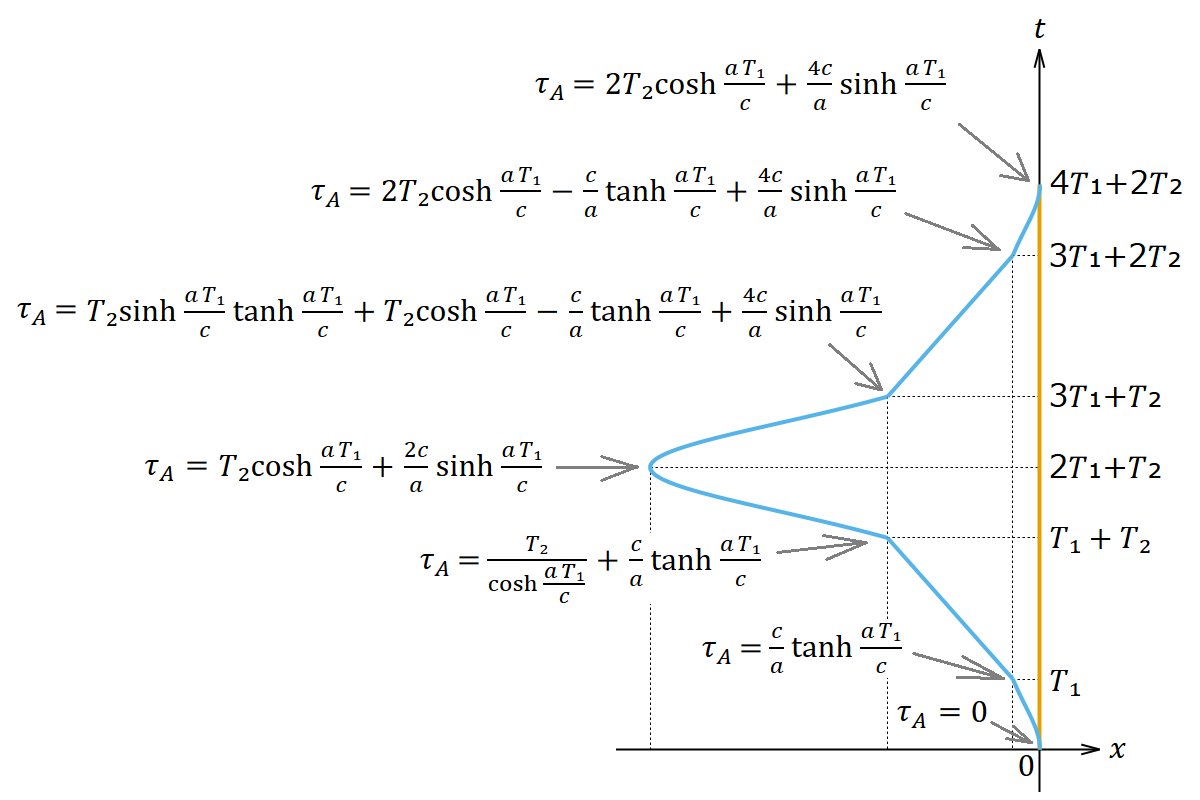
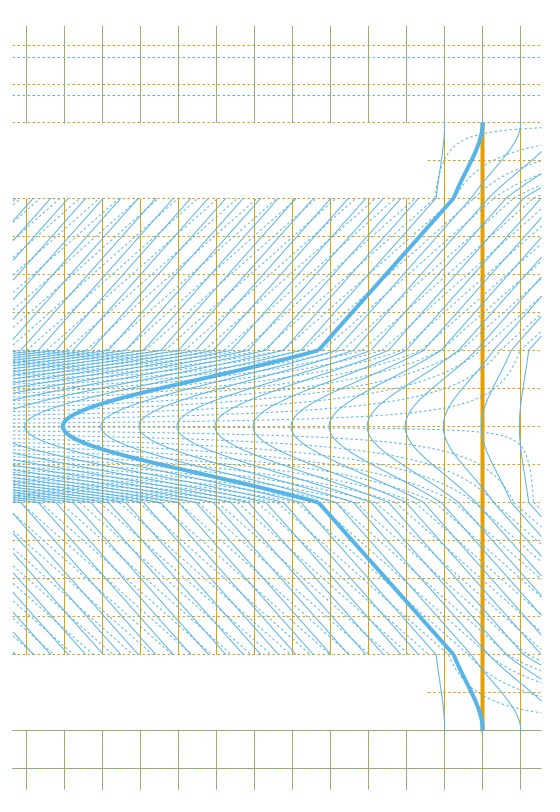
これで表1の右半分も算出できたことになる。

最後にまとめておくと、この章ではアリスの視点の慣性系のことは知らないふりをして、わざわざ一般相対性理論の手法を使ってボブの視点の座標系で重力場における運動方程式を解いてアリスの世界線および固有時を求めたのである。その結果、最終的なアリスの経過時間として、第A章でアリスの視点の慣性系で計算した結果と同じ結果が得られたわけである。以上により、アリス・ボブのどちらの視点の座標系で計算してもボブの時間が遅れるという一貫した同じ結果が導かれ、「双子のパラドックス」はパラドックスではないことを示す具体例が計算できた。