【3】 𝛬 ≠ 0, 256𝛬^²𝐾_𝑟^³ − 81𝛬𝐾_𝑚^⁴ − 432𝛬𝑘𝐾_𝑟𝐾_𝑚^² − 384𝛬𝑘^²𝐾_𝑟^² + 36𝑘^³𝐾_𝑚^² + 144𝑘^⁴𝐾_𝑟 = 0 のとき

今積分したい式は $$\int \frac{𝑎\mathrm{d𝑎}}{\sqrt{{𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4}}=\pm \int 𝑐\mathrm{d𝑡}({𝐾}_{𝑟}>0,{𝐾}_{𝑚}>0)\text{←}\text{(103)式}$$ である。 𝛬 ≠ 0 なら左辺の被積分関数は根号の中が4次式であるから一般にはこの積分は初等関数で表せない。だが $$256{𝛬}^2{{𝐾}_{𝑟}}^3-81𝛬{{𝐾}_{𝑚}}^4-432𝛬𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2-384𝛬{𝑘}^2{{𝐾}_{𝑟}}^2+36{𝑘}^3{{𝐾}_{𝑚}}^2+144{𝑘}^4{𝐾}_{𝑟}=0\text{(152)}$$ という条件が成り立っていれば初等的に積分することができる。この条件式は不等式ではなく等式である。これがたまたまぴったり成り立つことは現実にはたぶんないだろう。ただ、解を定性的な性質で分類するときに境界となるようなものがここに含まれているので、そういう観点では重要である。それにこれは前節における【4】に対応するものである。3.2節でやったのに3.3節でやらないのもバランスが悪いので、一応触れておくことにする。

まず(152)式がどこから出てきたかを説明しておこう。(103)式の左辺の被積分関数の根号の中は4次式であるが、それが運良く1次式の2乗を因数に持っていれば、それを根号の外に出すことができて根号の中は2次式となり積分ができる。ここではそのような場合を扱う。すなわち 𝐽, 𝑋, 𝑌, 𝑍 を未定の定数として、 $${𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4={(𝑎-𝐽)}^2(𝑋{𝑎}^2+𝑌𝑎+𝑍)\text{(153)}$$ のようになっていればよいのである。(153)式の右辺を展開すれば $${𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4=𝑋{𝑎}^4+(-2𝐽𝑋+𝑌){𝑎}^3+({𝐽}^2𝑋-2𝐽𝑌+𝑍){𝑎}^2+({𝐽}^2𝑌-2𝐽𝑍)𝑎+{𝐽}^2𝑍$$ であるから、 𝑎 の係数を比較すると $$\{\begin{array}{lllllll}\hfill 𝑋& & & & & \hfill =\hfill & \frac{𝛬}{3}\\ \hfill -2𝐽𝑋& \hfill +\hfill & \hfill 𝑌& & & \hfill =\hfill & 0\\ \hfill {𝐽}^2𝑋& \hfill -\hfill & \hfill 2𝐽𝑌& \hfill +\hfill & \hfill 𝑍& \hfill =\hfill & -𝑘\\ & & \hfill {𝐽}^2𝑌& \hfill -\hfill & \hfill 2𝐽𝑍& \hfill =\hfill & {𝐾}_{𝑚}\\ & & & & \hfill {𝐽}^2𝑍& \hfill =\hfill & {𝐾}_{𝑟}\end{array}\text{(154)}$$ となる。式が5つあるから制約も5つ出てくるわけだが、その内訳は、(153)式のような因数分解ができるために 𝛬, 𝑘, 𝐾_𝑟, 𝐾_𝑚 が満たすべき1つの関係と、それが満たされる場合の 𝐽, 𝑋, 𝑌, 𝑍 の4つの値である。

とりあえず 𝐽 は置いといて(154)式を 𝑋, 𝑌, 𝑍 の連立方程式だと思えば、第1式からそのまま $𝑋=\frac{𝛬}{3}$ であり、これを第2式に代入して変形すれば $𝑌=\frac{2𝛬𝐽}{3}$ となり、第5式より $𝑍=\frac{{𝐾}_{𝑟}}{{𝐽}^2}$ となる（第5式から 𝐽 ≠ 0 がわかる）。まだ使っていない残りの第3式・第4式にこれらの 𝑋, 𝑌, 𝑍 を代入すると $$\{\begin{array}{ll}-𝛬{𝐽}^2+\frac{{𝐾}_{𝑟}}{{𝐽}^2}=-𝑘& \text{(155)}\\ \frac{2𝛬{𝐽}^3}{3}-\frac{2{𝐾}_{𝑟}}{𝐽}={𝐾}_{𝑚}& \text{(156)}\end{array}$$ となる。(156)式の $\frac{3}{2𝐽}$ 倍を(155)式に足すと $$\begin{array}{lll}\hfill -\frac{2{𝐾}_{𝑟}}{{𝐽}^2}& =& -𝑘+\frac{3{𝐾}_{𝑚}}{2𝐽}\\ \hfill 0& =& -𝑘{𝐽}^2+\frac{3{𝐾}_{𝑚}}{2}𝐽+2{𝐾}_{𝑟}& \text{(157)}\end{array}$$ となる。今のところ 𝑘 の値は何も制限していないから0の可能性もある。もしも 𝑘 ≠ 0 ならば、(157)式より $$\begin{array}{lll}\hfill 𝐽& =& \frac{-\frac{3{𝐾}_{𝑚}}{2}\pm \sqrt{\frac{9{{𝐾}_{𝑚}}^2}{4}+8𝑘{𝐾}_{𝑟}}}{-2𝑘}\\ & =& \frac{3{𝐾}_{𝑚}\mp \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{4𝑘}& \text{(158)}\end{array}$$ である。あるいはこの分子と分母に $3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}$ （𝑘 ≠ 0 と仮定しているから、これは0でない。）を掛ければ $$\begin{array}{lll}\hfill 𝐽& =& \frac{9{{𝐾}_{𝑚}}^2-(9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟})}{4𝑘(3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}})}\\ & =& -\frac{8{𝐾}_{𝑟}}{3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}& \text{(159)}\end{array}$$ と書くこともできる。(158)式と(159)式は複号同順である。もしも 𝑘 = 0 ならば、(157)式より $$𝐽=-\frac{4{𝐾}_{𝑟}}{3{𝐾}_{𝑚}}\text{(160)}$$ である。ところで(158)式に 𝑘 = 0 を代入したら分母が0になってしまうので無意味だが、(159)式に 𝑘 = 0 を代入すると、複号の上を採用すれば(160)式と同じになり下を採用すれば発散する。したがって、発散する場合を除外することにしておけば 𝑘 が0であろうがなかろうが(159)式を使えばよいことになる。あとはこの 𝐽 を(155)式か(156)式に代入すれば(154)式の5連立方程式の最後の条件が判明する。単に代入しただけではわけのわからない形になるので、とりあえず 𝛬 について解いた形で表示してみよう。(159)式より $$\begin{array}{lll}\hfill \frac{1}{𝐽}& =& -\frac{3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{8{𝐾}_{𝑟}}\\ \hfill \frac{1}{{𝐽}^2}& =& \frac{9{{𝐾}_{𝑚}}^2+16𝑘{𝐾}_{𝑟}\pm 3{𝐾}_{𝑚}\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{32{{𝐾}_{𝑟}}^2}\\ \hfill \frac{1}{{𝐽}^3}& =& -\frac{9{𝐾}_{𝑚}(3{{𝐾}_{𝑚}}^2+8𝑘{𝐾}_{𝑟})\pm (9{{𝐾}_{𝑚}}^2+8𝑘{𝐾}_{𝑟})\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{128{{𝐾}_{𝑟}}^3}\\ \hfill \frac{1}{{𝐽}^4}& =& \frac{81{{𝐾}_{𝑚}}^4+288𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2+128{𝑘}^2{{𝐾}_{𝑟}}^2\pm 3{𝐾}_{𝑚}(9{{𝐾}_{𝑚}}^2+16𝑘{𝐾}_{𝑟})\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{512{{𝐾}_{𝑟}}^4}\end{array}$$ であるから、(155)式を使えば $$\begin{array}{llll}\hfill -𝛬{𝐽}^2+\frac{{𝐾}_{𝑟}}{{𝐽}^2}& =& -𝑘& \text{←}\text{(155)式}\\ \hfill 𝛬& =& \frac{𝑘}{{𝐽}^2}+\frac{{𝐾}_{𝑟}}{{𝐽}^4}\\ & =& 𝑘\cdot \frac{9{{𝐾}_{𝑚}}^2+16𝑘{𝐾}_{𝑟}\pm 3{𝐾}_{𝑚}\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{32{{𝐾}_{𝑟}}^2}\\ & & +{𝐾}_{𝑟}\cdot \frac{81{{𝐾}_{𝑚}}^4+288𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2+128{𝑘}^2{{𝐾}_{𝑟}}^2\pm 3{𝐾}_{𝑚}(9{{𝐾}_{𝑚}}^2+16𝑘{𝐾}_{𝑟})\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{512{{𝐾}_{𝑟}}^4}\\ & =& 3\cdot \frac{27{{𝐾}_{𝑚}}^4+144𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2+128{𝑘}^2{{𝐾}_{𝑟}}^2\pm {𝐾}_{𝑚}{(9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟})}^{\frac{3}{2}}}{512{{𝐾}_{𝑟}}^3}\end{array}$$ となり、(156)式を使えば $$\begin{array}{llll}\hfill \frac{2𝛬{𝐽}^3}{3}-\frac{2{𝐾}_{𝑟}}{𝐽}& =& {𝐾}_{𝑚}& \text{←}\text{(156)式}\\ \hfill 𝛬& =& \frac{3{𝐾}_{𝑚}}{2{𝐽}^3}+\frac{3{𝐾}_{𝑟}}{{𝐽}^4}\\ & =& \frac{3{𝐾}_{𝑚}}{2}\{-\frac{9{𝐾}_{𝑚}(3{{𝐾}_{𝑚}}^2+8𝑘{𝐾}_{𝑟})\pm (9{{𝐾}_{𝑚}}^2+8𝑘{𝐾}_{𝑟})\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{128{{𝐾}_{𝑟}}^3}\}\\ & & +3{𝐾}_{𝑟}\cdot \frac{81{{𝐾}_{𝑚}}^4+288𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2+128{𝑘}^2{{𝐾}_{𝑟}}^2\pm 3{𝐾}_{𝑚}(9{{𝐾}_{𝑚}}^2+16𝑘{𝐾}_{𝑟})\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{512{{𝐾}_{𝑟}}^4}\\ & =& 3\cdot \frac{27{{𝐾}_{𝑚}}^4+144𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2+128{𝑘}^2{{𝐾}_{𝑟}}^2\pm {𝐾}_{𝑚}{(9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟})}^{\frac{3}{2}}}{512{{𝐾}_{𝑟}}^3}\end{array}$$ となって、当然ながら同じ結果が出てくる。分数の横線が長すぎて書きくいからばらして $$𝛬=3\{\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}\pm {𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\}\text{(161)}$$ と書いておこう。(158)・(159)式と(161)式は複号同順であり、この先もこのページでは 𝛬 と 𝐽 は最下行までずっと複号同順である（(103)式の右辺についている複号に対してはまったく関係なく複号任意である）。3桁の数値係数とかあってめんどくさそうだが、分母の数値係数はすべて2のべき乗、分子の数値係数はすべて3のべき乗で統一されている。それがどうしたと言われても困るが。

結局、幸運にも 𝛬 の値が(161)式のようになっているならば、(153)式より $$\begin{array}{ll}{𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4={(𝑎-𝐽)}^2(\frac{𝛬}{3}{𝑎}^2+\frac{2𝛬𝐽}{3}𝑎+\frac{{𝐾}_{𝑟}}{{𝐽}^2})& \text{(162)}\\ \text{ただし}𝐽=-\frac{8{𝐾}_{𝑟}}{3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}& \text{←}\text{(159)式}\end{array}$$ のように書けるということだ。ただし本来(161)式は 𝛬, 𝑘, 𝐾_𝑟, 𝐾_𝑚 の4つの定数の間の関係を表すものだが、この書き方だと 𝛬 だけ独立性が失われて他の3定数に依存しているかのような印象を与える恐れがあり公平性を欠いているし、複号や無理式があってややこしい。そこで少し変形すると $$\begin{array}{llll}\hfill 𝛬& =& 3\{\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}\pm {𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\}& \text{←}\text{(161)式}\\ \hfill 𝛬-3(\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}})& =& \pm 3{𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\\ \hfill {\{𝛬-3(\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}\left)\right\}}^2& =& 9{{𝐾}_{𝑚}}^2{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^3\\ \hfill {𝛬}^2-3𝛬(\frac{27{{𝐾}_{𝑚}}^4}{256{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{16{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{2{𝐾}_{𝑟}})+9(\frac{729{{𝐾}_{𝑚}}^8}{262144{{𝐾}_{𝑟}}^6}+\frac{243𝑘{{𝐾}_{𝑚}}^6}{8192{{𝐾}_{𝑟}}^5}+\frac{27{𝑘}^2{{𝐾}_{𝑚}}^4}{256{{𝐾}_{𝑟}}^4}+\frac{9{𝑘}^3{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^3}+\frac{{𝑘}^4}{16{{𝐾}_{𝑟}}^2})& =& 9{{𝐾}_{𝑚}}^2(\frac{729{{𝐾}_{𝑚}}^6}{262144{{𝐾}_{𝑟}}^6}+\frac{243𝑘{{𝐾}_{𝑚}}^4}{8192{{𝐾}_{𝑟}}^5}+\frac{27{𝑘}^2{{𝐾}_{𝑚}}^2}{256{{𝐾}_{𝑟}}^4}+\frac{{𝑘}^3}{8{{𝐾}_{𝑟}}^3})\\ \hfill {𝛬}^2-\frac{81𝛬{{𝐾}_{𝑚}}^4}{256{{𝐾}_{𝑟}}^3}-\frac{27𝛬𝑘{{𝐾}_{𝑚}}^2}{16{{𝐾}_{𝑟}}^2}-\frac{3𝛬{𝑘}^2}{2{𝐾}_{𝑟}}+\frac{9{𝑘}^3{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^3}+\frac{9{𝑘}^4}{16{{𝐾}_{𝑟}}^2}& =& 0\\ \hfill 256{𝛬}^2{{𝐾}_{𝑟}}^3-81𝛬{{𝐾}_{𝑚}}^4-432𝛬𝑘{𝐾}_{𝑟}{{𝐾}_{𝑚}}^2-384𝛬{𝑘}^2{{𝐾}_{𝑟}}^2+36{𝑘}^3{{𝐾}_{𝑚}}^2+144{𝑘}^4{𝐾}_{𝑟}& =& 0& \text{←}\text{(152)式}\end{array}$$ のようになり、(152)式が導かれた。見た目はこちらのほうが簡潔である……というほど簡潔でもないが整数係数の斉次多項式になった。(152)式がどこから出てきたかの説明はこれで終わりだ。

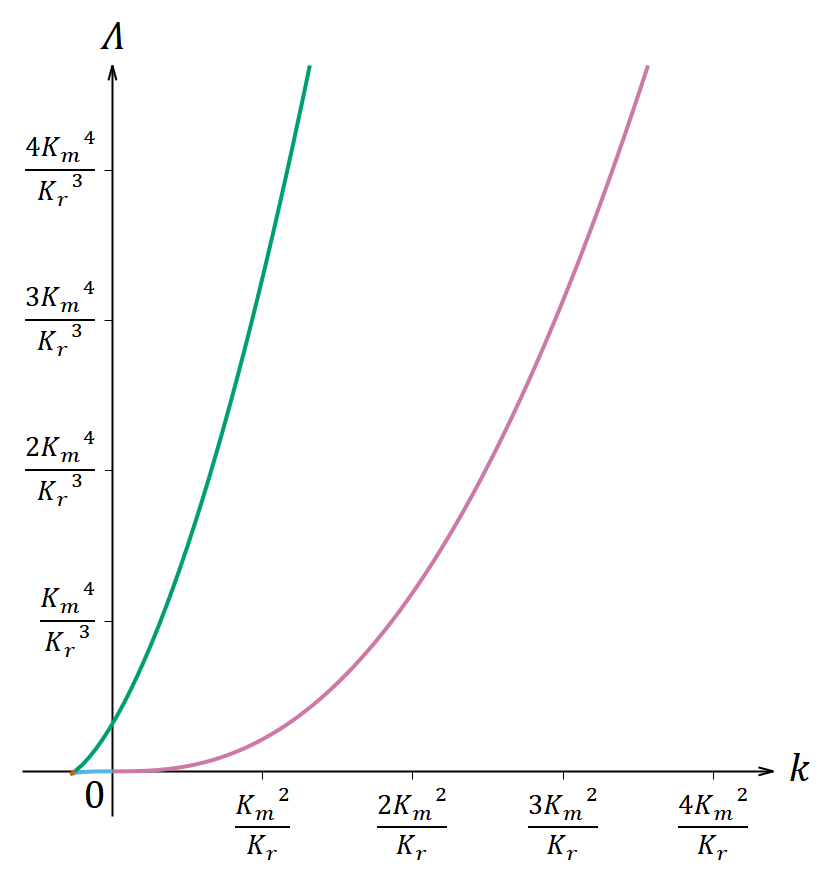
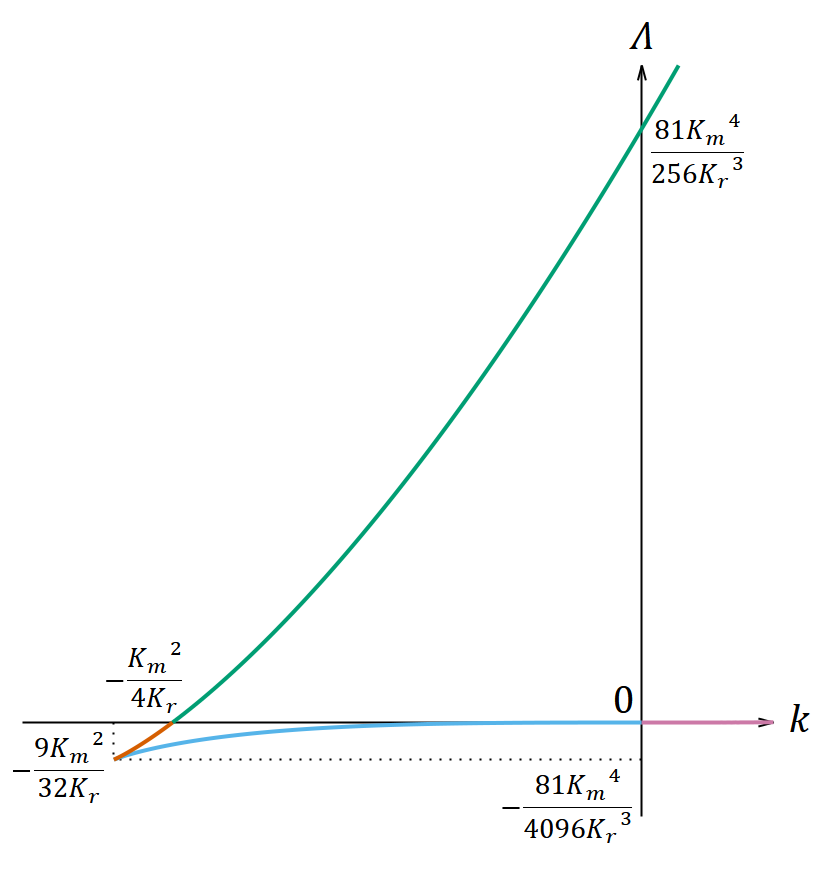
(152)式または(161)式が満たされるのがどういう場合なのかを視覚的に表示したものが図3である。別にこんな図を描かなくても正しく式変形を行えば原理的にはこの先の計算をすることはできるが、この図を把握していた方が理解しやすいだろうと思う。

ところで(158)・(159)式の 𝐽 も、右辺に 𝛬 だけ入っていなくて不公平だし複号や根号があってややこしいではないか、と思うのであれば、 $$𝐽=-\frac{4{𝐾}_{𝑟}(9𝛬{{𝐾}_{𝑚}}^2+8𝛬𝑘{𝐾}_{𝑟}-6{𝑘}^3)}{3{𝐾}_{𝑚}(9𝛬{{𝐾}_{𝑚}}^2+16𝛬𝑘{𝐾}_{𝑟}-4{𝑘}^3)}\text{(163)}$$ とか $$𝐽=-\frac{3{𝐾}_{𝑚}(4𝛬{𝐾}_{𝑟}+{𝑘}^2)}{9𝛬{{𝐾}_{𝑚}}^2+8𝛬𝑘{𝐾}_{𝑟}-6{𝑘}^3}\text{(164)}$$ のように書くこともできる。(152)式が成り立っている限り(163)式と(164)式の値は等しい。ただし $𝑘=-\frac{9{{𝐾}_{𝑚}}^2}{32{𝐾}_{𝑟}}$ , $𝛬=-\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3}$ のときは(152)式が成り立つけれども(163)・(164)式は右辺が分子も分母も0になってしまうので使えない。(163)・(164)式が使えるのは $𝑘>-\frac{9{{𝐾}_{𝑚}}^2}{32{𝐾}_{𝑟}}$ , $𝛬>-\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3}$ のときである。なお $𝑘<-\frac{9{{𝐾}_{𝑚}}^2}{32{𝐾}_{𝑟}}$ または $𝛬<-\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3}$ のときはどうやっても(152)式が成り立たない。(163)・(164)式の導出は読者への演習問題とする。

ついでに、この後で何度か使う表式があるので今それを計算しておく。(156)式より $$\begin{array}{llll}\hfill \frac{2𝛬{𝐽}^3}{3}-\frac{2{𝐾}_{𝑟}}{𝐽}& =& {𝐾}_{𝑚}& \text{←}\text{(156)式}\\ \hfill \frac{2𝛬{𝐽}^3}{3}& =& {𝐾}_{𝑚}+\frac{2{𝐾}_{𝑟}}{𝐽}\\ \hfill \frac{𝛬{𝐽}^3}{{𝐾}_{𝑚}}& =& 3(\frac{1}{2}+\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}𝐽})\\ & =& 3\{\frac{1}{2}+\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}(-\frac{3{𝐾}_{𝑚}\pm \sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{8{𝐾}_{𝑟}}\left)\right\}\\ & =& \frac{3}{8}(1\mp 3\sqrt{1+\frac{32𝑘{𝐾}_{𝑟}}{9{{𝐾}_{𝑚}}^2}})& \text{(165)}\end{array}$$ である。これももちろん(158)・(159)・(161)式と複号同順である。

では本題の積分を始めよう。(152)式または(161)式が成り立っているとき、(162)式より $$\begin{array}{llll}\hfill {𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4& =& {(𝑎-𝐽)}^2(\frac{𝛬}{3}{𝑎}^2+\frac{2𝛬𝐽}{3}𝑎+\frac{{𝐾}_{𝑟}}{{𝐽}^2})& \text{←}\text{(162)式}\\ & =& {(𝑎-𝐽)}^2\{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{𝛬{𝐽}^2}{3}+\frac{{𝐾}_{𝑟}}{{𝐽}^2}\}\\ & =& {(𝑎-𝐽)}^2\{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{1}{2𝐽}(\frac{2𝛬{𝐽}^3}{3}-\frac{2{𝐾}_{𝑟}}{𝐽}\left)\right\}\\ & =& {(𝑎-𝐽)}^2\{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{{𝐾}_{𝑚}}{2𝐽}\}& \text{←}\text{(156)式}\text{を代入した。}\text{(166)}\end{array}$$ のようになるから、これを使って(103)式を変形すると $$\begin{array}{llll}\hfill \int \frac{𝑎\mathrm{d𝑎}}{\sqrt{{𝐾}_{𝑟}+{𝐾}_{𝑚}𝑎-𝑘{𝑎}^2+\frac{𝛬}{3}{𝑎}^4}}& =& \pm \int 𝑐\mathrm{d𝑡}& \text{←}\text{(103)式}\\ \hfill \int \frac{𝑎\mathrm{d𝑎}}{\sqrt{{(𝑎-𝐽)}^2\{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{{𝐾}_{𝑚}}{2𝐽}\}}}& =& \pm \int 𝑐\mathrm{d𝑡}& \text{←}\text{(166)式}\text{を代入した。}\\ \hfill \int \frac{𝑎\mathrm{d𝑎}}{|𝑎-𝐽|\sqrt{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{{𝐾}_{𝑚}}{2𝐽}}}& =& \pm \int 𝑐\mathrm{d𝑡}\end{array}$$ となって根号の中が簡単になる。右辺の全体に複号がついているから左辺の符号がひっくり返っても等式の意味は変わらないので、左辺の被積分関数の分母の絶対値記号はあってもなくても同じだからはずすと、 $$\begin{array}{lll}\hfill \int \frac{𝑎\mathrm{d𝑎}}{(𝑎-𝐽)\sqrt{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{{𝐾}_{𝑚}}{2𝐽}}}& =& \pm \int 𝑐\mathrm{d𝑡}\\ \hfill \int (1+\frac{𝐽}{𝑎-𝐽})\frac{\mathrm{d𝑎}}{\sqrt{\frac{𝛬}{3}{(𝑎+𝐽)}^2-\frac{{𝐾}_{𝑚}}{2𝐽}}}& =& \pm \int 𝑐\mathrm{d𝑡}& \text{(167)}\end{array}$$ となる。ここからさらに 𝛬 と 𝐽 の符号によって場合分けをする。