第4章 解の定性的な分類
第2章・第3章でいろいろな条件の下でフリードマン方程式の解を求めてきた。多くの異なる解が現れたが、それらの細かい違いは無視して大まかな定性的な特徴を考えてみよう。ここで言う定性的な特徴とは、具体的には 𝑎 がとりうる範囲と および の符号のことである。
第3章で考えたフリードマン方程式は であった。3種類の式があるが、(100)式で仮に 𝐾𝑚 = 0 とすれば(13)式と同じになるし、 𝐾𝑟 = 0 とすれば(42)式と同じになる。だから(100)式で 𝐾𝑚 か 𝐾𝑟 が0でもよいことにしておけば(100)式だけを考えれば済むので、ここからはそのようにしよう。ただし 𝐾𝑚 と 𝐾𝑟 の両方が同時に0である場合は考えないこととする(それは別の記事「真空の宇宙に対するフリードマン方程式を解く」と同じ状況であるからそっちを見てほしい)。
ここでは(100)式が初等的に積分できる場合も含めて、改めて解の特徴を記述する。やることは3.3節の【5】の焼き直しであるから、説明は簡単に済ませることにする。(100)式より、 である。ここで と置くと(223)式は となる。(224)式の左辺は2乗だから0以上なので、右辺も0以上でなければならない。したがって 𝑎 は 𝑓(𝑎) ≧ 𝑘 を満たす範囲のみを動くことができる。
𝛬 の符号に応じて、 𝑎 と 𝑓(𝑎) の関係は図6のようになる。
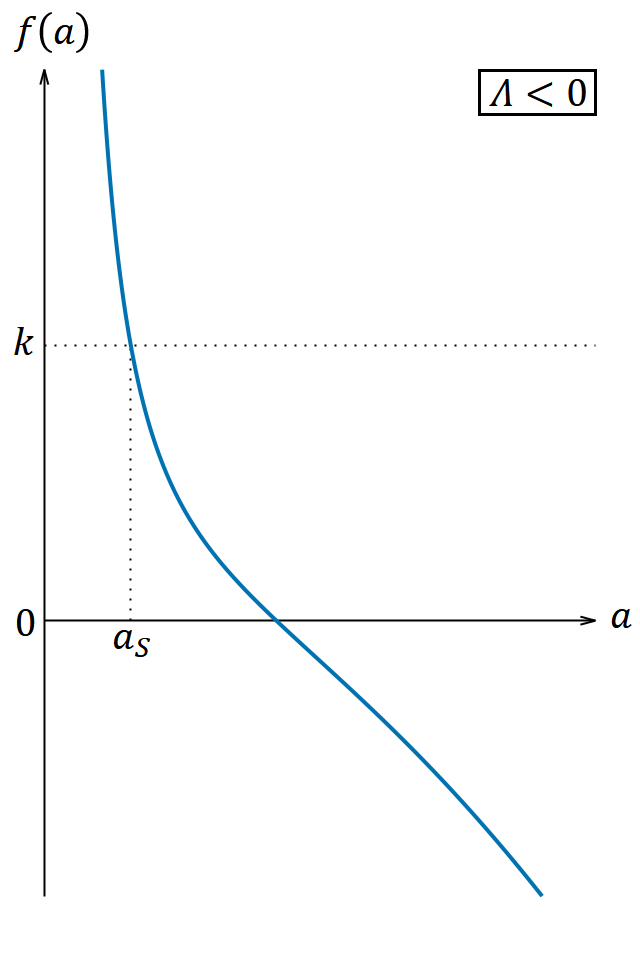
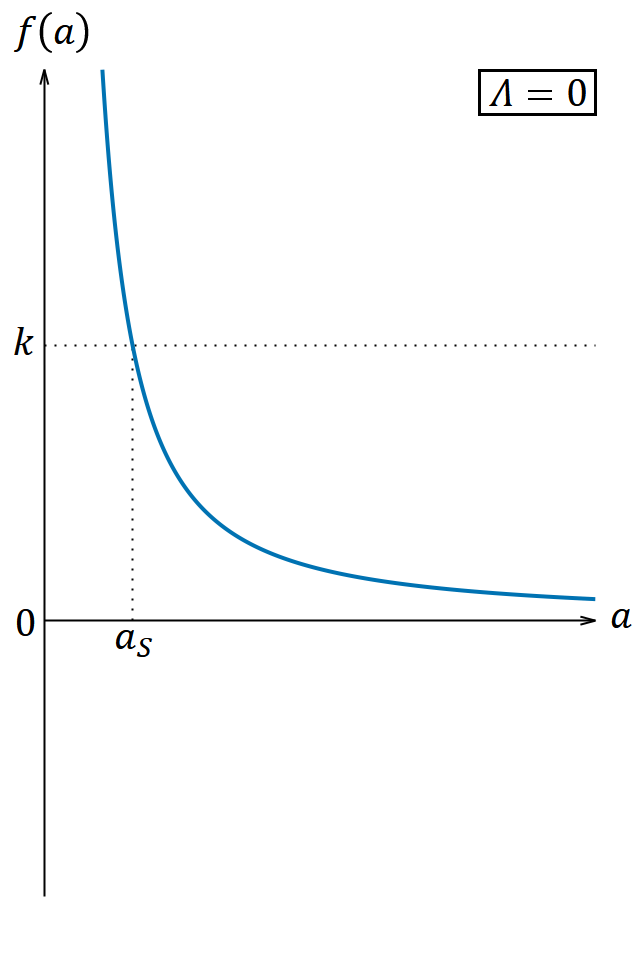
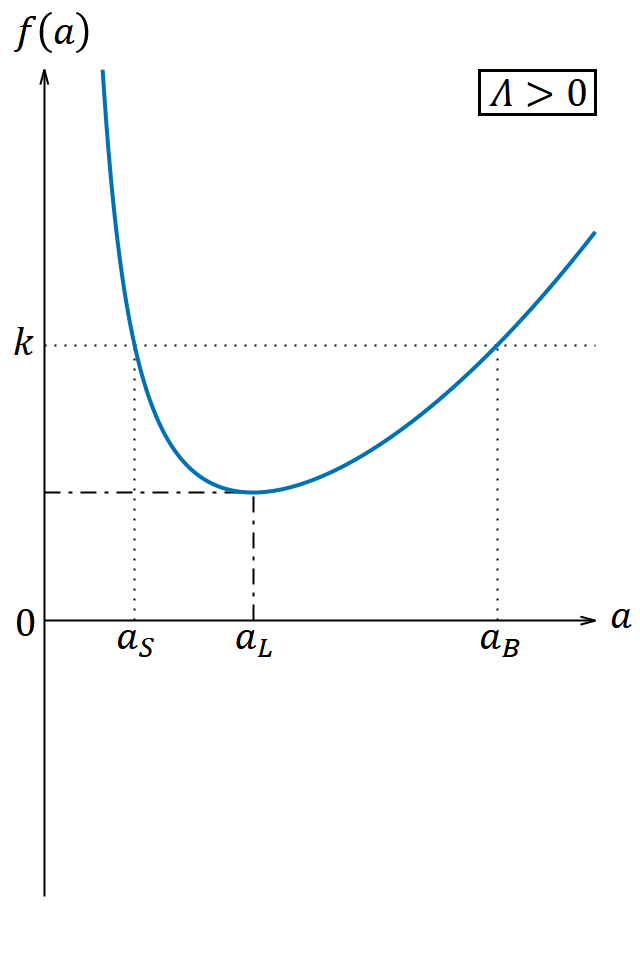
図6は 𝐾𝑚 と 𝐾𝑟 のうちどちらか一方が0でも定性的な性質は変わらない。これに基づき、解は 𝛬 と 𝑘 の値に従って次のように分類される。
① 𝛬 < 0 のときと、 𝛬 = 0 , 𝑘 > 0 のとき
𝑓(𝑎𝑆) = 𝑘, 𝑎𝑆 > 0 とすれば解が取り得る範囲は 0 ≦ 𝑎 ≦ 𝑎𝑆 である。これは有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値 𝑎 = 𝑎𝑆 になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。
② 𝛬 = 0 , 𝑘 ≦ 0 のとき
𝑎 は0以上のすべての値をとることができる。解は互いに時間反転となる2つの解(膨張解と収縮解)が存在する。膨張解は有限の時刻に 𝑎 = 0 から始まって減速膨張し、無限の未来に 𝑎 → ∞ になる宇宙である。収縮解はその時間反転である。ここでさらに 𝑘 = 0 のときと 𝑘 < 0 のときに分ける考え方もあるが、ここでは面倒なのでそこまで細分化しない。
③ 𝛬 > 0 , 𝑘 > 𝑓(𝑎𝐿) のとき
𝑓(𝑎𝑆) = 𝑓(𝑎𝐵) = 𝑘, 0 < 𝑎𝑆 < 𝑎𝐵 とすれば解が取り得る範囲は 0 ≦ 𝑎 ≦ 𝑎𝑆 および 𝑎𝐵 ≦ 𝑎 であり、以下のようになる。
- 0 ≦ 𝑎 ≦ 𝑎𝑆 となる解
- ①と同じで、有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値 𝑎 = 𝑎𝑆 になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。
- 𝑎𝐵 ≦ 𝑎 となる解
- 無限の過去に 𝑎 → ∞ だったものが減速収縮し、最小値 𝑎 = 𝑎𝐵 になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。
④ 𝛬 > 0 , 𝑘 = 𝑓(𝑎𝐿) のとき
𝑎 は0以上のすべての値をとることができるのだが、個別の解に関しては 𝑎 の範囲に制限が生じ、以下のようになる。
- 0 ≦ 𝑎 < 𝑎𝐿 となる解
- 互いに時間反転となる2つの解(膨張解と収縮解)が存在する。膨張解は有限の時刻に 𝑎 = 0 から始まって減速膨張し、無限の未来に 𝑎 = 𝑎𝐿 になる宇宙である。収縮解はその時間反転である。
- 𝑎 = 𝑎𝐿 となる解
- 無限の過去から無限の未来まで 𝑎 = 𝑎𝐿 である定常な宇宙である。
- 𝑎𝐿 < 𝑎 となる解
- 互いに時間反転となる2つの解(膨張解と収縮解)が存在する。膨張解は無限の過去に 𝑎 = 𝑎𝐿 だったものが加速膨張し、無限の未来に 𝑎 → ∞ になる宇宙である。収縮解はその時間反転である。
⑤ 𝛬 > 0 , 𝑘 < 𝑓(𝑎𝐿) のとき
𝑎 は0以上のすべての値をとることができる。解は互いに時間反転となる2つの解(膨張解と収縮解)が存在する。膨張解は有限の時刻に 𝑎 = 0 から始まって減速膨張し、 𝑎 = 𝑎𝐿 になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。収縮解はその時間反転である。
𝛬 > 0 のときに③〜⑤の境界となる 𝑘 = 𝑓(𝑎𝐿) という条件の具体的な表式は、「𝑘 = …」という形で書くのは面倒だから「𝛬 = …」という形で書けば である。分母に無理式があるのが気に入らないかもしれないが、分母を有理化すると 𝐾𝑟 = 0 のときに分子も分母も0になってしまい別扱いを要するから、それを避けるために意図的にこうしているのである。 𝛬 > 0, 𝑘 > 0 のとき、 𝛬 が(225)式より小さければ③、大きければ⑤である。 𝛬 > 0 , 𝑘 ≦ 0 のときはいつでも⑤である。(225)式は 𝐾𝑚 = 0 ならば(31)式の 𝑘 > 0 の範囲と同じであり、 𝐾𝑟 = 0 ならば(74)式の 𝑘 > 0 の範囲と同じであり、 𝐾𝑟 も 𝐾𝑚 も正ならば(161)式で複号を−にした式の 𝑘 > 0 の範囲(図3のピンク色の曲線)と同じである。
①〜⑤のすべての解の概略図を図7に示す。
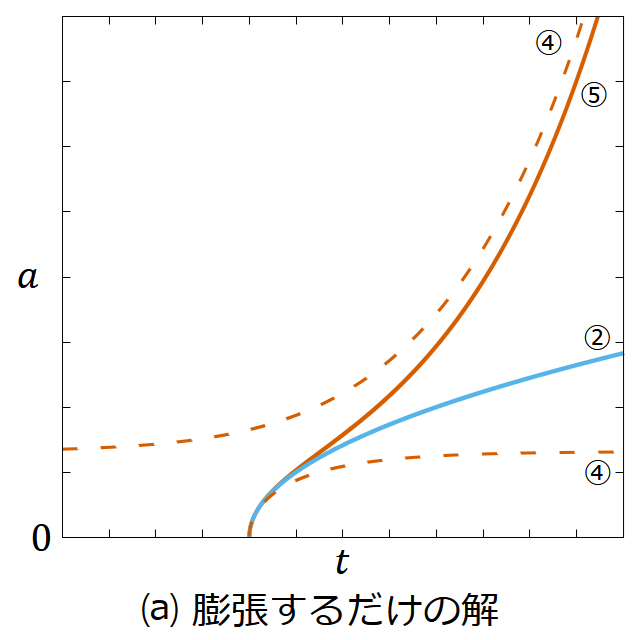
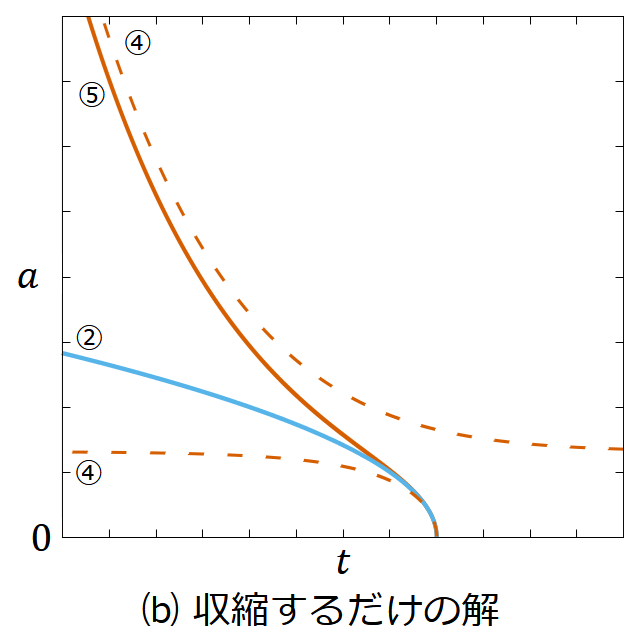
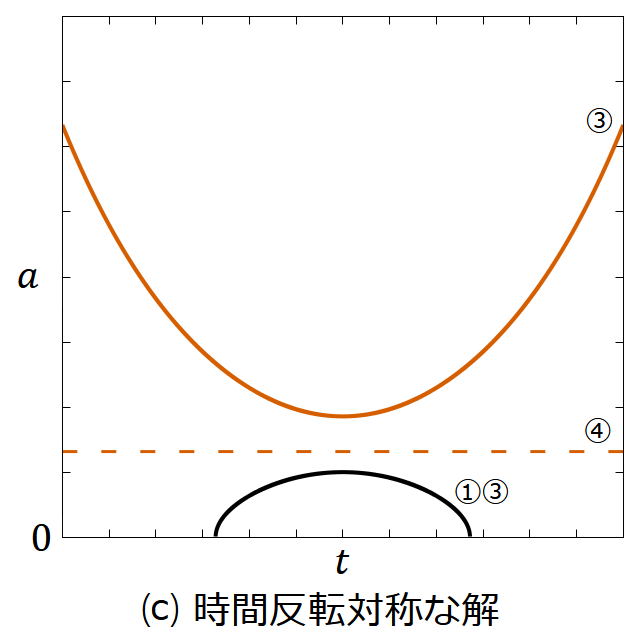
図7. フリードマン方程式の解の定性的な分類。すべての解を1つの図に書き込むと線が入り乱れて見にくくなるので、⒜ 膨張するだけの解、⒝ 収縮するだけの解、⒞ 時間反転対称な解の3つの図に分けて表示してある。⒜と⒝は互いに時間反転の関係にある。
黒色の線は 𝛬 の符号に関わらず可能な解、水色の線は 𝛬 = 0 のときのみ可能な解、茶色の線は 𝛬 > 0 のときのみ可能な解である。破線は④の解である。
𝛬 が負ならば1種類の解しかない。 𝛬 が正ならば多様な解の可能性が生まれる。④以外の解は過去や未来を見ると、有限の時刻に 𝑎 = 0 となって解の端に達するか無限の過去・未来に 𝑎 → ∞ に発散するかのどちらかである。無限に過去や未来に行っても 𝑎 が0にならず発散もしない場合があるのは④だけである。だが④の解は、 𝑘 = 𝑓(𝑎𝐿) すなわち(225)式がぴったり成り立っていなければならないから、実現するのは難しそうだ。第2章・第3章の各節で求めた解がこの分類どおりになっていることは読者自ら確認されたい。
今回は状態方程式として、普通の物質と光(放射)のものを用いた。その場合に出てくるフリードマン方程式の解はこれですべてである。比較的おとなしい解ばかりだ。 𝑎 が正の値を保ったまま膨張と収縮を交互に繰り返すような解とか、有限の時刻に 𝑎 → ∞ に発散してしまうような激しい解は出てこなかった。もっと奇妙な性質をもつ別の状態方程式を採用すれば異なる解が出てくる可能性はある。
これらの解の中で、現実のこの宇宙に当てはまる解がどれなのか(あるいはどれも当てはまらないのか)は、観測した結果と比較して決められることになる。