光や物質で満たされた宇宙に対するフリードマン方程式を解く(4)

【4】 9𝛬𝐾_𝑚^² = 4𝑘^³ ≠ 0 のとき

𝛬 ≠ 0 かつ 𝑘 ≠ 0 の場合で初等的に積分する方法を私が知っているのはこの条件が成り立つときだけである。(74)式より 𝛬 と 𝑘 は同符号である。ここでと置くと、この 𝐽 も 𝛬 や 𝑘 と同符号であり、次のような量を計算すると、 $式を代入した。式を代入した。$ のようになるから、これを使って(45)式を変形すると $式式を代入した。$ となって根号の中が簡単になる。右辺の全体に複号がついているから左辺の符号がひっくり返っても等式の意味は変わらないので、左辺の被積分関数の分母の絶対値記号はあってもなくても同じだからはずすと、となる。ここからさらに 𝛬 と 𝑘 の符号によって場合分けをする。

【4‐1】 9𝛬𝐾_𝑚^² = 4𝑘^³ < 0 のとき

このとき 𝛬 と 𝑘 は負であり、 𝐽 も負である。(77)式は $式$ となる。ここで置換積分するに当たって、新しい変数を 𝑢 として真っ先に思いつく方法は根号の中を 𝑢^² と置くことかもしれないが、ここでは都合によりと置く。ただし 𝑢 は正ものを選ぶこととする。別にでなく 𝑢^² と置いたって積分はできるのだが、このようにした理由は後で説明する。これだと 𝑎 = 0 となる点が表現できないではないかと心配になるかもしれないが、どうせ当節の大本のフリードマン方程式(42)式は 𝑎 = 0 のときに発散するのでそこを気にしても無駄である。 𝑢 → +∞ の極限をとれば 𝑎 → +0 の極限が計算できるのでそれでよしとしておこう。すると、であるから、これらを(78)式に代入すると $式・・式を代入した。$ となる。ここで積分の公式 $（は積分定数）$ を使って(82)式を積分すると $（積分定数をとした。）$ となる。 𝑢 を元に戻せばである。とりあえずこれで解の表式は求まった。さて、この形のままでも構わないのだが、 arctan の中に根号があったり、 𝑎 → +0 のときに arctan の引数が+∞に発散する（が、そのとき arctan 自体の値は有限でに収束する）というのはあまり格好良くないし、解の挙動を把握するのが面倒である。もうちょっと見やすい形に変形してみよう。

三角関数の最も基本的な関係式の一つであるを使うとが得られるので、これを使うと cos の2倍角の公式からが得られる。(84)式の 𝜓 に具体的な表式を代入すると、以下ではいずれもであることに注意して変形すれば、 $のとき$ $のとき$ となる。これらを(83)式に代入すれば、解は $ただし$ のように書くことができ、だいぶマシな形になった。しかし逆に 𝑎 を 𝑡 の初等関数で書くことはできないだろう。

𝑢 = 0 すなわち 𝑎 = −2𝐽 のときは(78)式の左辺の被積分関数の分母が0になってしまうので除外して考えてきたが、(44)式までさかのぼってみるとそのときも 0 = 0 となってちゃんと成り立っている。よって 𝑎 = −2𝐽 のときも(85)式は解である。これは時刻に 𝑎 = 0 から始まって減速膨張し、時刻 𝑡 = 0 に最大値 𝑎 = −2𝐽 になって加速収縮に転じ、時刻に 𝑎 = 0 になって終わる宇宙である。複号の−が膨張期で複号の+が収縮期である。

ところで(79)式の変数変換で置換積分をしたときに左辺を 𝑢^² でなくと置いた理由の説明が後回しになっていた。その理由は、 𝑢^² と置いて置換積分すると解の膨張期と収縮期とで積分定数の値を変えなければならなくなる（そうしないと 𝑎 が最大値をとる時刻がずれて、同じ時刻で両者がつながらない）ので、説明や解の表記がめんどくさくなるからだ。ただそれだけの理由である。 cos 関数の逆関数は多価関数だが、 arccos 関数はその中から1個の分枝（値域が [0, 𝜋] となるもの）だけを勝手に選んでいるから、そういうことが起きるのだ。具体的にどうなるのか想像ができなければ、実際にやってみるがよい。

【4‐2】 9𝛬𝐾_𝑚^² = 4𝑘^³ > 0 のとき

このとき 𝛬 と 𝑘 は正であり、 𝐽 も正である。(77)式は $式$ となる。ここで置換積分するに当たって、新しい変数を 𝑢 としてと置く。ただし 𝑢 は非負のものを選ぶこととする。先ほど【4‐1】では本質的でない手間を回避するために 𝑢^² でなくと置いたが、今回はそのような手間は生じないので素直に 𝑢^² にしておく。すると、であるから、これらを(86)式に代入すると $式・・式を代入した。$ となる。これを積分するのは簡単である。左辺の被積分関数をのように変形できることはすぐにわかるから、あとはこの各項を項別に積分すればよい。それで正解が得られるし何も間違っていない。ただその結果を元の変数 𝑎 で表すと、対数 ln の引数に根号を含む分数式が現れたりして、ごちゃごちゃしたわけのわからない形になる。そこで、見やすくするために【4‐1】と似たような流れで積分を行ってみたい。ここで積分の公式 $（は積分定数）$ を使って(90)式を積分すると、 $のとき積分定数をとした。$ $のとき積分定数をとした。$ となる。 𝑢 は1以上にはならない。 𝑢 を元に戻せばである。とりあえずこれで解の表式は求まった。さて、この形のままでも構わないのだが、 artanh の中に根号があるのはあまり格好良くないし、解の挙動を把握するのが面倒である。もうちょっと見やすい形に変形してみよう。

双曲線関数の最も基本的な関係式の一つであるを使うとが得られるので、これを使うと cosh の2倍角の公式からが得られる。(93)式の 𝜓 に具体的な表式を代入すると、以下ではいずれも 𝜓 ≧ 0 であることに注意して変形すれば、 $のとき$ $のとき$ $のとき$ となる。これらを(92)式に代入すれば、解は $したがってただし$ のように書くことができ、だいぶマシな形になった。しかし逆に 𝑎 を 𝑡 の初等関数で書くことはできないだろう。

この解には物理的には4つの解が含まれている。複号が+の解の 0 ≦ 𝑎 < 𝐽 の範囲は、時刻 𝑡 = 0 に 𝑎 = 0 から始まって減速膨張し、無限の未来に 𝑎 = 𝐽 になる宇宙である。複号が−の解の 0 ≦ 𝑎 < 𝐽 の範囲はその時間反転である。複号が+の解の 𝐽 < 𝑎 の範囲は、無限の過去に 𝑎 → ∞ だったものが減速収縮し、無限の未来に 𝑎 = 𝐽 になる宇宙である。複号が−の解の 𝐽 < 𝑎 の範囲はその時間反転である。

それにしても、 9𝛬𝐾_𝑚^² = 4𝑘^³ などという(74)式の関係式が偶然にもぴったり成り立つなんてことはまず起こらないだろう、数学的にはあり得るかもしれないが物理的には特に考えなくてもよさそうである。……と思うかもしれないが、ルメートル先生の1927年の論文 “Un Univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extra‐galactiques” では、この関係式の下で解を求めている。それも「この場合なら解析的に積分できるから」みたいなしょうもない理由ではなく、（現代の知識とは合わないが当時としては）きちんとした物理的な根拠に基づいて、この宇宙ではこの関係式が（少なくとも近似的には）成り立たねばならないと論じている。その論文の須藤靖先生による日本語訳は須藤靖編「20世紀科学論文集現代宇宙論の誕生」（岩波書店）に収録されているので興味があれば読んでみるとよい。ハッブル先生の論文より先にハッブル・ルメートルの法則（旧称「ハッブルの法則」）を示しハッブル定数の値を求めていたことで21世紀に入ってから話題になった論文である。

ところで(94)式では 𝑎 は 𝐽 以外のすべての非負の値を取り得るが、有限の時刻に 𝑎 = 𝐽 になることがない。では今の関係式の下で初期条件を 𝑎 = 𝐽 としたらフリードマン方程式の解がないのかといえば、そんなことはなくて、その場合は恒等的に 𝑎 = 𝐽 となる定数関数が解になる。それは第2章で出てきた「アインシュタインの静止宇宙」に他ならない。ではなぜ今の計算でその解が出てこなかったのかわかるだろうか。この章では最初から定数関数を除外しているから、というのはそのとおりだが、式変形のどの段階で除外されたのかという話である。わかる人は良いが、わからない人のために説明しておこう。この節の最初の方で(44)式の下で「両辺は恒等的に0でないから」という断り書きを付けて右辺の表式で両辺を割っているところがある。 𝑎 が定数関数だった場合は、そこは「両辺は恒等的に0」になるから、0で割ることになってしまってそれ以降の式変形が意味を持たなくなるのだ。その時点で定数関数である可能性が捨てられている。

【5】それ以外のとき

「それ以外」とは、 𝛬 も 𝑘 も0でなく、 9𝛬𝐾_𝑚^² ≠ 4𝑘^³ のときである。このときは初等的に積分することはできない（できる場合もあるかもしれないが私は知らない）ので、近似的な話にとどめておく。

今の場合のフリードマン方程式より、 $式$ である。ここでと置くと(43)式はとなる。(95)式の左辺は2乗だから0以上なので、右辺も0以上でなければならない。したがって 𝑎 は 𝑓(𝑎) ≧ 𝑘 を満たす範囲のみを動くことができる。 𝑎 と 𝑓(𝑎) の関係を調べるために 𝑓(𝑎) の1〜2階微分を計算すると次のようになる。ここからさらに 𝛬 の符号によって場合分けをする。

【5‐1】それ以外で 𝛬 < 0 のとき

𝑎 と 𝑓(𝑎) の関係は図1のようになる。 𝑓(𝑎) は 𝑎 > 0 において単調減少であり、上限や下限はなくすべての実数をとる。

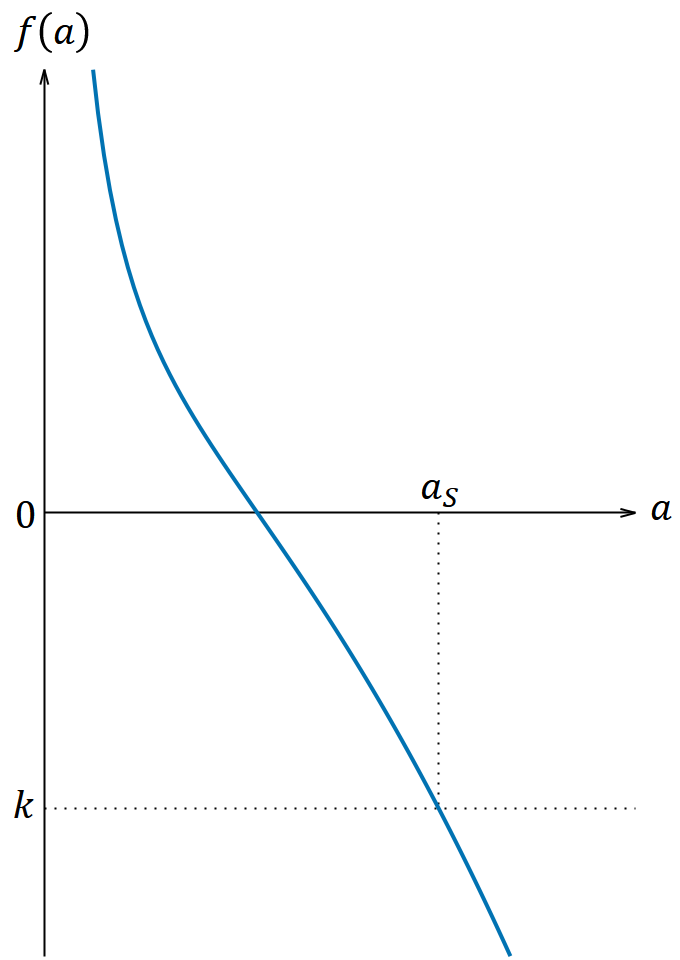
𝑘 の値が何であっても、 𝑎 が取りうる値に制限が生じる。例えば 𝑘 が図1に描いたところにあれば、 𝑎 は図1の 𝑎_𝑆 より大きい値をとることができない。つまり 𝑓(𝑎_𝑆) = 𝑘, 𝑎_𝑆 > 0 とすれば解が取り得る範囲は 0 ≦ 𝑎 ≦ 𝑎_𝑆 である。

𝑎 ≈ 0 の辺りでは(43)式の右辺は第1項が他を圧倒するから、第1項以外を無視すればのようになる。これは【1】のアインシュタイン・ドジッター宇宙と同じような状況だから、そのときの解である(46)式を流用して近似的にとすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 0 になるように取ってある。これは 𝑎 = 0 から始まる減速膨張宇宙または 𝑎 = 0 で終わる加速収縮宇宙である。

𝑎 ≈ 𝑎_𝑆 の辺りでは 𝑓(𝑎) を1次までのテーラー展開で近似するとであるからこれを(95)式に代入するととなり、両辺は恒等的に0でないから $（積分定数をとした。）$ となる。この式が表す曲線は (𝑡, 𝑎) = (0, 𝑎_𝑆) を頂点（最大値）とする放物線である。これは極大値 𝑎 = 𝑎_𝑆 になる時刻を境に減速膨張から加速収縮に転じる宇宙である。（欲張って 𝑓(𝑎) を2次までのテーラー展開で近似して同じように計算すれば、放物線だったところが懸垂線 (𝑘 > 0) またはサインカーブ (𝑘 < 0) になるけれども、しょせん近似なので面倒なだけであまり得るものはないであろう。）

𝑎 ≈ 0 と 𝑎 ≈ 𝑎_𝑆 の間では、が0を超えて符号を変える機会がないからずっと膨張またはずっと収縮であり、 𝑎 ≈ 0 における近似解と 𝑎 ≈ 𝑎_𝑆 における近似解を滑らかにつないだようなものになるはずだ（その際に時間座標 𝑡 の原点を適切に設定しなおす必要がある）。したがってこの解は、有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値 𝑎 = 𝑎_𝑆 になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。

𝑎 の最大値 𝑎_𝑆 は 𝑓(𝑎) = 𝑘 の正の解だから $のときのときのとき$ である。ここで【4‐1】や【3‐1】の場合も含めてのときは 𝑎 の最大値をという共通の表式で書くこともできる。いや、のときもそのように書いて間違いとは言えないが、そのときは∛の中身が虚数になるから3つある3乗根のどれを指しているかわからなくなるから避けたほうが無難だろう。

フリードマン先生の1922年の論文 “Über die Krümmung des Raumes” （を樽家篤史先生が日本語に訳したもの。須藤靖編「20世紀科学論文集現代宇宙論の誕生」（岩波書店）に収録。）では、この解で表される正曲率 (𝑘 > 0) の宇宙を「periodische Welt （周期世界）」と呼んでいる。ただし、数学的には無限に繰り返される周期解になるようだが、物理的にはスケール因子が0になる瞬間は特異点となりその先に解を延ばせないので、この解は有限の寿命を持った宇宙である。

【5‐2】それ以外で 𝛬 > 0 のとき

𝑎 と 𝑓(𝑎) の関係は図2のようになる。 𝑓(𝑎) はスケール因子がある値 𝑎 = 𝑎_𝐿 のときに最小値 𝑓(𝑎_𝐿) をとる。 𝑓(𝑎) は 0 < 𝑎 < 𝑎_𝐿 において減少し 𝑎_𝐿 < 𝑎 において増加し、どちらの区間でも上限はなく 𝑓(𝑎_𝐿) より大きいすべての実数をとる。 𝑎_𝐿 に関する具体的な表式は , , 𝑓′(𝑎_𝐿) = 0 , 𝑓″(𝑎_𝐿) = 2𝛬 である。

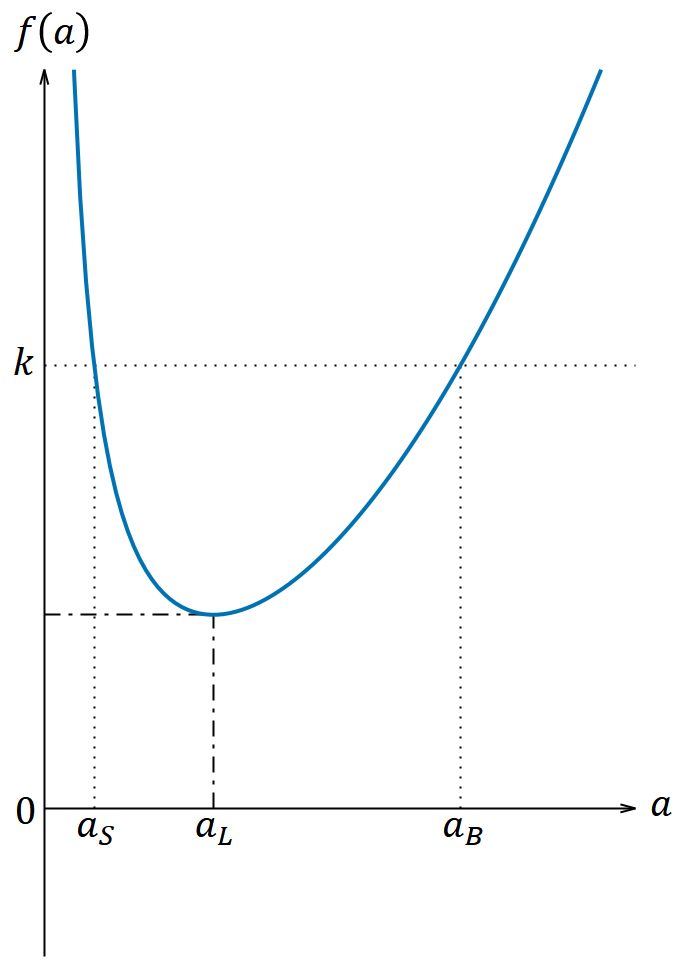
今度は 𝑘 の値に応じて解の定性的な挙動が変わり、3通りの解が考えられる。 𝑘 > 𝑓(𝑎_𝐿) ならば、 𝑎 が取りうる値に制限が生じる。例えば 𝑘 が図2に描いたところにあれば、 𝑎 は図2の 𝑎_𝑆 と 𝑎_𝐵 の間の値をとることができない。つまり 𝑓(𝑎_𝑆) = 𝑓(𝑎_𝐵) = 𝑘, 0 < 𝑎_𝑆 < 𝑎_𝐵 とすれば解がとりうる範囲は 0 ≦ 𝑎 ≦ 𝑎_𝑆 および 𝑎_𝐵 ≦ 𝑎 である。 𝑘 < 𝑓(𝑎_𝐿) ならば、 𝑎 は0以上のすべての値をとることができる。なお 𝑘 = 𝑓(𝑎_𝐿) となるのは【4‐2】の場合であるからすでに解は求まっており、今の話の対象外である。

① 𝑘 > 𝑓(𝑎_𝐿) の場合で 0 ≦ 𝑎 ≦ 𝑎_𝑆 となる解

近似の考え方は【5‐1】と同じである。これは有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。フリードマン論文（樽家訳）ではこの解で表される宇宙も「periodische Welt （周期世界）」に分類している。

② 𝑘 > 𝑓(𝑎_𝐿) の場合で 𝑎_𝐵 ≦ 𝑎 となる解

𝑎 ≈ 𝑎_𝐵 の辺りでは 𝑓(𝑎) を1次までのテーラー展開で近似するとであるからこれを(95)式に代入するととなり、両辺は恒等的に0でないから $（積分定数をとした。）$ となる。この式が表す曲線は (𝑡, 𝑎) = (0, 𝑎_𝐵) を頂点（最小値）とする放物線である。これは極小値 𝑎 = 𝑎_𝐵 になる時刻を境に減速収縮から加速膨張に転じる宇宙である。（欲張って 𝑓(𝑎) を2次までのテーラー展開で近似して同じように計算すれば、放物線だったところが懸垂線になるけれども、しょせん近似なので面倒なだけであまり得るものはないであろう。）

𝑎 → ∞ の辺りでは(43)式の右辺は第3項が他を圧倒するから、第3項以外を無視すればのようになる。これは別の記事「真空の宇宙に対するフリードマン方程式を解く」のドジッター宇宙と同じような状況だから、そのときの解を流用して近似的にとすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 1 になるように取ってある。これは無限の未来に 𝑎 → ∞ になる加速膨張宇宙または無限の過去に 𝑎 → ∞ だった減速収縮宇宙である。

𝑎 ≈ 𝑎_𝐵 と 𝑎 → ∞ の間では、が0を超えて符号を変える機会がないからずっと膨張またはずっと収縮であり、 𝑎 ≈ 𝑎_𝐵 における近似解と 𝑎 → ∞ における近似解を滑らかにつないだようなものになるはずだ（その際に時間座標 𝑡 の原点を適切に設定しなおす必要がある）。したがってこの解は、無限の過去に 𝑎 → ∞ だったものが減速収縮し、最小値になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。

フリードマン論文（樽家訳）では、この解で表される宇宙のうち最小値 𝑎 = 𝑎_𝐵 となる時刻以降を「monotone Welt zweiter Art （第2種の単調な世界）」と呼んでいる。

③ 𝑘 < 𝑓(𝑎_𝐿) の場合の解 (0 ≦ 𝑎)

𝑎 ≈ 0 の辺りでは近似の考え方は①や【5‐1】と同じであり、 $式$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 0 になるように取ってある。これは 𝑎 = 0 から始まる減速膨張宇宙または 𝑎 = 0 で終わる加速収縮宇宙である。

𝑎 ≈ 𝑎_𝐿 の辺りでは 𝑓(𝑎) を2次までのテーラー展開で近似するとであるからこれを(95)式に代入するととなり、両辺は恒等的に0でないから $（積分定数をとした。）$ となる。これは 𝑎 = 𝑎_𝐿 になる時刻を境に減速膨張から加速膨張に転じる宇宙または 𝑎 = 𝑎_𝐿 になる時刻を境に減速収縮から加速収縮に転じる宇宙である。

𝑎 → ∞ の辺りでは近似の考え方は②と同じであり、 $式$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 1 になるように取ってある。これは無限の未来に 𝑎 → ∞ になる加速膨張宇宙または無限の過去に 𝑎 → ∞ だった減速収縮宇宙である。

𝑎 ≈ 0 と 𝑎 ≈ 𝑎_𝐿 と 𝑎 → ∞ の間では、が0を超えて符号を変える機会がないからずっと膨張またはずっと収縮であり、 𝑎 ≈ 0 における近似解と 𝑎 ≈ 𝑎_𝐿 における近似解と 𝑎 → ∞ における近似解を滑らかにつないだようなものになるはずだ（その際に時間座標 𝑡 の原点を適切に設定しなおす必要がある）。したがってこの解のうち膨張解は、有限の時刻に 𝑎 = 0 から始まって減速膨張し、になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。収縮解はその時間反転である。フリードマン論文（樽家訳）では、この解で表される正曲率 (𝑘 > 0) の膨張宇宙を「monotone Welt erster Art （第1種の単調な世界）」と呼んでいる。

光や物質で満たされた宇宙に対するフリードマン方程式を解く(4)

【4】 9𝛬𝐾𝑚² = 4𝑘³ ≠ 0 のとき

【4‐1】 9𝛬𝐾𝑚² = 4𝑘³ < 0 のとき

【4‐2】 9𝛬𝐾𝑚² = 4𝑘³ > 0 のとき

【5】 それ以外のとき

【5‐1】 それ以外で 𝛬 < 0 のとき

【5‐2】 それ以外で 𝛬 > 0 のとき

① 𝑘 > 𝑓(𝑎𝐿) の場合で 0 ≦ 𝑎 ≦ 𝑎𝑆 となる解

② 𝑘 > 𝑓(𝑎𝐿) の場合で 𝑎𝐵 ≦ 𝑎 となる解

③ 𝑘 < 𝑓(𝑎𝐿) の場合の解 (0 ≦ 𝑎)

解のまとめ

MathJax（数式表示用 JavaScript）使用設定

説明