【5】 それ以外のとき

「それ以外」とは、 𝛬 が0でなく、【3】や【4】でやった条件に当てはまらないときである。このときは初等的に積分することはできない（できる場合もあるかもしれないが私は知らない）ので、近似的な話にとどめておく。

今の場合のフリードマン方程式より、 $${\dot{𝑎}}^2=\frac{{𝐾}_{𝑟}}{{𝑎}^2}+\frac{{𝐾}_{𝑚}}{𝑎}-𝑘+\frac{𝛬}{3}{𝑎}^2\text{←}\text{(101)式}$$ である。ここで $$𝑓\left(𝑎\right)=\frac{{𝐾}_{𝑟}}{{𝑎}^2}+\frac{{𝐾}_{𝑚}}{𝑎}+\frac{𝛬}{3}{𝑎}^2$$ と置くと(101)式は $${\dot{𝑎}}^2=𝑓\left(𝑎\right)-𝑘\text{(220)}$$ となる。(220)式の左辺は2乗だから0以上なので、右辺も0以上でなければならない。したがって 𝑎 は 𝑓(𝑎) ≧ 𝑘 を満たす範囲のみを動くことができる。 𝑎 と 𝑓(𝑎) の関係を調べるために 𝑓(𝑎) の1〜2階微分を計算すると次のようになる。 $$\begin{array}{l}{𝑓}^{\prime }\left(𝑎\right)=\frac{\mathrm{d}𝑓\left(𝑎\right)}{\mathrm{d𝑎}}=-\frac{2{𝐾}_{𝑟}}{{𝑎}^3}-\frac{{𝐾}_{𝑚}}{{𝑎}^2}+\frac{2𝛬}{3}𝑎\\ {𝑓}^{″}\left(𝑎\right)=\frac{{\mathrm{d}}^2𝑓\left(𝑎\right)}{{\mathrm{d𝑎}}^2}=\frac{6{𝐾}_{𝑟}}{{𝑎}^4}+\frac{2{𝐾}_{𝑚}}{{𝑎}^3}+\frac{2𝛬}{3}\end{array}$$ ここからさらに 𝛬 の符号によって場合分けをする。

【5‐1】 それ以外で 𝛬 < 0 のとき

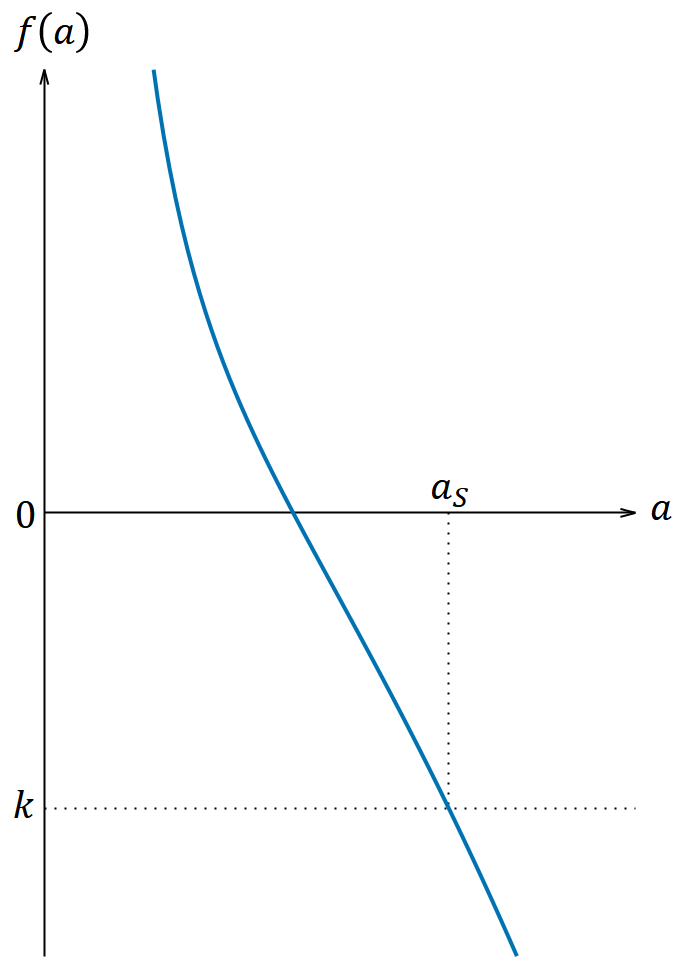
𝑎 と 𝑓(𝑎) の関係は図4のようになる。 𝑓(𝑎) は 𝑎 > 0 において単調減少であり、上限や下限はなくすべての実数をとる。

𝑘 の値が何であっても、 𝑎 が取りうる値に制限が生じる。例えば 𝑘 が図4に描いたところにあれば、 𝑎 は図4の 𝑎_𝑆 より大きい値をとることができない。つまり 𝑓(𝑎_𝑆) = 𝑘, 𝑎_𝑆 > 0 とすれば解が取り得る範囲は 0 ≦ 𝑎 ≦ 𝑎_𝑆 である。

𝑎 ≈ 0 の辺りでは(101)式の右辺は第1項が他を圧倒するから、第1項以外を無視すれば $${\dot{𝑎}}^2\approx \frac{{𝐾}_{𝑟}}{{𝑎}^2}$$ のようになる。これは3.1節の「光で満たされた宇宙」の【1】と同じような状況だから、そのときの解である(16)式を流用して近似的に $$𝑎\approx \sqrt[4]{{𝐾}_{𝑟}}\sqrt{\pm 2𝑐𝑡}\text{(221)}$$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 0 になるように取ってある。これは 𝑎 = 0 から始まる減速膨張宇宙または 𝑎 = 0 で終わる加速収縮宇宙である。

𝑎 ≈ 𝑎_𝑆 の辺りでは近似の考え方は3.2節の「ダスト流体で満たされた宇宙」の【5‐1】と同じであるからそのときの(97)式を流用して $$𝑎\approx {𝑎}_{𝑆}+\frac{1}{4}{𝑓}^{\prime }\left({𝑎}_{𝑆}\right){\left(𝑐𝑡\right)}^2\text{←}\text{(97)式}$$ とすることができる。この式が表す曲線は (𝑡, 𝑎) = (0, 𝑎_𝑆) を頂点（最大値）とする放物線である。これは極大値 𝑎 = 𝑎_𝑆 になる時刻を境に減速膨張から加速収縮に転じる宇宙である。

𝑎 ≈ 0 と 𝑎 ≈ 𝑎_𝑆 の間では、 $\dot{𝑎}$ が0を超えて符号を変える機会がないからずっと膨張またはずっと収縮であり、 𝑎 ≈ 0 における近似解と 𝑎 ≈ 𝑎_𝑆 における近似解を滑らかにつないだようなものになるはずだ（その際に時間座標 𝑡 の原点を適切に設定しなおす必要がある）。したがってこの解は、有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値 𝑎 = 𝑎_𝑆 になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。

𝑎 の最大値 𝑎_𝑆 は 𝑓(𝑎) = 𝑘 の正の解だから $$\begin{array}{l}{𝑎}_{𝑆}=\frac{𝐽}{2}(1+\sqrt{-1+\frac{6𝑘}{𝛬{𝐽}^2}-\frac{6{𝐾}_{𝑚}}{𝛬{𝐽}^3}})\\ \text{ただし}\\ 𝐽=\sqrt{\frac{1}{𝛬}(\sqrt[3]{𝑀+\sqrt{{𝑀}^2-{𝑁}^3}}+\sqrt[3]{𝑀-\sqrt{{𝑀}^2-{𝑁}^3}}+2𝑘)}\\ 𝑀=\frac{9}{2}𝛬{{𝐾}_{𝑚}}^2+12𝛬𝑘{𝐾}_{𝑟}-{𝑘}^3\\ 𝑁=4𝛬{𝐾}_{𝑟}+{𝑘}^2\end{array}$$ である。ここで 𝑀^² < 𝑁^³ のときは 𝐽 を定義する式の中に2つある∛の中身がともに虚数になる。その場合はそれぞれ3つずつある虚数3乗根のどれを採用しても構わないが、2つの∛が互いに複素共役になる組み合わせを選ぶこととする。そうすればちゃんと 𝐽 が実数になり、 𝑎_𝑆 は同一の値になるはずだ。 𝑀^² ≧ 𝑁^³ のときは∛の中身が実数になり、そのときは∛は唯一の実数3乗根を指すものとする。なお 𝑀^² = 𝑁^³ のときは(152)式が成り立つからすでに【3‐1】で積分できており今の話の対象外であるが、今の話をそのまま適用することもできる。

【5‐2】 それ以外で 𝛬 > 0 のとき

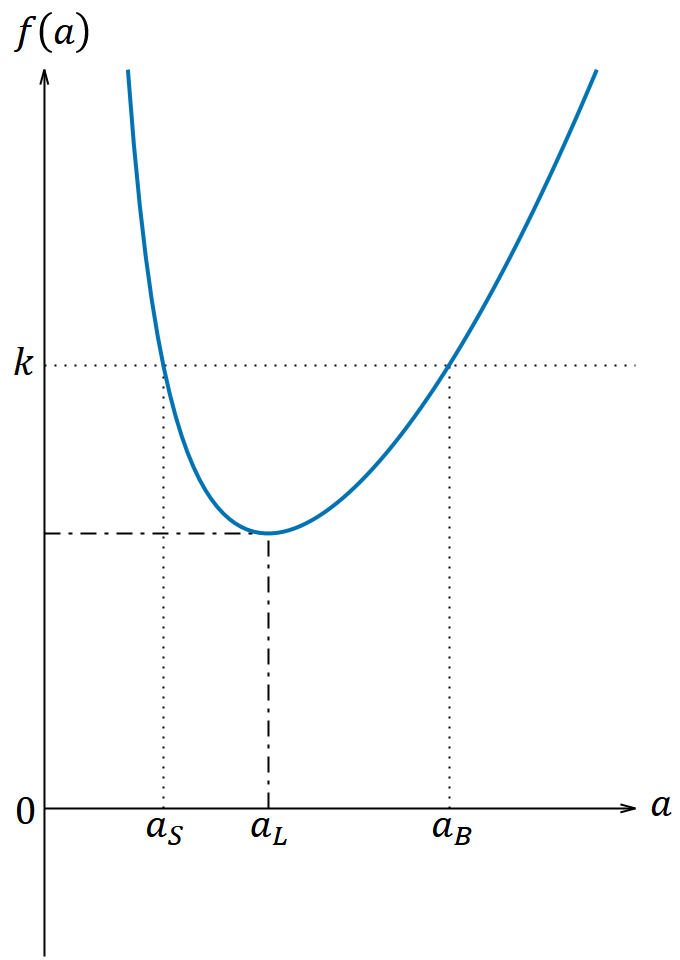
𝑎 と 𝑓(𝑎) の関係は図5のようになる。 𝑓(𝑎) はスケール因子がある値 𝑎 = 𝑎_𝐿 のときに最小値 𝑓(𝑎_𝐿) をとる。 𝑓(𝑎) は 0 < 𝑎 < 𝑎_𝐿 において減少し 𝑎_𝐿 < 𝑎 において増加し、どちらの区間でも上限はなく 𝑓(𝑎_𝐿) より大きいすべての実数をとる。 𝑎_𝐿 は具体的には $$\begin{array}{l}{𝑎}_{𝐿}=\frac{𝐽}{2}(1+\sqrt{\frac{3{𝐾}_{𝑚}}{𝛬{𝐽}^3}-1})\\ \text{ただし}\\ 𝐽=\sqrt[4]{𝑁}\sqrt{2\sinh \left(\frac{1}{3}\mathrm{arsinh}\frac{𝑀}{{𝑁}^{\frac{3}{2}}}\right)}=\sqrt{\sqrt[3]{𝑀+\sqrt{{𝑀}^2+{𝑁}^3}}+\sqrt[3]{𝑀-\sqrt{{𝑀}^2+{𝑁}^3}}}\\ 𝑀=\frac{9{{𝐾}_{𝑚}}^2}{8{𝛬}^2}\\ 𝑁=\frac{4{𝐾}_{𝑟}}{𝛬}\end{array}$$ であり、 𝑓(𝑎_𝐿) > 0 , 𝑓′(𝑎_𝐿) = 0 , 𝑓″(𝑎_𝐿) > 0 である。

今度は 𝑘 の値に応じて解の定性的な挙動が変わり、3通りの解が考えられる。 𝑘 > 𝑓(𝑎_𝐿) ならば、 𝑎 が取りうる値に制限が生じる。例えば 𝑘 が図5に描いたところにあれば、 𝑎 は図5の 𝑎_𝑆 と 𝑎_𝐵 の間の値をとることができない。つまり 𝑓(𝑎_𝑆) = 𝑓(𝑎_𝐵) = 𝑘, 0 < 𝑎_𝑆 < 𝑎_𝐵 とすれば解がとりうる範囲は 0 ≦ 𝑎 ≦ 𝑎_𝑆 および 𝑎_𝐵 ≦ 𝑎 である。 𝑘 < 𝑓(𝑎_𝐿) ならば、 𝑎 は0以上のすべての値をとることができる。なお 𝑘 = 𝑓(𝑎_𝐿) となるのは【3‐2】の場合であるからすでに解は求まっており、今の話の対象外である。

① 𝑘 > 𝑓(𝑎_𝐿) の場合で 0 ≦ 𝑎 ≦ 𝑎_𝑆 となる解

近似の考え方は【5‐1】と同じである。これは有限の時刻に 𝑎 = 0 から始まって減速膨張し、最大値 𝑎 = 𝑎_𝑆 になったときに加速収縮に転じ、有限の時刻に 𝑎 = 0 になって終わる宇宙である。 𝑎 の最大値 𝑎_𝑆 は 𝑓(𝑎) = 𝑘 の2つある正の解のうち小さい方だから $$\begin{array}{ll}{𝑎}_{𝑆}=\frac{𝐽}{2}(1-\sqrt{-1+\frac{6𝑘}{𝛬{𝐽}^2}-\frac{6{𝐾}_{𝑚}}{𝛬{𝐽}^3}})& \text{(222)}\\ \text{ただし}\\ 𝐽=\sqrt{\frac{2}{𝛬}\left\{\sqrt{𝑁}\cos \right(\frac{1}{3}\arccos \frac{𝑀}{{𝑁}^{\frac{3}{2}}})+𝑘\}}\\ 𝑀=\frac{9}{2}𝛬{{𝐾}_{𝑚}}^2+12𝛬𝑘{𝐾}_{𝑟}-{𝑘}^3\\ 𝑁=4𝛬{𝐾}_{𝑟}+{𝑘}^2\end{array}$$ である。

② 𝑘 > 𝑓(𝑎_𝐿) の場合で 𝑎_𝐵 ≦ 𝑎 となる解

近似の考え方は3.2節の「ダスト流体で満たされた宇宙」の【5‐2】②と同じである。これは無限の過去に 𝑎 → ∞ だったものが減速収縮し、最小値 𝑎 = 𝑎_𝐵 になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。 𝑎 の最小値 𝑎_𝐵 は 𝑓(𝑎) = 𝑘 の2つある正の解のうち大きい方だから、上の①の(222)式と同じ 𝑀 , 𝑁 , 𝐽 を使って $$\begin{array}{l}{𝑎}_{𝐵}=\frac{𝐽}{2}(1+\sqrt{-1+\frac{6𝑘}{𝛬{𝐽}^2}-\frac{6{𝐾}_{𝑚}}{𝛬{𝐽}^3}})\\ \text{ただし}𝐽\text{は}\text{(222)式}\text{と同じ}\end{array}$$ である。

③ 𝑘 < 𝑓(𝑎_𝐿) の場合の解 (0 ≦ 𝑎)

𝑎 ≈ 0 の辺りでは近似の考え方は①や【5‐1】と同じであるから、そのときの(221)式を流用して $$𝑎\approx \sqrt[4]{{𝐾}_{𝑟}}\sqrt{\pm 2𝑐𝑡}\text{←}\text{(221)式}$$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 0 になるように取ってある。これは 𝑎 = 0 から始まる減速膨張宇宙または 𝑎 = 0 で終わる加速収縮宇宙である。

𝑎 ≈ 𝑎_𝐿 の辺りでは近似の考え方は3.2節の「ダスト流体で満たされた宇宙」の【5‐2】③と同じであるからそのときの(99)式を流用して $$𝑎\approx {𝑎}_{𝐿}+\sqrt{\frac{2\{𝑓\left({𝑎}_{𝐿}\right)-𝑘\}}{{𝑓}^{″}\left({𝑎}_{𝐿}\right)}}\sinh \{\pm \sqrt{\frac{{𝑓}^{″}\left({𝑎}_{𝐿}\right)}{2}}𝑐𝑡\}\text{←}\text{(99)式}$$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 𝑎_𝐿 になるように取ってある。これは 𝑎 = 𝑎_𝐿 になる時刻を境に減速膨張から加速膨張に転じる宇宙または 𝑎 = 𝑎_𝐿 になる時刻を境に減速収縮から加速収縮に転じる宇宙である。

𝑎 → ∞ の辺りでは近似の考え方は②と同じであるから、同様に3.2節の「ダスト流体で満たされた宇宙」の【5‐2】②の(98)式を流用して $$𝑎\approx \exp (\pm \sqrt{\frac{𝛬}{3}}𝑐𝑡)\text{←}\text{(98)式}$$ とすることができる。ただし時間座標 𝑡 は 𝑡 = 0 のときに 𝑎 = 1 になるように取ってある。これは無限の未来に 𝑎 → ∞ になる加速膨張宇宙または無限の過去に 𝑎 → ∞ だった減速収縮宇宙である。

𝑎 ≈ 0 と 𝑎 ≈ 𝑎_𝐿 と 𝑎 → ∞ の間では、 $\dot{𝑎}$ が0を超えて符号を変える機会がないからずっと膨張またはずっと収縮であり、 𝑎 ≈ 0 における近似解と 𝑎 ≈ 𝑎_𝐿 における近似解と 𝑎 → ∞ における近似解を滑らかにつないだようなものになるはずだ（その際に時間座標 𝑡 の原点を適切に設定しなおす必要がある）。したがってこの解のうち膨張解は、有限の時刻に 𝑎 = 0 から始まって減速膨張し、 𝑎 = 𝑎_𝐿 になったときに加速膨張に転じ、無限の未来に 𝑎 → ∞ になる宇宙である。収縮解はその時間反転である。

解のまとめ

この節の結果をまとめると、光と物質で満たされた宇宙に対する近似的なフリードマン方程式 $$\frac{{\dot{𝑎}}^2}{{𝑎}^2}=\frac{{𝐾}_{𝑟}}{{𝑎}^4}+\frac{{𝐾}_{𝑚}}{{𝑎}^3}-\frac{𝑘}{{𝑎}^2}+\frac{𝛬}{3}({𝐾}_{𝑟}>0,{𝐾}_{𝑚}>0)\text{←}\text{(100)式}$$ の解は次のようになる。

𝛬 = 𝑘 = 0 のとき、すなわち宇宙定数が0で3次元空間部分が平坦なユークリッド空間であるときは、 𝑎 を 𝑡 の初等関数で表すことができて、解は $$𝑎=\{\begin{array}{ll}\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}\left[2\cos \right\{\frac{2}{3}\arccos (\pm \frac{3{{𝐾}_{𝑚}}^2𝑐𝑡}{4{{𝐾}_{𝑟}}^{\frac{3}{2}}})\}+1]& (\left|𝑡\right|\leqq \frac{4{{𝐾}_{𝑟}}^{\frac{3}{2}}}{3𝑐{{𝐾}_{𝑚}}^2})\\ \frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}\left[2\cosh \right\{\frac{2}{3}\mathrm{arcosh}(\pm \frac{3{{𝐾}_{𝑚}}^2𝑐𝑡}{4{{𝐾}_{𝑟}}^{\frac{3}{2}}})\}+1]& (\pm 𝑡\geqq \frac{4{{𝐾}_{𝑟}}^{\frac{3}{2}}}{3𝑐{{𝐾}_{𝑚}}^2})\end{array}\text{（複号同順）}$$ である。逆に 𝑡 を 𝑎 の関数で表せば $$\begin{array}{lll}\hfill 𝑡& =& \pm \frac{2}{3𝑐\sqrt{{𝐾}_{𝑚}}}\sqrt{𝑎+\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}}(𝑎-\frac{2{𝐾}_{𝑟}}{{𝐾}_{𝑚}})\end{array}$$ のようにいくらか簡潔になる。媒介変数表示をすれば $$\begin{array}{ll}\{\begin{array}{l}𝑡=\frac{2}{𝑐\sqrt{{𝐾}_{𝑚}}}(\frac{1}{3}{𝑢}^3-\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}𝑢)\\ 𝑎={𝑢}^2-\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}\end{array}& (\text{ただし}\left|𝑢\right|\geqq \sqrt{\frac{{𝐾}_{𝑟}}{{𝐾}_{𝑚}}})\end{array}$$ と書くこともできる。

𝛬 = 0 ≠ 𝑘 のとき、すなわち宇宙定数が0で3次元空間部分が曲がっているときは、 𝑎 を 𝑡 の初等関数で表すことはできないが、 𝑡 を 𝑎 の初等関数で表すことや便利な媒介変数表示をすることができる。解は $$\begin{array}{ll}\hfill 𝛬=0,0<𝑘\text{のとき:}& 𝑡=\pm \frac{1}{𝑐\sqrt{𝑘}}(\sqrt{\frac{-𝑘{𝑎}^2+{𝐾}_{𝑚}𝑎+{𝐾}_{𝑟}}{𝑘}}+\frac{{𝐾}_{𝑚}}{2𝑘}\arccos \frac{2𝑘𝑎-{𝐾}_{𝑚}}{\sqrt{4𝑘{𝐾}_{𝑟}+{{𝐾}_{𝑚}}^2}})\\ \hfill 𝛬=0,-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}<𝑘<0\text{のとき:}& 𝑡=\pm \frac{1}{𝑐\sqrt{-𝑘}}(\sqrt{\frac{-𝑘{𝑎}^2+{𝐾}_{𝑚}𝑎+{𝐾}_{𝑟}}{-𝑘}}+\frac{{𝐾}_{𝑚}}{2𝑘}\mathrm{arcosh}\frac{-2𝑘𝑎+{𝐾}_{𝑚}}{\sqrt{4𝑘{𝐾}_{𝑟}+{{𝐾}_{𝑚}}^2}})\\ \hfill 𝛬=0,𝑘=-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}\text{のとき:}& 𝑡=\pm \frac{1}{𝑐\sqrt{-𝑘}}\{𝑎+\frac{{𝐾}_{𝑚}}{2𝑘}\ln (𝑎-\frac{{𝐾}_{𝑚}}{2𝑘})\}\\ \hfill 𝛬=0,𝑘<-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}\text{のとき:}& 𝑡=\pm \frac{1}{𝑐\sqrt{-𝑘}}(\sqrt{\frac{-𝑘{𝑎}^2+{𝐾}_{𝑚}𝑎+{𝐾}_{𝑟}}{-𝑘}}+\frac{{𝐾}_{𝑚}}{2𝑘}\mathrm{arsinh}\frac{-2𝑘𝑎+{𝐾}_{𝑚}}{\sqrt{-4𝑘{𝐾}_{𝑟}-{{𝐾}_{𝑚}}^2}})\end{array}$$ であり、媒介変数表示をすれば $$\begin{array}{lll}\hfill 𝛬=0,0<𝑘\text{のとき:}& \{\begin{array}{l}𝑡=\frac{{𝐾}_{𝑚}}{2𝑐{𝑘}^{\frac{3}{2}}}(\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}\sin 𝑢+𝑢)\\ 𝑎=\frac{{𝐾}_{𝑚}}{2𝑘}(\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}\cos 𝑢+1)\end{array}& (\text{ただし}\left|𝑢\right|\leqq \arccos \frac{-1}{\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}})\\ \hfill 𝛬=0,-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}<𝑘<0\text{のとき:}& \{\begin{array}{l}𝑡=\frac{{𝐾}_{𝑚}}{2𝑐{(-𝑘)}^{\frac{3}{2}}}(\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}\sinh 𝑢-𝑢)\\ 𝑎=\frac{{𝐾}_{𝑚}}{-2𝑘}(\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}\cosh 𝑢-1)\end{array}& (\text{ただし}\left|𝑢\right|\geqq \mathrm{arcosh}\frac{1}{\sqrt{\frac{4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}+1}})\\ \hfill 𝛬=0,𝑘=-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}\text{のとき:}& \{\begin{array}{l}𝑡=\pm \frac{{𝐾}_{𝑚}}{2𝑐{(-𝑘)}^{\frac{3}{2}}}(\frac{-2𝑘}{{𝐾}_{𝑚}}{\mathrm{e}}^{𝑢}-𝑢)\\ 𝑎=\frac{{𝐾}_{𝑚}}{-2𝑘}(\frac{-2𝑘}{{𝐾}_{𝑚}}{\mathrm{e}}^{𝑢}-1)\end{array}& (\text{ただし}𝑢\geqq \ln \frac{{𝐾}_{𝑚}}{-2𝑘})\\ \hfill 𝛬=0,𝑘<-\frac{{{𝐾}_{𝑚}}^2}{4{𝐾}_{𝑟}}\text{のとき:}& \{\begin{array}{l}𝑡=\pm \frac{{𝐾}_{𝑚}}{2𝑐{(-𝑘)}^{\frac{3}{2}}}(\sqrt{\frac{-4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}-1}\cosh 𝑢-𝑢)\\ 𝑎=\frac{{𝐾}_{𝑚}}{-2𝑘}(\sqrt{\frac{-4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}-1}\sinh 𝑢-1)\end{array}& (\text{ただし}𝑢\geqq \mathrm{arsinh}\frac{1}{\sqrt{\frac{-4𝑘{𝐾}_{𝑟}}{{{𝐾}_{𝑚}}^2}-1}})\end{array}$$ と書くこともできる。

𝛬 ≠ 0 のとき、すなわち宇宙定数が0でないときは、 256𝛬^²𝐾_𝑟^³ − 81𝛬𝐾_𝑚^⁴ − 432𝛬𝑘𝐾_𝑟𝐾_𝑚^² − 384𝛬𝑘^²𝐾_𝑟^² + 36𝑘^³𝐾_𝑚^² + 144𝑘^⁴𝐾_𝑟 = 0 という関係式が満たされていれば 𝑡 を 𝑎 の初等関数で表すことができる。この関係式は変形すると $𝛬=3\{\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}\pm {𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\}$ と書くこともできて、解は $$\begin{array}{l}𝛬=-\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3},𝑘=-\frac{9{{𝐾}_{𝑚}}^2}{32{𝐾}_{𝑟}}\text{のとき:}𝑡=\pm \frac{1}{𝑐}\sqrt{\frac{3}{-𝛬}}(-\arccos \frac{3{𝐾}_{𝑚}𝑎-8{𝐾}_{𝑟}}{16{𝐾}_{𝑟}}+\frac{\sqrt{3}}{2}\sqrt{\frac{-{𝐾}_{𝑚}𝑎+8{𝐾}_{𝑟}}{3{𝐾}_{𝑚}𝑎+8{𝐾}_{𝑟}}})\\ 𝛬=3\{\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}-{𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\}\text{のときは𝛬の符号に応じて}\\ \begin{array}{ll}\hfill -\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3}<𝛬<0\text{のとき:}& 𝑡=\pm \frac{1}{𝑐}\sqrt{\frac{3}{-𝛬}}[-\arccos \left\{\sqrt{\frac{2𝛬𝐽}{3{𝐾}_{𝑚}}}(𝑎+𝐽)\right\}+\frac{1}{2\sqrt{1-\frac{3{𝐾}_{𝑚}}{8𝛬{𝐽}^3}}}\arccos (\sqrt{\frac{8𝛬{𝐽}^3}{3{𝐾}_{𝑚}}}\cdot \frac{𝑎+𝐽-\frac{3{𝐾}_{𝑚}}{4𝛬{𝐽}^2}}{𝑎-𝐽})]\\ \hfill 0<𝛬\text{のとき:}& 𝑡=\pm \frac{1}{𝑐}\sqrt{\frac{3}{𝛬}}[\mathrm{arcosh}\left\{\sqrt{\frac{2𝛬𝐽}{3{𝐾}_{𝑚}}}(𝑎+𝐽)\right\}-\frac{1}{2\sqrt{1-\frac{3{𝐾}_{𝑚}}{8𝛬{𝐽}^3}}}\mathrm{arcosh}(\sqrt{\frac{8𝛬{𝐽}^3}{3{𝐾}_{𝑚}}}\cdot \frac{𝑎+𝐽-\frac{3{𝐾}_{𝑚}}{4𝛬{𝐽}^2}}{|𝑎-𝐽|})]\\ \hfill \text{ただし}& 𝐽=-\frac{8{𝐾}_{𝑟}}{3{𝐾}_{𝑚}-\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}=\frac{3{𝐾}_{𝑚}+\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}{4𝑘}\end{array}\\ 𝛬=3\{\frac{27{{𝐾}_{𝑚}}^4}{512{{𝐾}_{𝑟}}^3}+\frac{9𝑘{{𝐾}_{𝑚}}^2}{32{{𝐾}_{𝑟}}^2}+\frac{{𝑘}^2}{4{𝐾}_{𝑟}}+{𝐾}_{𝑚}{(\frac{9{{𝐾}_{𝑚}}^2}{64{{𝐾}_{𝑟}}^2}+\frac{𝑘}{2{𝐾}_{𝑟}})}^{\frac{3}{2}}\}\text{のときは𝛬の符号に応じて}\\ \begin{array}{ll}\hfill -\frac{81{{𝐾}_{𝑚}}^4}{4096{{𝐾}_{𝑟}}^3}<𝛬<0\text{のとき:}& 𝑡=\pm \frac{1}{𝑐}\sqrt{\frac{3}{-𝛬}}[-\arccos \left\{\sqrt{\frac{2𝛬𝐽}{3{𝐾}_{𝑚}}}(𝑎+𝐽)\right\}+\frac{1}{2\sqrt{-1+\frac{3{𝐾}_{𝑚}}{8𝛬{𝐽}^3}}}\mathrm{arcosh}(\sqrt{\frac{8𝛬{𝐽}^3}{3{𝐾}_{𝑚}}}\cdot \frac{𝑎+𝐽-\frac{3{𝐾}_{𝑚}}{4𝛬{𝐽}^2}}{𝑎-𝐽})]\\ \hfill 0<𝛬\text{のとき:}& 𝑡=\pm \frac{1}{𝑐}\sqrt{\frac{3}{𝛬}}[\mathrm{arsinh}\left\{\sqrt{\frac{-2𝛬𝐽}{3{𝐾}_{𝑚}}}(𝑎+𝐽)\right\}-\frac{1}{2\sqrt{1-\frac{3{𝐾}_{𝑚}}{8𝛬{𝐽}^3}}}\mathrm{arsinh}(\sqrt{\frac{-8𝛬{𝐽}^3}{3{𝐾}_{𝑚}}}\cdot \frac{𝑎+𝐽-\frac{3{𝐾}_{𝑚}}{4𝛬{𝐽}^2}}{𝑎-𝐽})]\\ \hfill \text{ただし}& 𝐽=-\frac{8{𝐾}_{𝑟}}{3{𝐾}_{𝑚}+\sqrt{9{{𝐾}_{𝑚}}^2+32𝑘{𝐾}_{𝑟}}}\end{array}\end{array}$$ である。これらの 𝐽 はいずれの場合も $$𝐽=-\frac{4{𝐾}_{𝑟}(9𝛬{{𝐾}_{𝑚}}^2+8𝛬𝑘{𝐾}_{𝑟}-6{𝑘}^3)}{3{𝐾}_{𝑚}(9𝛬{{𝐾}_{𝑚}}^2+16𝛬𝑘{𝐾}_{𝑟}-4{𝑘}^3)}=-\frac{3{𝐾}_{𝑚}(4𝛬{𝐾}_{𝑟}+{𝑘}^2)}{9𝛬{{𝐾}_{𝑚}}^2+8𝛬𝑘{𝐾}_{𝑟}-6{𝑘}^3}$$ という共通の表式で書くこともできる。

この他に特別な条件が満たされているときに 𝑡 を 𝑎 の初等関数で表すことができる場合があるが、実用的でないので割愛する。

初等関数で表される解は以上だ。