「双子のパラドックス」を両者の視点から計算する。

相対性理論におけるいわゆる「双子のパラドックス」について、定性的な説明は世の中いたるところにある。定量的に両者の経過時間を計算している説明もあるが、待っている慣性系側の視点のみで計算したものや、加減速時を無視して等速直線運動するところだけ計算したものなど、サボっているものが多い。
ここでは加減速時も含めて両者の視点から定量的な計算を行う。
少しずつ記事を増やしていきます。


相対性理論におけるいわゆる「双子のパラドックス」について、定性的な説明は世の中いたるところにある。定量的に両者の経過時間を計算している説明もあるが、待っている慣性系側の視点のみで計算したものや、加減速時を無視して等速直線運動するところだけ計算したものなど、サボっているものが多い。
ここでは加減速時も含めて両者の視点から定量的な計算を行う。
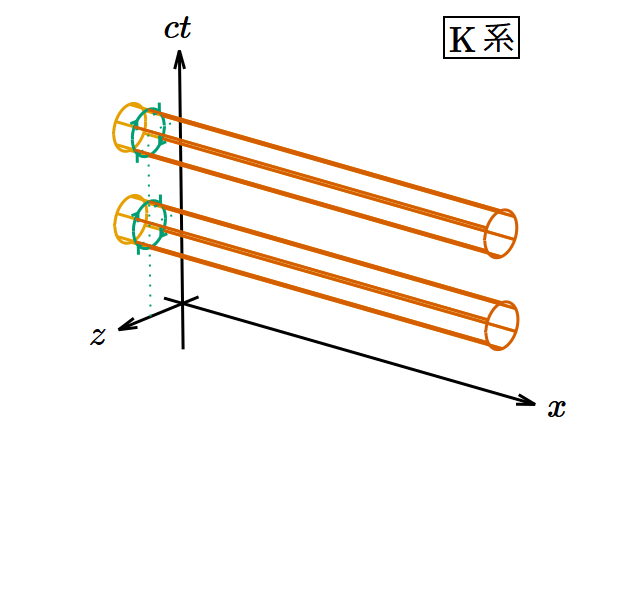
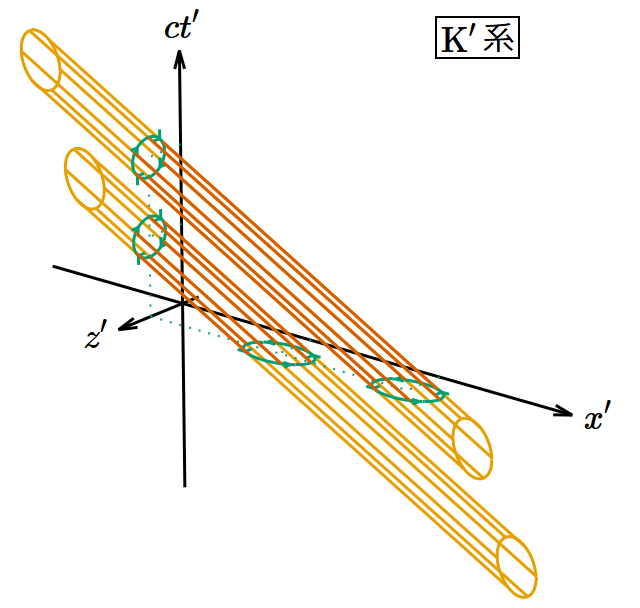
電磁場をローレンツ変換すると、電場と磁場が混じり合う。その変換は数式ではっきり示されており、何ら曖昧なところはない。
だが、上向きの電場中で観測者が前進すると左向きの磁場が生じる、などと言われてもどういうからくりになっているのか直感的に理解しがたい。このような状況をすんなり納得できるような、幾何学的なモデルを作ってみよう。
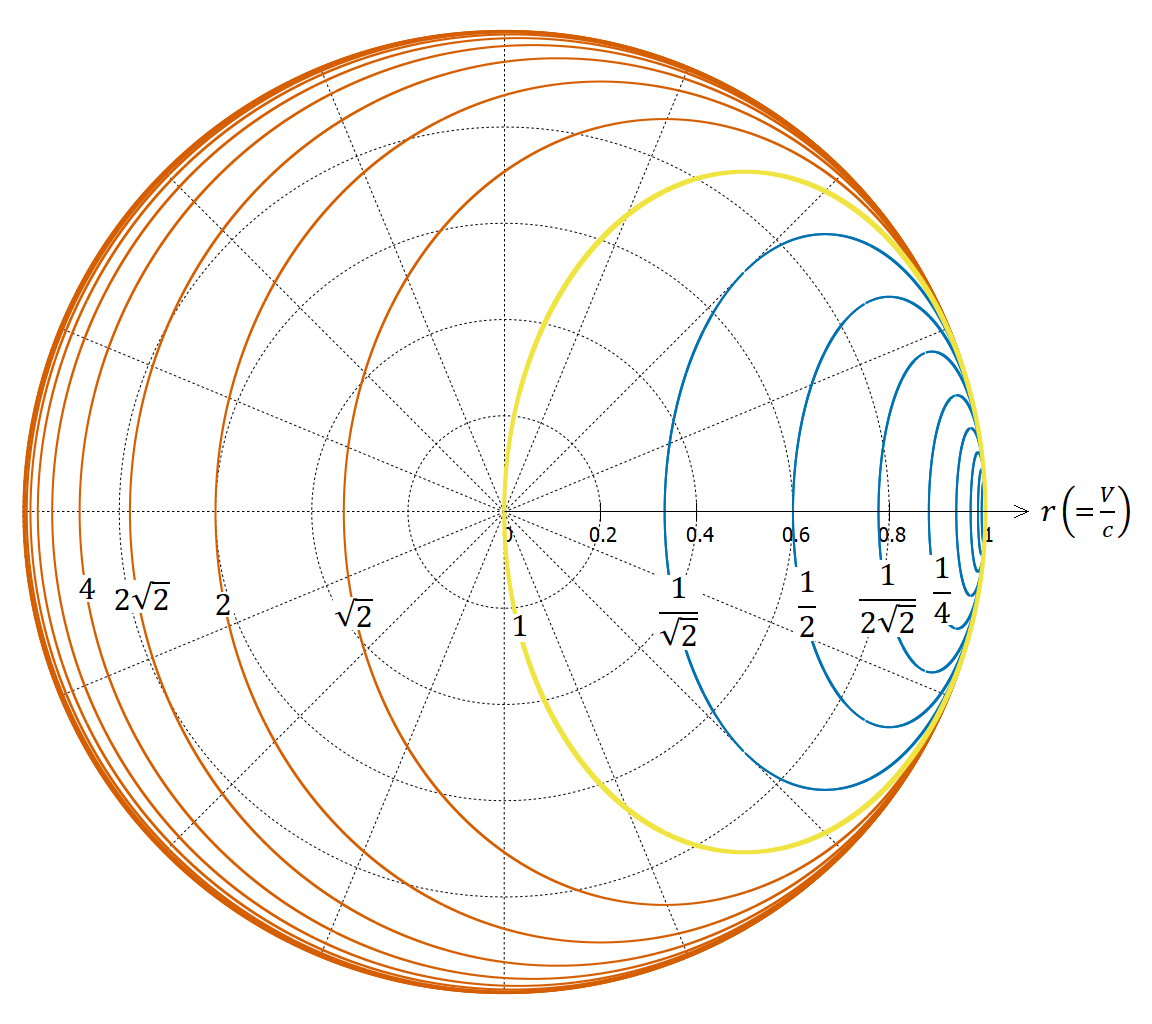
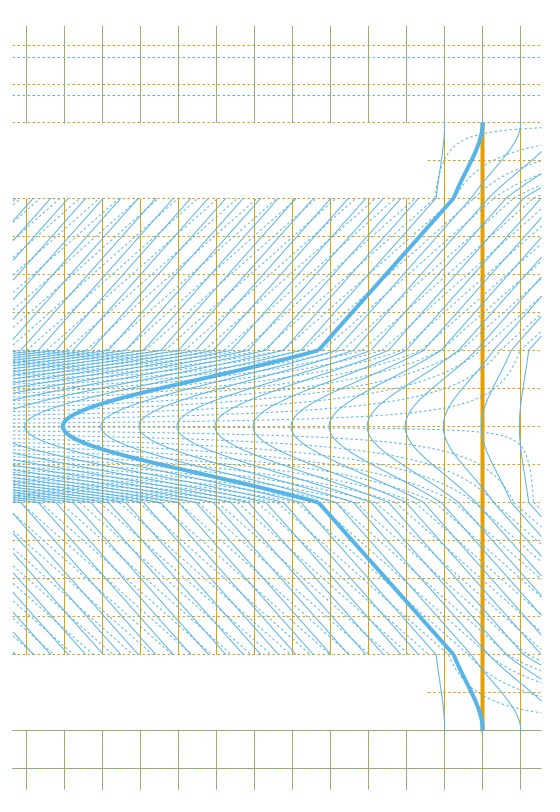
相対論的な速度における光のドップラー効果では、非相対論的なドップラー効果にはないような現象が現れる。
光源が斜めに動いたとき、その方向と速さに応じてどれだけ波長(または振動数)が変わるか計算してみよう。
重力場の方程式(アインシュタイン方程式)の自明でない厳密解のうち、もっとも単純と考えられる球対称の解を求める。
重力場の方程式の解のうち、球対称・定常・真空の解であるシュバルツシルト解(外部解)を導出する。
重力場の方程式の解のうち、球対称・定常・一様密度・完全流体の解であるシュバルツシルト解(内部解)を導出する。
シュバルツシルト解(外部解・内部解)を拡張し、天体が球対称・定常・完全流体であるが密度が一様でない場合でも適用できる解を導出する。
シュバルツシルト解(外部解)の条件を緩めて、「定常」の条件を取っ払って時間変化しても構わないことにすればどんな解が得られるだろうか、計算してみよう。
球対称・定常で電荷を伴った解であるライスナー・ノルドシュトルム解を導出する。ついでに、定常に限らないときのことも考える。
宇宙項を考慮したらシュバルツシルト解はどう変わるのだろうか。「厳密解」というからには宇宙項が厳密にはどのように解に影響するのか知りたくなる。それを計算してみよう。
シュバルツシルト解(外部解)のリッチテンソルはゼロであるが、リーマンテンソルはゼロではない。ではリーマンテンソルの値はどうなっているのか、そのすべての成分を計算してみよう。
ついでにシュバルツシルト解(内部解)のリーマンテンソルとリッチテンソルも計算しておく。
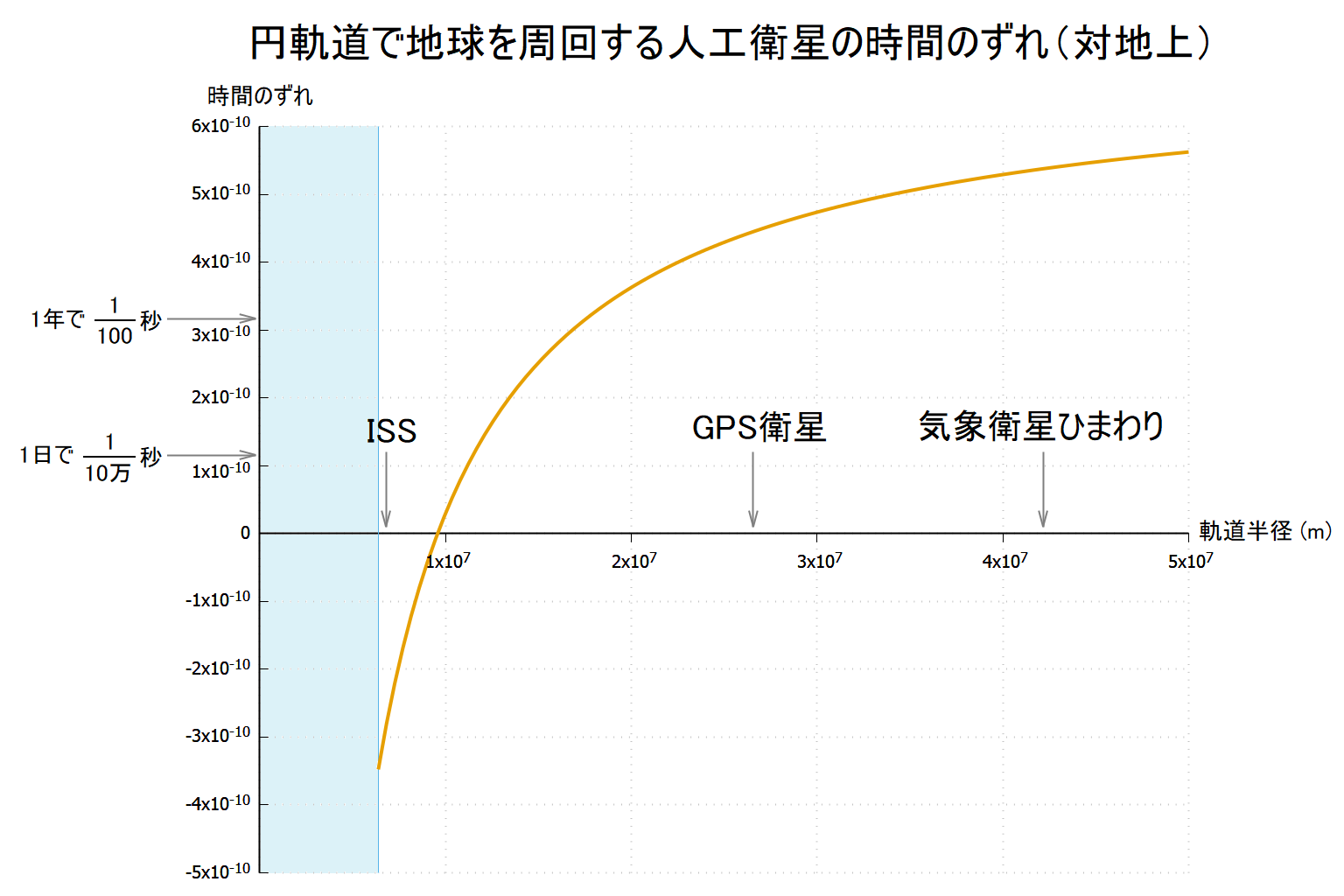
地球を周回する人工衛星の時間は、地上の時間からずれる。
そのずれを計算する方法は主に2つある。1つ目の方法は、人工衛星が動いているために生じる時間の遅れと、人工衛星が高いところに位置しているために生じる時間の進みを、別々に算出して足す方法である。2つ目の方法は、重力場の方程式の解を使ってまとめて一気に計算する方法である。
ここでは円軌道の人工衛星に対して両方のやり方で計算し、両者が同じ結果になることを示す。
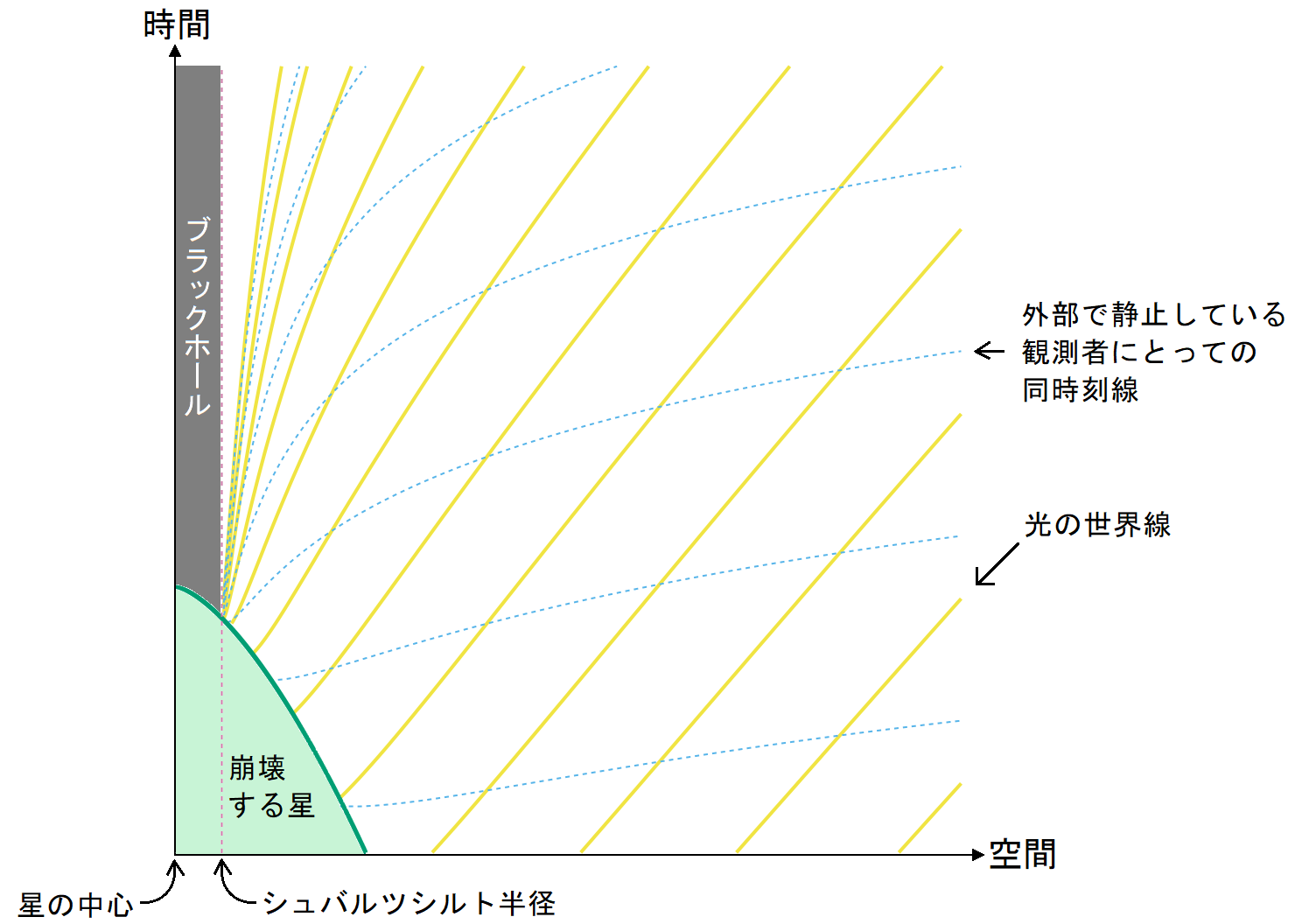
なぜブラックホールは見えないのだろうか。それはたいてい、ブラックホールの重力がとても強いので光もブラックホールに引かれて外に出られないからだ、といったように説明される。確かに重力のせいでブラックホールからは光もまったく出てこないし、光が出てこなければ見えないのは当たり前なので、そこは間違っていない。しかしこの説明だけでは状況を正しく思い浮かべることは難しく、誤解を招くようにも思える。
ここでは一般相対性理論で説明されるブラックホールがどういう構造になっているから見えないのかを簡単に述べる。
一様・等方な宇宙全体が満たすべき重力場の方程式がどのような形になるか、そこからどのような解が得られるかを考える。
一様・等方な時空を表す計量を考え、その計量に対して重力場の方程式を適用し、フリードマン方程式を導出する。
エネルギーや圧力が0である真空の条件でフリードマン方程式の厳密解を求める。
一様に光や物質で満たされているような宇宙に対して、状態方程式の具体的な形を仮定してフリードマン方程式の解を求める。
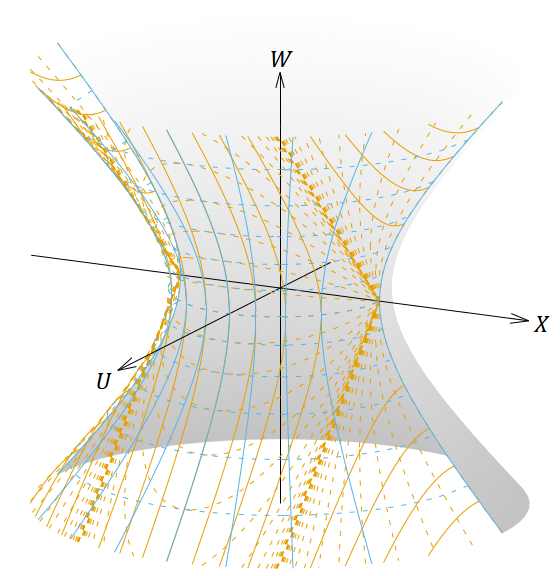
普通の光や物質がまったく存在しない真空という条件でフリードマン方程式を解くと、宇宙定数の符号と3次元空間の曲率の符号に応じて異なる形の解が出てくる。これらの解で表される時空がどのような形をしているのかを考えてみると、いくつかの解は座標変換すれば同じものを表していて、解の種類は見た目ほど多くないことがわかる。
そしてこれらの解である4次元時空は平坦な5次元時空に埋め込むことができて、その4次元超曲面は単純な式で表すことができる。
参考にした文献を挙げる。 ➜ 参考文献に進む